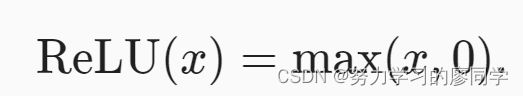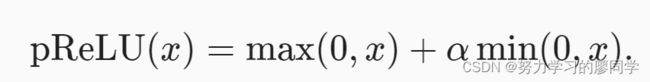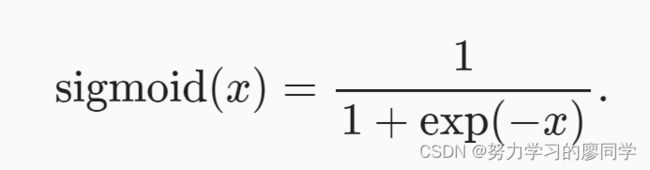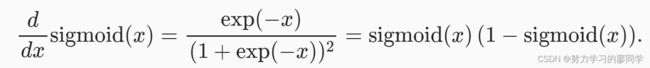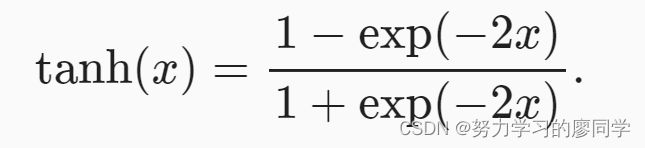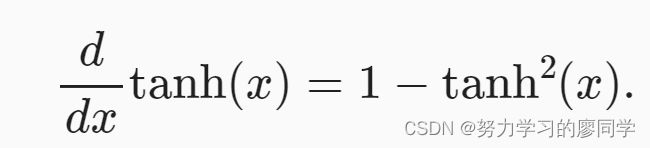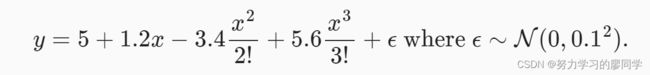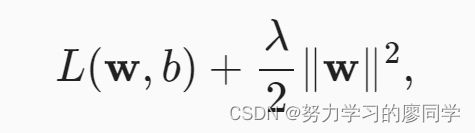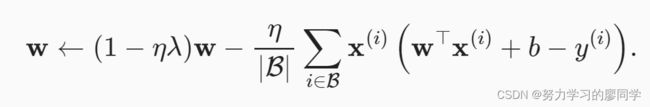动手学深度学习笔记day5

多层感知机

1、模型输出并不是和每一个特征都是线性相关的，在特征之间的右复杂的相关交互作用。

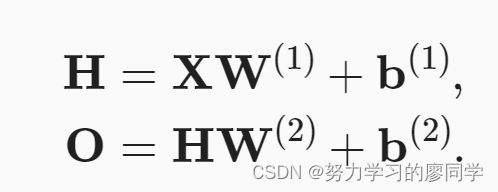
2、每一层都输出到上面的层，直到生成最后的输出。 我们可以把前L−1层看作表示，把最后一层看作线性预测器。 这种架构通常称为多层感知机（multilayer perceptron），通常缩写为MLP。

多层感知机中的层数为隐藏层和输出层。（不包含输入层）。

 没有加激活函数的话，仿射函数的仿射函数本身就是仿射函数，我们没有好处！

3、在仿射变换之后对每个隐藏单元应用非线性的激活函数（activation function）σ。 激活函数的输出（例如，σ(⋅)）被称为活性值（activations）。 一般来说，有了激活函数，就不可能再将我们的多层感知机退化成线性模型。

激活函数

ReLU函数

给定元素x，ReLU函数被定义为该元素与0的最大值。ReLU函数通过将相应的活性值设为0，仅保留正元素并丢弃所有负元素。

 当输入为负时，ReLU函数的导数为0，而当输入为正时，ReLU函数的导数为1。 注意，当输入值精确等于0时，ReLU函数不可导。

使用ReLU的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。 这使得优化表现得更好，并且ReLU减轻了困扰以往神经网络的梯度消失问题。

ReLU函数变体：参数化pReLU

ReLU函数有许多变体，包括参数化ReLU（Parameterized ReLU，） 函数。 该变体为ReLU添加了一个线性项，因此即使参数是负的，某些信息仍然可以通过：

sigmoid函数

 对于一个定义域在R中的输入， sigmoid函数将输入变换为区间(0, 1)上的输出。 因此，sigmoid通常称为挤压函数（squashing function）： 它将范围（-inf, inf）中的任意输入压缩到区间（0, 1）中的某个值：

sigmoid函数的导数为下面的公式。当输入为0时，sigmoid函数的导数达到最大值0.25； 而输入在任一方向上越远离0点时，导数越接近0。

 

  tanh函数

 tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。 tanh函数的公式如下。

 tanh函数的导数为下面的公式。当输入接近0时，tanh函数的导数接近最大值1。 与我们在sigmoid函数图像中看到的类似， 输入在任一方向上越远离0点，导数越接近0。

 多层感知机的从零开始实现

import torch
from torch import nn
from d2l import torch as d2l

#1、继续使用Fashion-MNIST图像分类数据集 
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)  #上一节已经定义的函数

#2、 初始化模型参数
#将每个图像视为具有784个输入特征 和10个类的简单分类数据集。 多层感知机包含256个隐藏单元。

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

#3、ReLU激活函数
def relu(X):
    a = torch.zeros_like(X)  #定义一个和x形状一样的全零矩阵
    return torch.max(X, a)

#4、模型
#使用reshape将每个二维图像转换为一个长度为num_inputs的向量
def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # 这里“@”代表矩阵乘法
    return (H@W2 + b2)

#5、损失函数
#直接使用高级API中的内置函数来计算softmax和交叉熵损失。
loss = nn.CrossEntropyLoss(reduction='none')

#6、训练
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater) #上一节已经定义的函数

#7、测试
d2l.predict_ch3(net, test_iter)

多层感知机的简洁实现

import torch
from torch import nn
from d2l import torch as d2l

#1、模型
net = nn.Sequential(nn.Flatten(),  #输入为一批数据，第一维为batch，通常要把一个数据拉成一维，而#不是将一批数据拉为一维。所以torch.nn.Flatten()默认从第二维开始平坦化。
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);  #在网络模型中运用初始化w，假如该层模型是nn.Linear，jiu进行初始化


batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

模型选择（过拟合与欠拟合）

评估几个候选模型后选择最终的模型。 这个过程叫做模型选择

将模型在训练数据上拟合的比在潜在分布中更接近的现象称为过拟合（overfitting）， 用于对抗过拟合的技术称为正则化（regularization）。

训练误差和泛化误差

 训练误差（training error）是指， 模型在训练数据集上计算得到的误差。

 泛化误差（generalization error）是指， 模型应用在同样从原始样本的分布中抽取的无限多数据样本时，模型误差的期望。

我们永远不能准确地计算出泛化误差。 这是因为无限多的数据样本是一个虚构的对象。 在实际中，我们只能通过将模型应用于一个独立的测试集来估计泛化误差， 该测试集由随机选取的、未曾在训练集中出现的数据样本构成。

影响模型泛化的因素：

1、可调整参数的数量。当可调整参数的数量（也称为自由度）很大时，模型往往更容易过拟合。2、参数采用的值。当权重的取值范围较大时，模型可能更容易过拟合。

3、训练样本的数量。即使你的模型很简单，也很容易过拟合只包含一两个样本的数据集。而过拟合一个有数百万个样本的数据集则需要一个极其灵活的模型。

验证集

 除了训练和测试数据集之外，还增加一个验证数据集（validation dataset）， 也叫验证集（validation set）。

K折交叉验证

原始训练数据被分成K个不重叠的子集。 然后执行K次模型训练和验证，每次在K−1个子集上进行训练， 并在剩余的一个子集（在该轮中没有用于训练的子集）上进行验证。 最后，通过对K次实验的结果取平均来估计训练和验证误差。

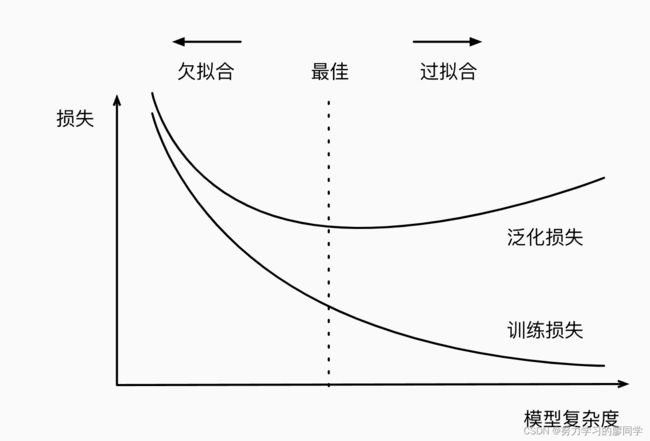
欠拟合和过拟合

 如果模型不能降低训练误差，这可能意味着模型过于简单。 这种现象被称为欠拟合（underfitting）。

当我们的训练误差明显低于验证误差时要小心， 这表明严重的过拟合（overfitting）。

 多项式回归模拟欠拟合与过拟合

import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l


#1、生成数据集
max_degree = 20  # 多项式的最大阶数
n_train, n_test = 100, 100  # 训练和测试数据集大小
true_w = np.zeros(max_degree)  # 分配大量的空间
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])

features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1)) 
#[200,],[1,20]->[200,20]
for i in range(max_degree):
    poly_features[:, i] /= math.gamma(i + 1)  # gamma(n)=(n-1)!
# labels的维度:(n_train+n_test,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)

# NumPy ndarray转换为tensor
true_w, features, poly_features, labels = [torch.tensor(x, dtype=
    torch.float32) for x in [true_w, features, poly_features, labels]]


#2、对模型进行训练和测试
def evaluate_loss(net, data_iter, loss):  #@save
    """评估给定数据集上模型的损失"""
    metric = d2l.Accumulator(2)  # 损失的总和,样本数量
    for X, y in data_iter:
        out = net(X)
        y = y.reshape(out.shape)
        l = loss(out, y)
        metric.add(l.sum(), l.numel())
    return metric[0] / metric[1]


def train(train_features, test_features, train_labels, test_labels,
          num_epochs=400):
    loss = nn.MSELoss(reduction='none')
    input_shape = train_features.shape[-1]
    # 不设置偏置，因为我们已经在多项式中实现了它
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
    batch_size = min(10, train_labels.shape[0])
    train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
                                batch_size)
    test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
                               batch_size, is_train=False)
    trainer = torch.optim.SGD(net.parameters(), lr=0.01)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
                            xlim=[1, num_epochs], ylim=[1e-3, 1e2],
                            legend=['train', 'test'])
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
                                     evaluate_loss(net, test_iter, loss)))
    print('weight:', net[0].weight.data.numpy())


#3、三阶多项式函数拟合(正常)
# 从多项式特征中选择前4个维度，即1,x,x^2/2!,x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
      labels[:n_train], labels[n_train:])
#weight: [[ 5.019018   1.1946101 -3.4238737  5.6215625]]

#4、线性函数拟合(欠拟合)
# 从多项式特征中选择前2个维度，即1和x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
      labels[:n_train], labels[n_train:])
#weight: [[3.643353  3.9591959]]


#5、高阶多项式函数拟合(过拟合)
# 从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:, :],
      labels[:n_train], labels[n_train:], num_epochs=1500)

#weight: [[ 4.98981619e+00  1.28851151e+00 -3.28302407e+00  5.15355873e+00
  -3.46124321e-01  1.13549972e+00  5.10900607e-03  1.18201613e-01
  -1.63049936e-01 -1.38878882e-01  2.88553052e-02 -1.50383292e-02
  -1.69221520e-01 -1.03751056e-01  8.86610001e-02  5.50406016e-02
  -1.06619544e-01  3.09333988e-02  1.18263520e-01 -1.75979659e-01]]

缓解过拟合

权重衰减

权重衰减（weight decay）是最广泛使用的正则化的技术之一， 它通常也被称为L2正则化。

要保证权重向量比较小， 最常用方法是将其范数作为惩罚项加到最小化损失的问题中。 将原来的训练目标最小化训练标签上的预测损失， 调整为最小化预测损失和惩罚项之和。 现在，如果我们的权重向量增长的太大， 我们的学习算法可能会更集中于最小化权重范数‖w‖2。 这正是我们想要的。loss如下

  L2正则化回归的小批量随机梯度下降更新如下式：

 我们根据估计值与观测值之间的差异来更新w。 然而，我们同时也在试图将w的大小缩小到零。

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2

 l = loss(net(X), y) + lambd * l2_penalty(w)

暂退法（Dropout）

泛化性和灵活性之间的这种基本权衡被描述为偏差-方差权衡（bias-variance tradeoff）。 线性模型有很高的偏差：它们只能表示一小类函数。 然而，这些模型的方差很低：它们在不同的随机数据样本上可以得出相似的结果。

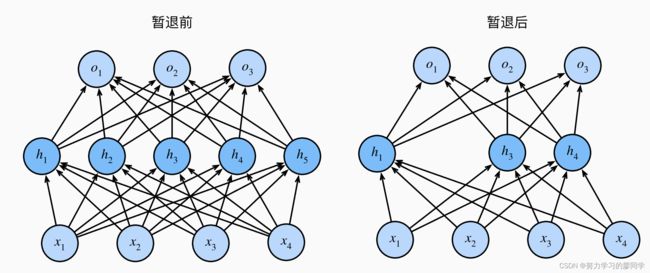
暂退法在前向传播过程中，计算每一内部层的同时注入噪声，因为我们从表面上看是在训练过程中丢弃（drop out）一些神经元。 在整个训练过程的每一次迭代中，标准暂退法包括在计算下一层之前将当前层中的一些节点置零。

 在每次训练迭代中，他将从均值为零的分布ϵ∼N(0,σ2) 采样噪声添加到输入x， 从而产生扰动点x′=x+ϵ， 预期是E[x′]=x。每个中间活性值h以暂退概率p由随机变量h′替换，如下所示：

 根据此模型的设计，其期望值保持不变，即E[h′]=h。

 从零开始实现

要实现单层的暂退法函数， 我们从均匀分布U[0,1]中抽取样本，样本数与这层神经网络的维度一致。 然后我们保留那些对应样本大于p的节点，把剩下的丢弃。

在下面的代码中，我们实现 dropout_layer 函数， 该函数以dropout的概率丢弃张量输入X中的元素， 如上所述重新缩放剩余部分：将剩余部分除以1.0-dropout。

import torch
from torch import nn
from d2l import torch as d2l


def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

#1.定义模型参数
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

#2.定义模型
#可以为每一层分别设置暂退概率： 常见的技巧是在靠近输入层的地方设置较低的暂退概率。
dropout1, dropout2 = 0.2, 0.5

class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training = True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()

    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
        # 只有在训练模型时才使用dropout
        if self.training == True:
            # 在第一个全连接层之后添加一个dropout层
            H1 = dropout_layer(H1, dropout1)
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            # 在第二个全连接层之后添加一个dropout层
            H2 = dropout_layer(H2, dropout2)
        out = self.lin3(H2)
        return out


net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

#3、训练和测试
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

简洁实现

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

动手学深度学习在线课程