定点量化误差python仿真.零极点(1)

在算法仿真中，由于是全精度的计算，曲线往往比较理想。但在把算法写入硬件时，由于资源限制，必须要进行量化。由此带来的误差，将在本节用零极点，以及下一节用频率响应进行演示。

系统为二阶的数字滤波器，方程为：

H(z) = b / a

其中，b = 0.05，a = 1 + 1.7*z^-1 + 0.745*z^-2

N为量化位数，可以任意设置。N越多，误差越小，当然消耗的硬件资源也会随之增加。

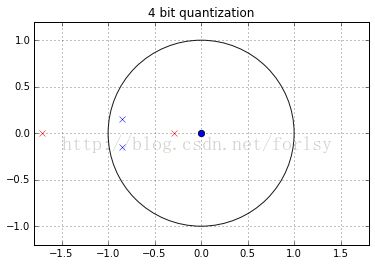
下面是量化bit为4位和8位时的情况。可以看到，当量化bit为4时，系统严重失真。极点跑到了单位圆外面，导致频率响应不存在了；而8bit量化时，量化后的性能接近量化前的理想情况。

代码如下：

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
from matplotlib.patches import Circle

N = 8          # quantization bits
Fs = 1000       # sampling frequency
a = np.array([1, 1.7, 0.745])      # denominator
b = np.array([0.05, 0, 0])         # numerator

# z zero, p pole, k gain
z1, p1, k1 = signal.tf2zpk(b,a)     # zero, pole and gain

c = np.vstack((a,b))
Max = (abs(c)).max()        #find the largest value
a = a / Max             #normalization
b = b / Max

Ra = (a * (2**((N-1)-1))).astype(int)   # quantizan and truncate
Rb = (b * (2**((N-1)-1))).astype(int)
z2, p2, k2 = signal.tf2zpk(Rb,Ra)

fig, ax = plt.subplots()
circle = Circle(xy = (0.0, 0.0), radius = 1, alpha = 0.9, facecolor = 'white')
ax.add_patch(circle)
for i in p1:
    ax.plot(np.real(i),np.imag(i), 'bx')    #pole before quantization
for i in z1:
    ax.plot(np.real(i),np.imag(i),'bo')     #zero before quantization
for i in p2:
    ax.plot(np.real(i),np.imag(i), 'rx')    #pole after quantization
for i in z2:
    ax.plot(np.real(i),np.imag(i),'ro')     #zero after quantization

 
ax.set_xlim(-1.8,1.8)
ax.set_ylim(-1.2,1.2)    
ax.grid()
ax.set_title("%d bit quantization" %N)  
plt.show()