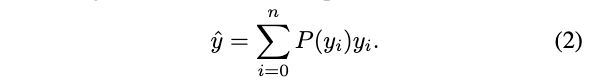GFLV2：边界框不确定性的进一步融合，提点神器 | CVPR 2021

  GFLV2基于GFLV1的bbox分布进行改进，将分布的统计信息融入到定位质量估计中，整体思想十分创新和完备，从实验结果来看，效果还是挺不错的

来源：晓飞的算法工程笔记 公众号

论文: Generalized Focal Loss V2: Learning Reliable Localization Quality Estimationfor Dense Object Detection

• 论文地址：https://arxiv.org/abs/2011.12885
• 论文代码：https://github.com/implus/GFocalV2

Introduction

---

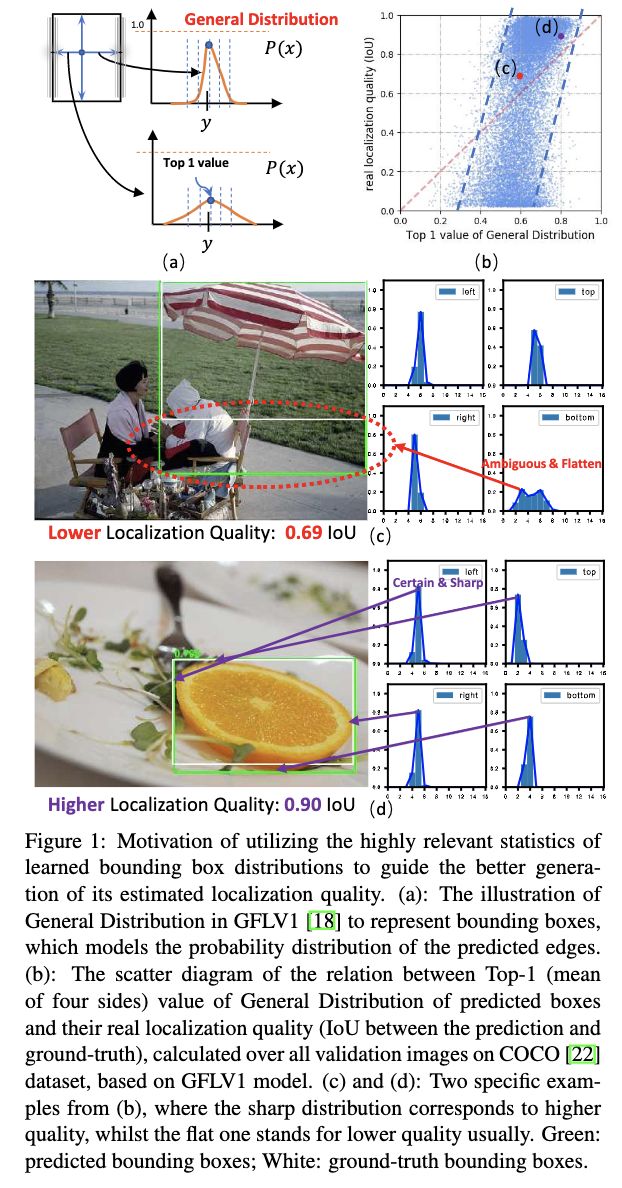
  GFL系列方法将bbox的四个值预测转化为四个分布预测，能够在输出预测值的同时根据分布判断预测值的预测可靠性。如图1c和图1d所示，高可靠性的预测结果的分布较为集中，低可靠性的预测结果的分布则较为分散。另外，论文将GFL的每个bbox的四个分布的最大值的均值与实际的IoU进行了对比，发现有较高的关联性，表明GFL的分布预测效果还是不错的。

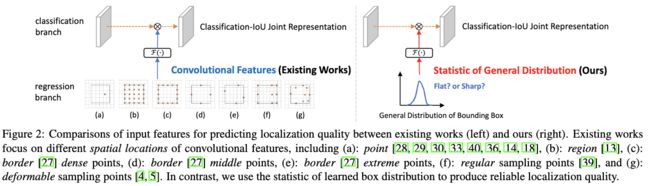
  在当前的目标检测算法中，定位质量(Localization Quality Estimation, LQE)越来越得到重视。LQE不仅能够帮助留下高质量的预测框，还可以避免NMS的误消除。之前的方法大都从卷积特征直接进行LQE，如图2左所示，主要是特征采用上做文章，但实际上这些采样的特征更多是跟分类相关的。如前面所述，GFL预测的bbox分布信息与实际IoU有较强的关联性，于是论文将其融入LQE中，提出了GFLV2，如图2右所示。
  论文的主要贡献如下：

• 首次将bbox分布信息融入到定位质量预测中进行端到端的目标检测。
• GFLV2整体架构轻量且消耗极少，能够嵌入到其它框架中带了～2AP的提升。
• GFLV2在COCO中达到了53.3AP。

Generalized Focal Loss V1

---

  讲GFLV2前先概括地总结一下GFLV1，主要有两点，分别是Classification-IoU Joint Representation以及General Distribution of Bounding Box Representation，具体可以看Generalized Focal Loss：Focal loss魔改以及预测框概率分布，保涨点 | NeurIPS 2020。

Classification-IoU Joint Representation

  这一块是GFLV1的其中一个核心，初衷是将解决训练和推理过程定位质量预测和分类预测不一致的问题(训练时分开训练，推理时却合并输出)，简单点说就是直接将分类分支的输出改为IoU和分类的合并结果$J=[J_1,J_2,\cdots ,J_m]$：

  公式1将原本的离散的训练目标转成了连续的目标，为了更好的进行训练，论文也将原本用于离散值的Focal loss修改成用于连续值的Focal loss。

General Distribution of Bounding Box Representation

  GFLV1的另一个核心是将直接预测bbox的四个值改为预测bbox的四个分布$P(x)$，bbox的每条边的预测值可通过预设区域$[y_0,y_n]$的积分$\hat{y}={\int }_{-\infty }^{+\infty }P(x)xdx={\int }_{y_0}^{y_n}P(x)xdx$获得。为了完成分布的预测，将网络的输出变为$n$个离散值，给定离散分布特性${\sum }_{i=0}^{n}P(y_i)=1$，回归值$\hat{y}$的计算为：

  相对于直接预测值，分布$P(x)$还能反应预测值的可靠性。为了网络能够更好地学习预测的分布，论文还提出了针对分布学习的损失函数进行引导。

Generalized Focal Loss V2

---

Decomposed Classification-IoU Representation

  GFLV1虽然解决了训练和推理过程定位质量预测和分类预测不一致的问题，但仅用分类分支进行联合概率的预测依然有其局限性，所以GFLV2直接融合了分类$C$和回归$I$分支：

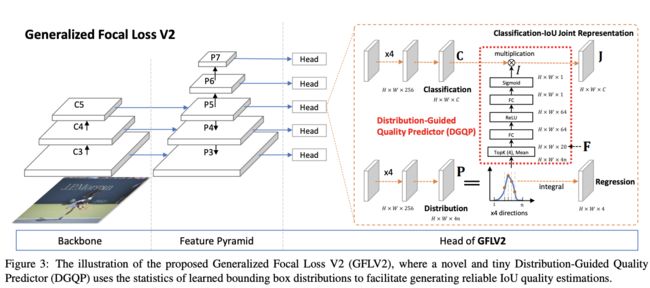
  $C=[C_1,C_2,\cdots ,C_m]$,$C_i\in [0,1]$为$m$个类别的分类特征，$I\in [0,1]$为IoU特征的标量。尽管$J$被分解成了两个部分，但由于在训练和推理阶段都直接使用，依然可以避免不一致的问题。在计算时，先将分类分支的$C$和回归分支经过Distribution-Guided Quality Predictor(DGQP)得到的$I$进行结合，训练时使用GFLV1提出的QFL进行监督训练，推理时直接将联合结果用于NMS中。

Distribution-Guided Quality Predictor

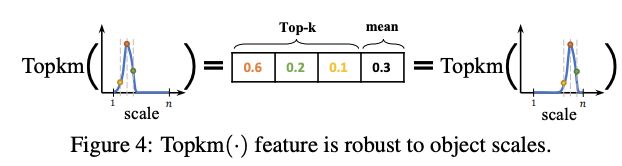
  DGQP是GFLV2的核心组件，通过小的子网将预测的分布$P$的统计信息转化为IoU标量$I$，用于生成分类-IoU联合特征。跟GFLV1一样，将每条边的相对距离$\{l,r,t,b\}$作为回归目标，每个bbox生成对应四个离散的分布$P^w=[P^w(y_0),P^w(y_1),\cdots ,P^w(y_n)]$，$w\in l,r,t,b$。如图1所示，分布$P$的平坦情况能够反映bbox的质量，在实际计算中，论文选择概率分布$P^w$的Top-k值及其均值，concatenate后作为基础的统计特征$F\in {\mathbb{R}}^{4(k+1)}$：

  选择Top-k值和均值有两个好处：

• 由于$P^w$的和固定为1，Top-k值和均值能够更好地反映分布的平坦情况，比如值越大越尖，值越小则越平。

• Top-k值和均值能够使得统计特征对分布区域上的相对偏移不敏感，生成与目标尺寸无关的鲁棒特征。

  给定统计特征$F$作为输入，使用小型子网$\mathcal{F}(\cdot )$进行IoU质量预测，子网主要由两层全连接层构成，分别接ReLU和Sigmoid激活，IoU标量$I$的计算为：

  $W_1\in {\mathbb{R}}^{p\times 4(k+1)}$,$W_1\in {\mathbb{R}}^{1\times p}$，$p$为channel维度。由于DGQP的结构十分轻量，所以几乎不会对原本的训练和推理造成过多的额外开销。

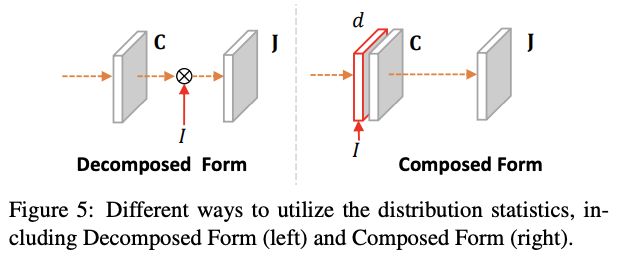
  论文也尝试用DFQP生成额外的特征与分类特征进行contatenate，然后再后续操作，但效果没有直接融合好，具体可以看看实验部分。

Experiment

---

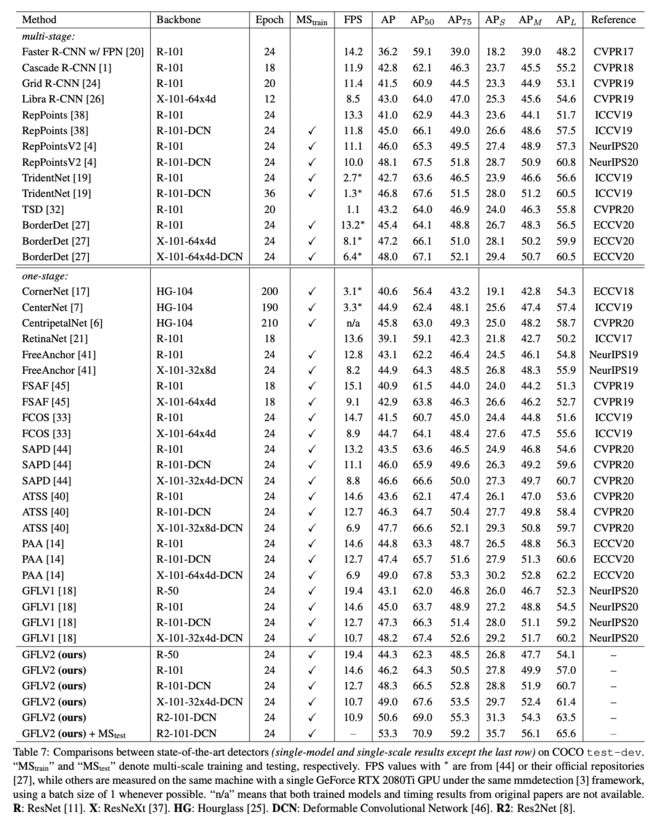
  从整体结果来看，GFLV2在准确率和速度上都有不错的表现，论文还有很多丰富的对比实验，有兴趣的可以去看看原文。

Conclusion

---

  GFLV2基于GFLV1的bbox分布进行改进，将分布的统计信息融入到定位质量估计中，整体思想十分创新和完备，从实验结果来看，效果还是挺不错的。

 
 
 

如果本文对你有帮助，麻烦点个赞或在看呗～
更多内容请关注 微信公众号【晓飞的算法工程笔记】