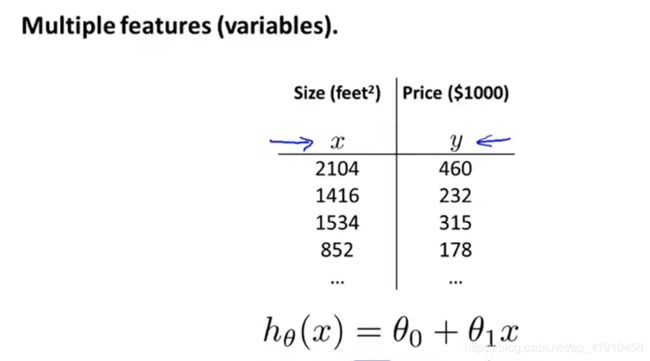
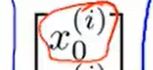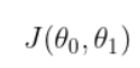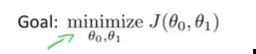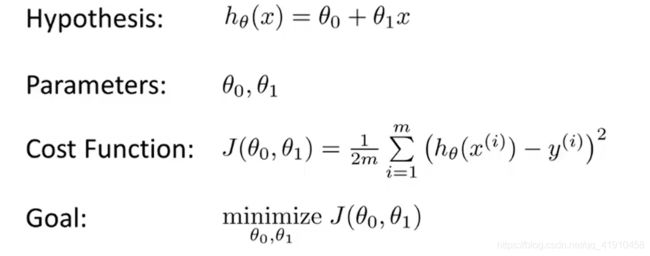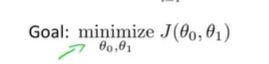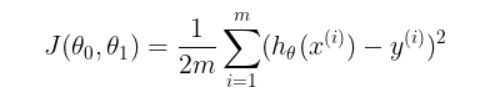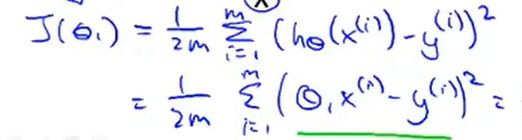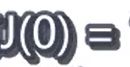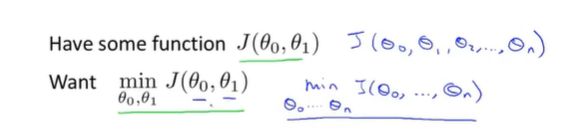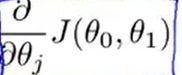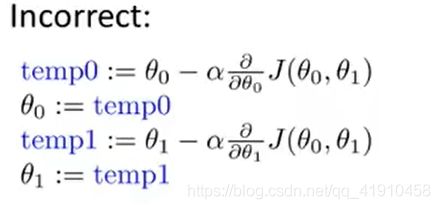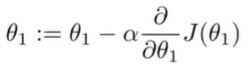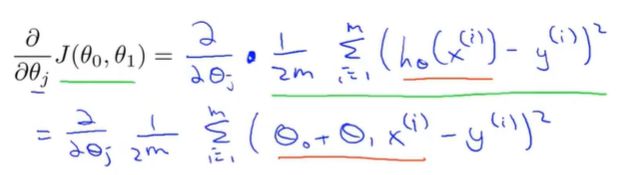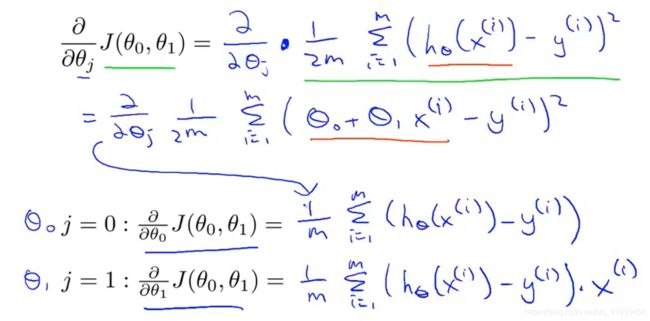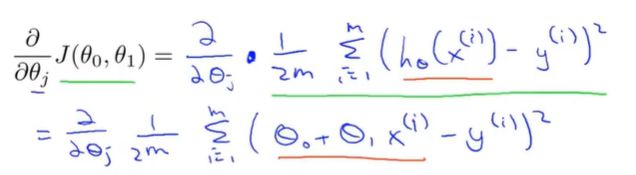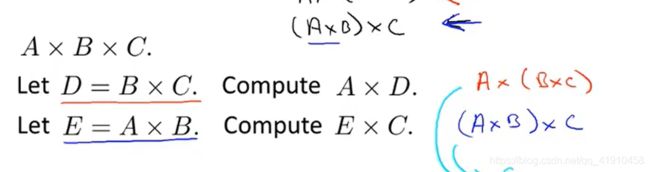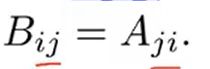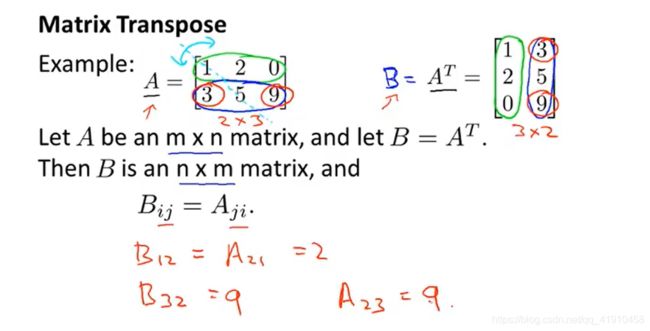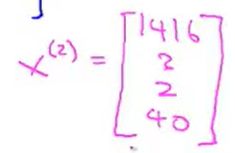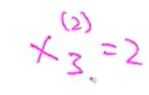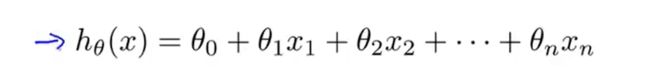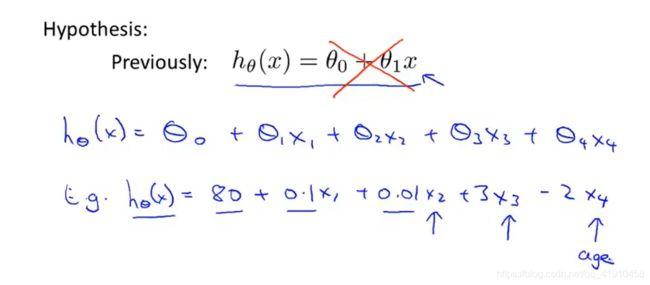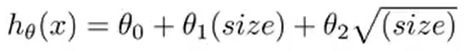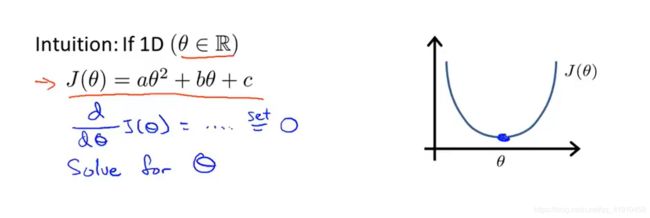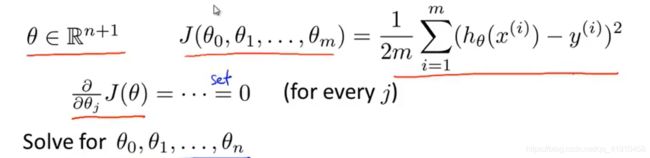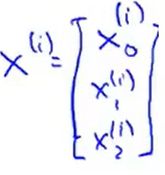吴恩达机器学习课程笔记(英文授课) Lv.1 新手村(回归)
目录
1-1机器学习的相关名词
1-2 什么是机器学习?
1.definition 定义
2.主要的机器学习算法的分类
1-3有监督学习及常用算法
1.定义
2.两种数据类型补充:categorical data离散(分类型)数据与numerical data连续(数值型)数据
3.有监督学习与回归问题、分类问题的关系
1-4无监督学习
1.定义
2.无监督学习之聚类算法的现实应用
2-1第一个学习算法—线性回归算法
1. 课程中符号的表示:
2.监督学习算法的工作过程以及线性回归模型的介绍(单变量)
2-2代价函数|平方误差函数|平方误差代价函数(取决于误差项的平方和)
2-3代价函数(一)简单了解代价函数原理
2-4代价函数(二)深入理解
2-5 梯度下降 Gradient descent (同步更新参数)
2-6 梯度下降知识点总结
2-7线性回归的梯度下降(迭代算法)
3.矩阵与向量知识
1.矩阵和向量(Matrices and vectors)
2.加法与标量乘法
3.矩阵向量乘法
4.矩阵乘法
5.矩阵乘法的特征
6.矩阵的逆运算与转置(与实数运算区别)
4-1多元线性回归
4-2多元梯度下降法
4-3 多元梯度下降法演练——特征缩放
4-4多元梯度下降法Ⅱ---学习率
4-5 特征和多项式回归 (对单特征的分析?哪些适合来进行预测?)
4-6 正规方程(区别于迭代方法的直接解法)Normal equation 求代价函数最优参数θ
4-7 正规方程在矩阵不可逆情况下的解决方法(进阶版 选学)很少发生
补充:5-6⭐矢量化实现线性回归。 使用向量化线性回归对比使用for循环完成的线性回归,更简洁。
1-1机器学习的相关名词
database mining 数据挖掘
machine learning
Grew out of work in AI:从人工智能发展出来的一个领域
New capability for computers :为计算开发的一项新功能
Examaples:
领域一:database mining 数据挖掘
例子:web click data 网络点击数据 ,medical records 医疗记录 ,biology生物学-基因序列,engineering 工程学所有领域
领域二:Applications can‘t program by hand 无法手动编写的程序
例子:Autonomous helicopter 自动直升机飞行 (让计算机自己学习飞行),handwriting recognition 手写识别 ,Natural Language Processing(NLP)自然语言处理 和 Computer vision 计算机视觉 理解语言与图形的领域
领域三:self-customizing programs 私人定制程序
例子: Amazon ,Nexflix product recommendations 亚马逊和。。的商品推荐功能 (学习算法)不会为每个人定制一个程序,而是让机器自我学习,最后为客户量身定制推送
领域四:Understanding human learning 研究人脑的学习。
1-2 什么是机器学习?
1.definition 定义
并没有统一的定义,下面是一些大佬们的定义。
①1959 Arthur Samuel在没有明确设置程序的情况下,使计算机具有学习能力的领域. 讲了一个samue的跳棋案例 与机器对弈,学习输赢的布局 分析更易胜利的布局,机器比人更有耐心。
② 1998 Tom Mit'chell(好友) 计算机程序从经验E中学习, 解决某一任务T 并进行某一性能度量P,通过P测定在T上的表现是否因经验E而提高。
经验E:程序与自己下几万次跳棋
任务T:玩跳棋
性能度量P:与新对手玩跳棋赢得概率
解释:计算机程序与人下棋博弈积累经验(E),目的是解决可以完成下棋任务(T)并取胜,评测与新对手下棋时获胜的概率(P)是否会因下棋次数的积累而提高获胜概率。
总结:有三个基本的要素,任务T、经验E和性能P。机器学习=通过积累经验E并进行改进后,机器在任务T上的性能度量p的性能有所提高=T–>(从E中学习)–>P(提高)
2.课间问题:
Suppose(假设) your email program watches which email you do or do not mark as spam(垃圾邮件),and base on that learns how to better filter(过滤) spam ,what is the task T in this setting (例子)?
A.自动分类邮件为垃圾邮件或不是垃圾邮件(T)目的:利用程序判断是否为垃圾邮件
B.观察你是否将邮件标记为垃圾邮件(E)自动学习并积累经验
C.正确归类邮件的比例(P)性能度量判断模型的准确率
2.主要的机器学习算法的分类
①supervised learning监督学习:我们教会计算机做某些事
②unsupervised learning 无监督学习:我们让计算机自己学习 (最常用的两种)
③其他算法:Reinforcement learning 强化学习 ,recommender systems 推荐系统
建议:知道如何高效的使用这些算法。
1-3有监督学习及常用算法
补充:监督学习与无监督学习【机器学习笔记】有监督学习和无监督学习_Liaojiajia-Blog-CSDN博客_有监督学习
1.定义
数据是提前做好分类的,都是适用于模型的数据,训练的样本同时包含特征和标签信息(目的)的,通过这些已有的训练样本去训练得到一个最优模型,对输出对实际值对比分析,实现预测或分类的目的,再利用这个模型去预测位置数据。 简单来说,就是有很多道练习题,每道练习题都给出了正确的答案,通过建立模型,将这些题目进行导入反复训练(训练集),然后用一部分题目检验这个模型的准确度(检验集),最后用一个准确率较高的模型来预测未知的题目。
有监督算法常见的有:线性回归算法、BP神经网络算法、决策树、支持向量机、KNN(最邻近节点算法),利用这些算法来解决实际应用问题。
2.两种数据类型补充:categorical data离散(分类型)数据与numerical data连续(数值型)数据
categorical[ˌkætəˈɡɔːrɪkl] data :是指某一特征下的值的个数是可数的,比如性别0或1,而且一般情况下不同value之间的距离是无法衡量的,比如颜色{红,黄,蓝}, 可以用0.1.2(中间有无数小数)来进行表示。细分部分可以归纳到一类。
⭐补:Categorical特征常被称为离散特征、分类特征,数据类型通常是object(对象)类型(https://baijiahao.baidu.com/s?id=1618844359785256101&wfr=spider&for=pc详解),而我们的机器学习模型通常只能处理数值数据,所以需要对Categorical数据转换成Numeric特征,Categorical又有两类,一种是定序型变量(ordinal:序数,顺序的)如下面的成绩分为ABCD四个object类型数据,直接导入模型是不可以的,需要转化成数值型数据才可以(数据处理那一块),一种是定类型变量,血型之间没有大小之分,A\B\O\AB,可以归为一类,同样可以用数值型数据1234转换。
个人感觉两个都属于分类数据,一个是可排序型分类数据,一个是不可排序型分类数据。
numerical[nuːˈmerɪkl] data :是指能无限细分的叫做连续型,比如长度,重量,温度等等 细分会对结果有影响,准确性。
3.有监督学习与回归问题、分类问题的关系
有监督学习 包含两种常见的监督学习问题:分类问题与回归问题,包含关系。
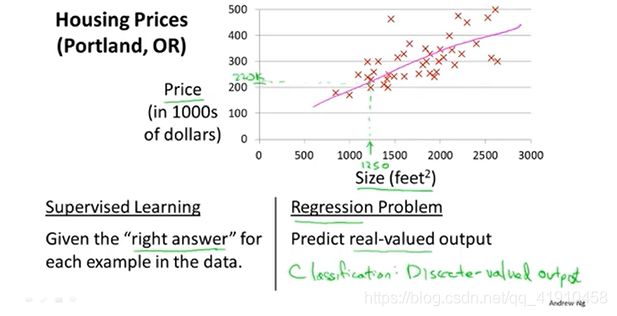
1.判定:给算法一个数据集,每一个样本数据明确的告诉了正确答案(一个房源数据集,每一个房子都给出正确的价格)算法的目的就是给出更多的正确答案(T)房子估价或者是肿瘤的良性问题
2.举例:
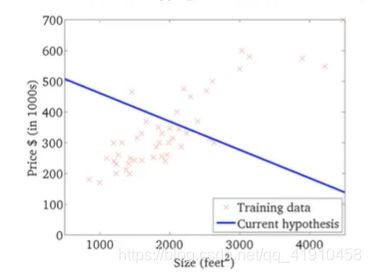
这是一个监督学习算法的例子,因为每一个样本数据明确的告诉了正确答案,某一房源的大小、房价,而且也是一个回归问题,回归是指我们预测一个具体的数值输出,某一肿块的判断是良性还是恶性
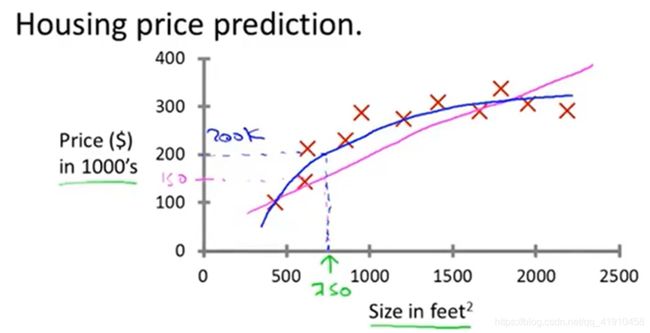
①常见监督学习之回归问题——房价预测案例:因为价格是连续的,而非离散的,用离散来做会影响准确性。后期选择是用直线拟合数据还是用二次函数拟合数据,无论哪个模型都不会影响房子的实际卖价,影响的是预测价格。
横轴:房间面积
众轴:价格(单因素)
回归问题(设法预测具有连续值的特征属性,可以看作回归问题):Predict continiuous (这个案例的回归问题是预测连续的数值输出price,价格实际上是一个离散值(不带小数的那种),但通常是一个标量或者连续值)
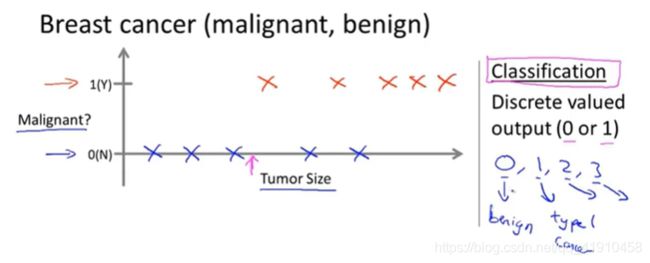
②常见监督学习之分类问题——乳腺癌检测案例
Classification(设法预测一个离散值的输出,0123.....可以是两个、也可以是多个类型):
众轴:是否为恶性肿瘤(可以是多分类)
横轴:肿块的大小(单因素,也可以是多个特征、属性)
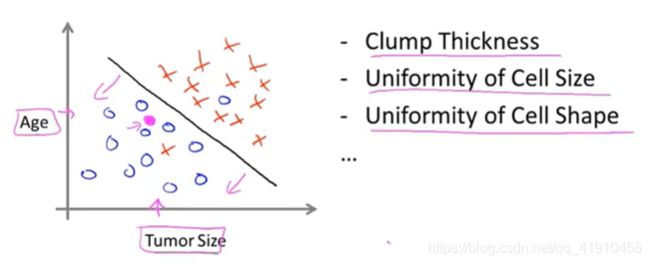
单个特征(肿瘤的大小)预测 (肿瘤的好坏) 多个特征(age、size)来预测 {svm支持向量机(可以处理无穷多个属性)}
课堂问题:学会对回归与分类的判断
你经营了一家公司,并且你想去通过算法来解决两个问题,判断是回归问题还是分类问题:
①你有很多identical(相同的)货物的inventory库存,你想预测接下来的三个月你能卖多少件(回归)因为将卖出的数量看作一个连续的值,
②你有许多的客户,你想写一个软件(software)来检查每一个客户的账户,判断这个账户是否被入侵或者破坏 (分类)离散值0/1
1-4无监督学习
1.无监督学习:只给了一个数据集,没有给正确的答案 。让算法自己学习~找到其中的结构,并进行分簇
1.定义
训练样本的标记信息未知, 目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础,此类学习任务中研究最多、应用最广的是"聚类" (clustering),聚类目的在于把相似的东西聚在一起,主要通过计算样本间和群体间距离得到。深度学习和PCA(主成分分析技术)都属于无监督学习的范畴。
算法:clustering algorithms聚类算法 (其中主要的一种)
案例①Goole news: 每天收集上万个新闻,自动的分簇、然后将他们组成到一个个新闻专题中,同一族的就会被显示到一起。
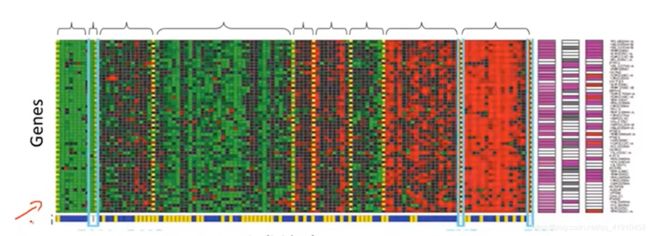
②基因组序列检测:给定一组不同的个体,对于每个个体,检测他们是否拥有某个特定的基因(特定基因的表达程度),红绿黄表达了拥有某些特定基因的程度,然后运用聚类算法把不同的个体归入不同的类或者不同类型的人。(只是告诉算法这有一堆数据,我不知道这些数据是什么、不知道谁是什么类型、也不知道有哪些类型,让算法自动找出这些数据的结构,让算法自动的按照得到的类型将这这些个体分成簇)
2.无监督学习之聚类算法的现实应用
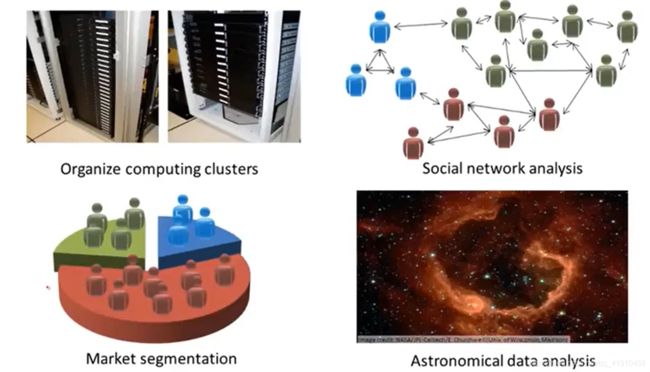
| Organize computer clusters 组织大型计算机集群 | 找到哪些机器趋向于协同工作,将这些数据放在一起就可以让计算机更让高效的工作 |
| social network analysis社交网络的分析 | 若知道emile最频繁联系的人、或者微信好友、一些圈子的好友,可以自动判别同属于一个圈子的好友、判断哪些人互相认识 |
| Market segmentation市场细分 | 公司拥有大量的客户数据库,根据客户数据集可以自动找出不同的市场分割,并自动将客户分到不同的细分市场,从而可以精确的在不同的细分市场销售(我们只有客户数据,并不知道有哪些细分市场,也无法知道谁属于细分市场之一,让算法自己去发现) |
| Astronomical data analysis 天文数据分析 | |
ng推荐语言:Octive,来建立学习算法原型,然后迁移到其他语言编译环境, 会更有效率,现在主流的语言还是python。
---------------------------------------------------------------------------------- 进入正题 -------------------------------------------------------------------------------------------------
2-1第一个学习算法—线性回归算法
1. 课程中符号的表示:
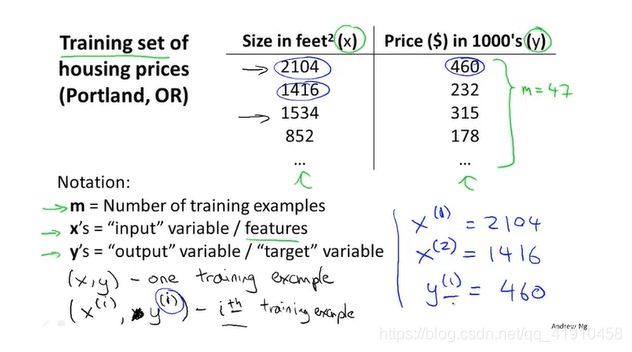
监督学习里有一个数据集,也叫训练集,从这个训练集中进行学习做一件事情。
m:训练样本的数量
x:输入变量(特征)
y:输出变量( 要预测的目标特征)
(x,y):一个训练样本
![]() :表示某一个样本,第i个训练样本
:表示某一个样本,第i个训练样本
![]() :假设函数
:假设函数
θ0、θ1:模型参数
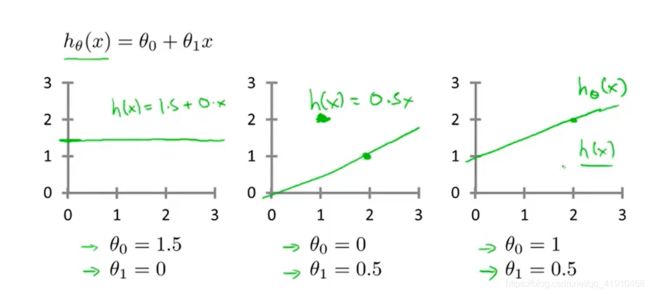
2.监督学习算法的工作过程以及线性回归模型的介绍(单变量)
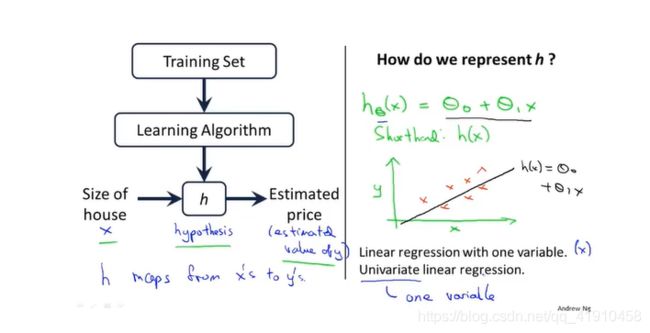
1.学习算法的工作过程:将训练集数据导入一个学习算法,输出(确定)一个函数h(假设函数)hypothesis,作用是将房子的大小作为输入变量x,它会对应输出房子的预测值y, 假设函数 h是引导从x得到y的一个函数。
2.学习算法的设计:当我们设计一个学习算法时,要知道怎么表示这个假设函数h。如![]() 表示的是下面的一个预测y关于x的线性函数(学习基础)然去学非线性函数,这个模型也叫线性回归模型(一元线性回归)中的单变量线性回归。
表示的是下面的一个预测y关于x的线性函数(学习基础)然去学非线性函数,这个模型也叫线性回归模型(一元线性回归)中的单变量线性回归。
下面介绍如何动手实现这个模型
2-2代价函数|平方误差函数|平方误差代价函数(取决于误差项的平方和)
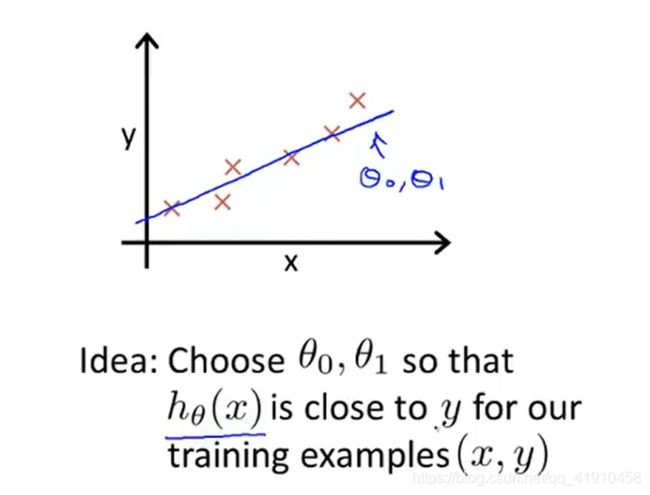
1.代价函数的作用:不同的参数,假设函数模型也不同。弄清楚确定最有可能的直线与我们的数据相拟合(优化目标)调试参数得到最有可能的直线与我们的数据相拟合 ,确定最优的模型参数θ0、θ1的值,减少预测值与真实值之间的误差·。
2.举例说明代价函数的功能
x:表示卖出的哪个房子
y:表示房子的实际价格
hθ(x):预测值,输入x时我们预测的房价值,最接近该样本对应的y值时得参数θ0、θ1
目的:在训练集中给出训练集中的x值,我们可以合理的预测y的值
3.总结:在线性回归中我们要解决的是一个最小化的问题(minnimization) (为什么要这两个参数最小?因为代价函数j(θ0,θ1)最小时模型参数最小,假设函数h(x)也是最小的,预测值与真实值的差异最小)
(为什么要这两个参数最小?因为代价函数j(θ0,θ1)最小时模型参数最小,假设函数h(x)也是最小的,预测值与真实值的差异最小)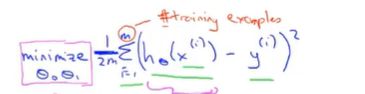 。
。
4.选择平方误差作为代价函数目的:h(x)和y之间的差异要小,预测值更无线接近真实值。要做的一件事是最小化假设输出与房子真实价格之间的平方差,因为平方差更能反应真实的误差。有m条数据,所以要对每一条样本误差累计求和取平均误差的最小值时候的参数。平方误差代价函数是解决(线性)回归问题最常用的手段。
涉及知识:最小二乘法
4.代价函数(Cost Function)的数学定义:用于衡量一个假设函数的损失(预测值与真实值之间的误差),损失越小说明假设函数越适用,也叫平方和误差函数。
核心公式如下: 2分之1就是为了(后面求导)好计算一些,因为常数对求导不造成影响,结果值都是一样的,而且主要是在一组参数中选一个代价函数最小的,大家同除2,对结果没有影响,最小的参数还是最小。
⭐解释:求样本的每一条数据的假设值与真实值之差的平方求和,除以两倍的样本数量。若总体的真实值与总体的假设值差别巨大,会造成代价函数 ![]() 的值较大(因为输入值都是固定的,变的是θ0,θ1两个参数),所以我们的目标为,求使得
的值较大(因为输入值都是固定的,变的是θ0,θ1两个参数),所以我们的目标为,求使得 ![]() 取最小值(总体真实值与假设值差别最小)时候的
取最小值(总体真实值与假设值差别最小)时候的 ![]() 和
和 ![]() ,而不是让假设函数最小时的,总体代价函数小,假设函数输出值与真实值的误差也小,假设函数最小的参数,整体不一定最小。因为
,而不是让假设函数最小时的,总体代价函数小,假设函数输出值与真实值的误差也小,假设函数最小的参数,整体不一定最小。因为![]() ,在x固定的情况下,参数越小假设函数越小,但是代价函数不一定是小的,因为(是平方差,h(x)小与y之间的平方项反之变大了)
,在x固定的情况下,参数越小假设函数越小,但是代价函数不一定是小的,因为(是平方差,h(x)小与y之间的平方项反之变大了)
参考:吴恩达机器学习(一)单变量线性回归(假设函数、代价函数、梯度下降)_今天你学习了吗-CSDN博客
下一课详细学习代价函数的原理、计算目的、使用目的、为何使用
2-3代价函数
(一)简单了解代价函数原理
1.简化的代价函数
为了更好的使得代价函数可视化,更好的理解代价函数的概念,我们使用一个简化的假设函数,使它仅包含参数![]() ,令
,令![]() 如右图所示。假设函数就变为
如右图所示。假设函数就变为![]() (是关于x的函数),优化目标就是尽量减少
(是关于x的函数),优化目标就是尽量减少![]() (是关于
(是关于![]() 的函数,控制直线的斜率)的值。图形表示为经过原点的假设函数。
的函数,控制直线的斜率)的值。图形表示为经过原点的假设函数。
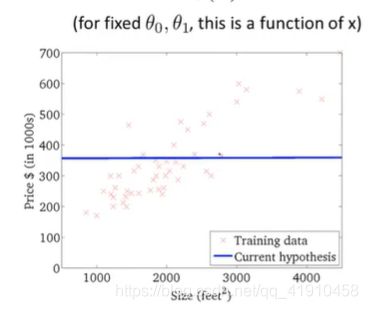
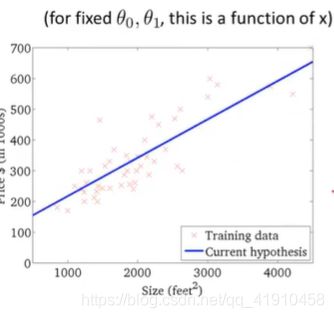
2.绘制假设函数与代价函数关于各自变量的图形
简化算法: 假设![]() 参数为0(可以是负数),简单推导 为何选择参数最小时的代价函数。
参数为0(可以是负数),简单推导 为何选择参数最小时的代价函数。
训练集中有三个数据:(x(输入的特征值),y(真实值)):(1,1),(2,2),(3,3)
目的:找一条拟合度最优的线,通过改变![]() 的值,得到不同的代价函数值,然后找到最小值时的参数。
的值,得到不同的代价函数值,然后找到最小值时的参数。
过程:要弄清当参数θ变化时,代价函数的变化
①假设![]() 等于1时------->斜率为1的直线,因为选的点都是特殊点,当等于1时候
等于1时------->斜率为1的直线,因为选的点都是特殊点,当等于1时候![]() 正好经过这些点,那么此时的代价函数的值为0
正好经过这些点,那么此时的代价函数的值为0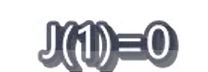 。观察预测值(假设函数h(x)的值)与真实值的拟合度然后求代价函数的值,描绘代价函数依据参数
。观察预测值(假设函数h(x)的值)与真实值的拟合度然后求代价函数的值,描绘代价函数依据参数![]() 变化的图形,如右图所示。
变化的图形,如右图所示。
②假设![]() 等于0.5------->斜率为0.5的直线,
等于0.5------->斜率为0.5的直线,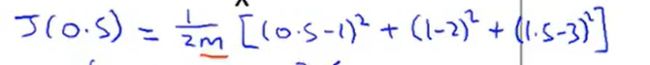
 = 0.58
= 0.58
④同理当参数为负数时候
。。。。。
⑤画出最后大致图像如下:分析的出在令![]() 值最小时候的参数
值最小时候的参数![]() ,与真实值的拟合程度是最高的。
,与真实值的拟合程度是最高的。
3.总结:学习算法的优化目标是我们选择参数![]() 的值获得最小的
的值获得最小的![]() ,通过观察
,通过观察![]() =1的时候代价函数最小,并且此时的假设函数是一条符合数据的直线,以上就是为什么要最小化代价函数。找到最能拟合数据的线。
=1的时候代价函数最小,并且此时的假设函数是一条符合数据的直线,以上就是为什么要最小化代价函数。找到最能拟合数据的线。
回归原来公式,观察同时包含两个参数时候的图形。
2-4代价函数
(二)深入理解
1.与前一节不同点:保留全部参数,有两个参数
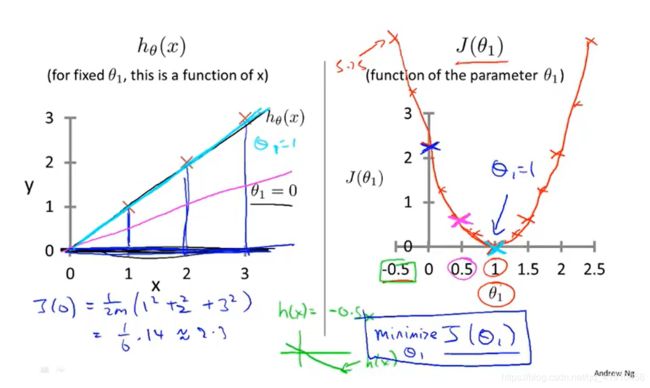
2.代价函数3D图形
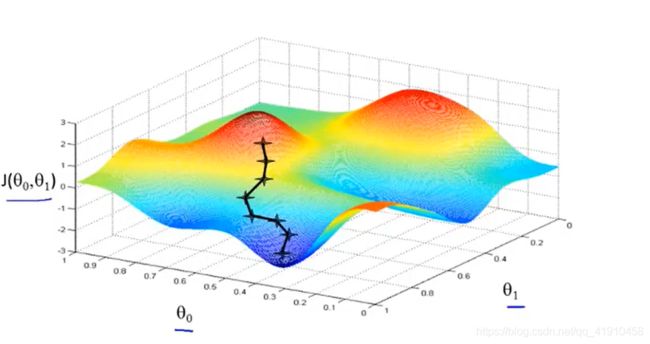
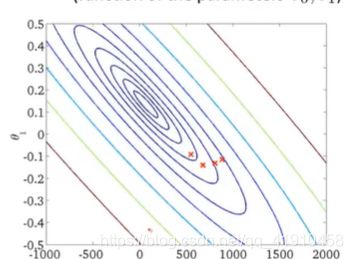
代价函数的3D曲面图形(碗状),横轴为两个参数![]() ,代价函数的值随着这两个参数的变化而变化,曲面的高度也就是代价函数的值。
,代价函数的值随着这两个参数的变化而变化,曲面的高度也就是代价函数的值。
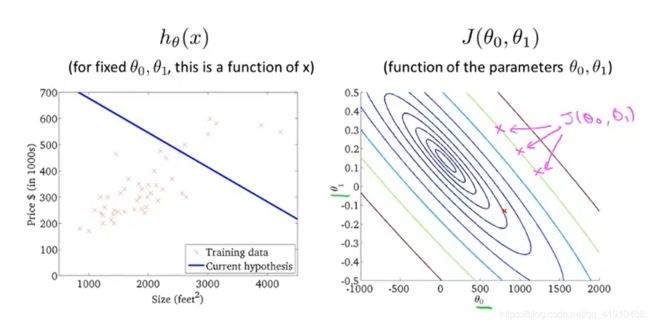
3.代价函数二维图形
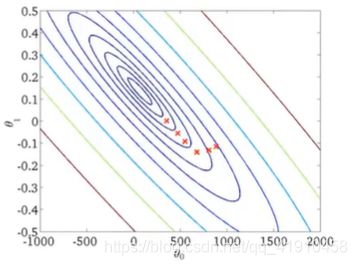
为了更好的展现图形,同一高度的点、转化为2D图形,使用等高线图(contour plots) , 轴为两个参数![]() , 每一个椭圆形表示
, 每一个椭圆形表示![]() 相等的点,每个都对应着一个假设函数
相等的点,每个都对应着一个假设函数
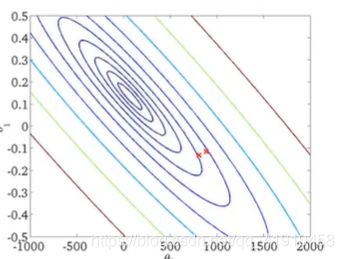
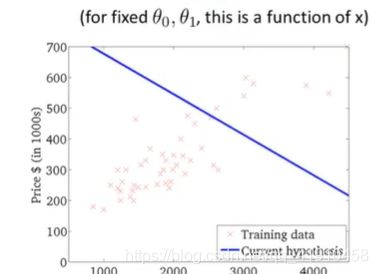
①如下图1点所对应的两个参数描绘的h(x)直线图形,并没有很好的拟合数据,因为代价值距离最小值还有很大的距离 ,因为拟合的不好,只有代价值最小时候,才是拟合最好的假设函数h(x)。
,因为拟合的不好,只有代价值最小时候,才是拟合最好的假设函数h(x)。
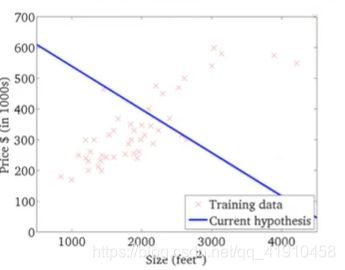
②如图2点所示:虽然不是最小值点,但是相当接近最小值,表明函数对数据拟合的还不错,但是还是存在着一定的平方误差。
4.总结:代价函数最小值的点对应着更好的假设函数。
学习目的:想要一个高效的算法或软件、来自动的寻找代价函数J的最小值, 以及对应的两个参数的值。而不是找一个绘图软件,手动读取参数。
后期还会遇到一些多参数的、更高维的,可视化图形很难描绘的,我们需要利用软件来自动寻找使代价函数最小的参数的算法
下一课内容:找到一种自动找到使函数J参数最小的算法。
2-5 梯度下降 Gradient descent (同步更新参数)
1.功能:应用于机器学习的各个领域,可将代价函数J最小化的梯度下降法,不仅可以最小化代价函数,也可以最小化其他函数。
2.应用:优化线性回归中的代价函数
3.问题概述:我们有一个函数![]() ,也许是一个线性回归的代价函数,也许是一个需要最小化的其他函数,我们需要一个算法来最小化函数
,也许是一个线性回归的代价函数,也许是一个需要最小化的其他函数,我们需要一个算法来最小化函数![]() ,也可以最小化其他函数。为了简化符号下面的视频只用两个参数。
,也可以最小化其他函数。为了简化符号下面的视频只用两个参数。
4.梯度下降的思路outline:⭐
①开始给定θ0,θ1一个初始值,是什么并不重要,通常两者初始值都设置为0。
②接下来不停的一点点的改变θ0,θ1的值来使代价函数变小,直到找到最小值或者局部最小值
5.图形展现梯度下降法的工作过程:
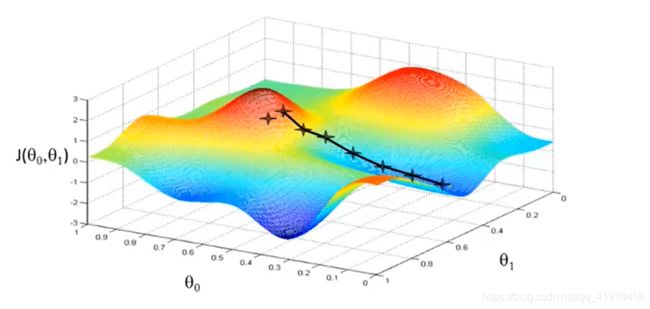
如图1 ,我们想最小化这个函数,我们从θ0,θ1的某个值出发=从这个函数图形的某个点(参数为0点,也可以是其他点)出发 。是看作成两个小山,想尽快下山(到最低点)应该朝着哪个方向迈步(下降最快)? 站在这一点,环顾四周找到一个最合适的下山方向迈步,到带你一个新的起点,然后重复该过程,直到收敛至局部最低点。
一个有趣的特点:当存在多个局部最优值时候,第一次选用不同的点开始梯度下降时,可能会找到另一个局部最优处。
问题:什么时候达到局部最优停止参数更新???
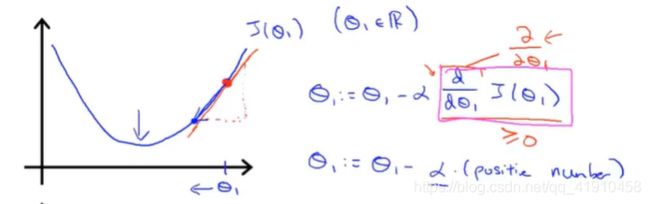
6.梯度下降算法的数学原理(定义):重复做这一过程,直到收敛 同步更新θ0,θ1
①符号介绍:
θj:模型参数
:=: 赋值符号,a:=b表示将b的值赋值给a a=b这里指的判断
α:学习率,用于控制梯度下降速度,迈出的步子(下降的速度,大小如何设置后期会讲)(更新参数的幅度)
②数学定义
⭐7.公式解释:
①过程同时更新θ0与θ1,![]() 会更新θ0与θ1的值,
会更新θ0与θ1的值, ,
, (两者同时进行),将更新后的参数值进一步带入更新,如图一。
(两者同时进行),将更新后的参数值进一步带入更新,如图一。
②必须是同步更新,一个参数的变动,若不同时更新,计算另一个参数时候,是用更新过的θ值,而不是最初的值。 如图2,参数θ0更新后直接利用新的参数θ0去更新参数θ1,而非初始值θ0去计算导数项,是错误的,因为后面的代价函数是关于两个参数的方程式。
③为什么梯度下降要同步更新:同步更新是更自然的实现方法,谈到梯度下降就是同步更新,如果使用非同步跟新去实现算法,可能也会正确工作,但不是人们所指的那个梯度下降法,而是具有不同性值的其他算法。
下一课讲解:导数项 相关基础:微积分课程:偏导数与导数。 进一步了解如何使用梯度下降法
。
2-6 梯度下降知识点总结
1.学习内容:了解梯度下降算法的用途,更新过程的意义:这两部分的作用,为何将学习率与导数项放在一起整个更新过程才是有意义的。
2.梯度下降法的更新规则:不断根据公式更新参数的直到最小值(参数值最小处)(从函数的某个参数值点出发,开始梯度下降),可以从左边开始,也可以从右边。
3.举例说明,导数项的意义
最小化函数只有一个参数的代价函数,试着理解梯度下降法在这个函数上起什么作用。
①初始化参数选取在右边时:代价函数的一维曲线如下(并没有实际画出,只是大致轮廓,它在自动寻找最优参数):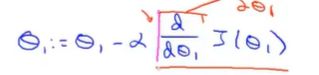 其中导数项其实是代价函数的斜率。 如图有一个正斜率,也就是正导数,因此得到的新的参数,
其中导数项其实是代价函数的斜率。 如图有一个正斜率,也就是正导数,因此得到的新的参数,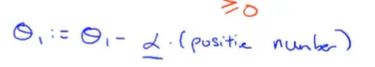 ,学习率永远是正数,因此参数会变小,向左移动更接近那边的最低点。
,学习率永远是正数,因此参数会变小,向左移动更接近那边的最低点。
②初始化参数选取在左边时:导数项是负斜率,然后更新参数![]() ,实际上参数大小增加了,向右移动
,实际上参数大小增加了,向右移动
4.学习率 α
α的大小会有什么影响:
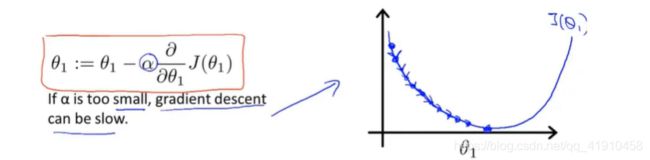
①学习率太小时:梯度下降的速度会变得很慢,一小步一小步的更新去接近最低点。
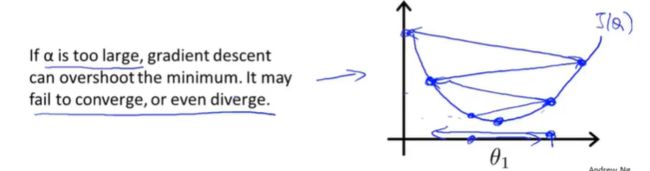
②学习率太大时:会出现过拟合现象,每次更新一大步,导致梯度下降可能会越过了最低点,无法收敛(好像是导数趋于0)甚至发散。 如下图所示:
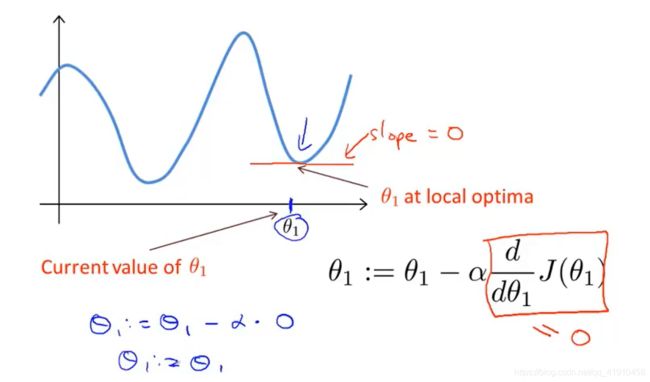
③狡猾的问题:若初始的参数值设置在了局部最优点(导数为0),下一步的梯度下降会如何?
那么参数值将不会再改变。导数项始终为0,会使你的解始终保持在局部最优点。
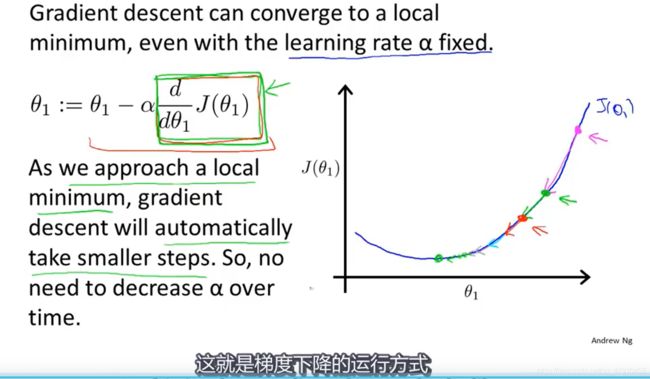
因此:即时学习速率保持不变,梯度下降法也会收敛到局部最低点的原因(导数项会逐渐变小,直到0达到局部最优点),再接近最优点时候,梯度下降法会自动采取更小的幅度。所以没必要另外再减少学习率,也不要太大。
⭐举例说明:首先初始化梯度下降参数,粉红点->绿色点,你会发现绿色点的斜率并没有粉红点处的斜率那么大,因为随着接近最低的点导数越来越接近0,然后再梯度下降一步到达红色点,更接近最低点了,此时的导数比在绿点更小。同时参数更新的幅度也会更小,随着下降移动的幅度会自动的变的越来越小,直到移动幅度非常小,此时已经收敛到局部最小值。
总结:梯度下降算法可以推广到最小化任何代价函数j
next:线性回归中的代价函数结合梯度下降算法,得到第一个机器学习算法:线性回归算法
2-7线性回归的梯度下降(迭代算法)
1.内容:梯度下降和代价函数的结合得到线性回归算法
2.目的:将线性回归得梯度下降算法用到最小平方差函数之中。①
3.导数项内容:求j等于0与j等于1时得偏导数-也就是分别求θ0与θ1得偏导数 这里需要补一补微积分求偏导得过程!自己推一推
4.导数项求导过程:这里很清楚得可以看出:多除个2,是为了求导后可以约分
求积对θ0求导其余项看作常数,求导时结合了复合函数求导
原理 :一个一元复合函数求偏导(其余元素看作常数)
①对θ0求偏导:对外层平方求导后得2与2m得2抵消,里面对参数求导为1
②对θ2求偏导:对外层求导后得2与2m得2抵消,在对内层的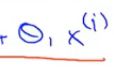 求导后得到个
求导后得到个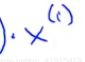
求出斜率(导数)之后,再带回梯度下降算法 不断更新迭代、直到代价函数达到最小 ③
④这里是线性回归的梯度下降法,也叫Batch(批量)梯度下降,。每一步梯度下降都遍历了整个训练集的样本,计算偏导数的时候,我们计算m个训练样本的总和,注意参数要同步更新,不断重复该过程直到收敛。还有其他的梯度下降,没有全拦整个训练集,每次只关注了小子集,后面会讲。
避免陷入局部最优(代价函数有多个最优解)‘
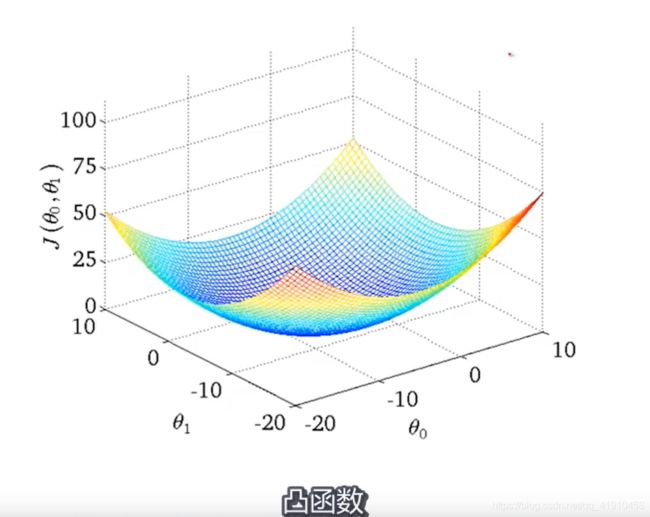
5.线性回归的代价函数图像:总是这样的弓状函数,也叫凸函数,没有局部最优,只有一个全局最优解。只要使用线性回归运用这种代价函数做梯度下降,总会收敛到全局最优。
6.算法的使用过程:
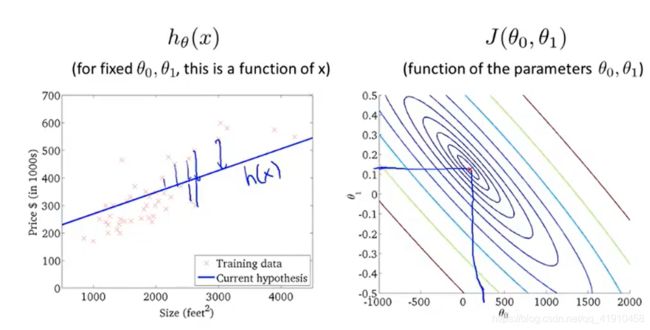
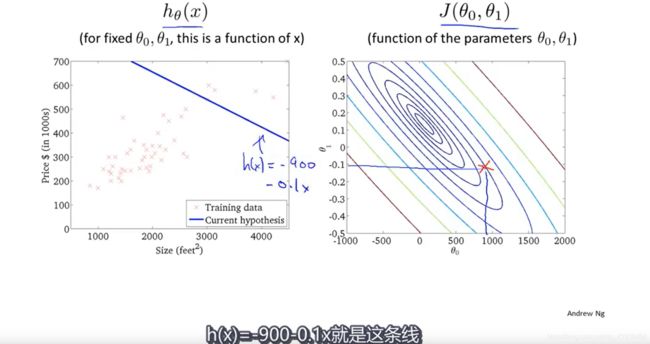
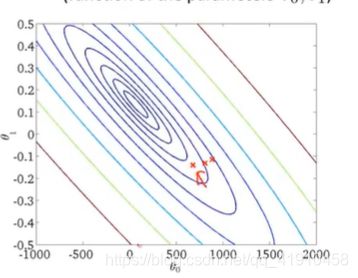
假设函数与代价函数如下,观察值的参数初始化,通常在0,0处初始化参数,更形象的解释梯度下降初始选为0_900,1_-0.1。假设函数会随着代价函数沿着最小值的轨迹变化,随着梯度逐渐下降,直到达到全局最小值。这时全局最小值对应得假设曲线很好得对应了拟合数据,利用拟合好的假设曲线就可以进行预测了。 过程如下:
7.总结:以上就是学习的第一个算法: 使用梯度下降的线性回归
补充:梯度下降适用于大数据集,并且在不同机器学习上都可以用。线代中得正规方程组方法也可以快速求最小值,不需要多次迭代。
next:介绍梯度下降的通用算法
3.矩阵与向量知识
1.矩阵和向量(Matrices and vectors)
内容:介绍矩阵与向量的概念
1.矩阵的定义:由数字组成的矩形阵列,写在方括号内,也可以说是二维数组的另一种说法。矩阵的维数就是矩阵的行数*列数。矩阵可以让你快速整理索引和访问大量数据。
2.矩阵的项(元素):矩阵的中的某一个元素,用行与列表示,常用大写字母表示。如下图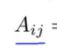
3.向量的定义:一个向量是一种只有一列的特殊的矩阵。
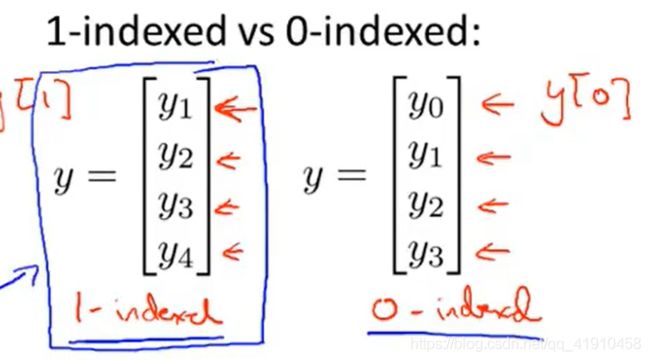
4.向量的下标表示:有时候会从1开始表示(矩阵、大部分数学表达中),一些编程语言种的数组是从1开始排序的,有些机器学习问题0下标向量为我们提供了一个更方便的符号表达。除非特别指定,默认使用1下标开始。一般用小写字母表示向量。
2.加法与标量乘法
学习内容:矩阵的加法与减法运算、乘法运算(标量乘法)
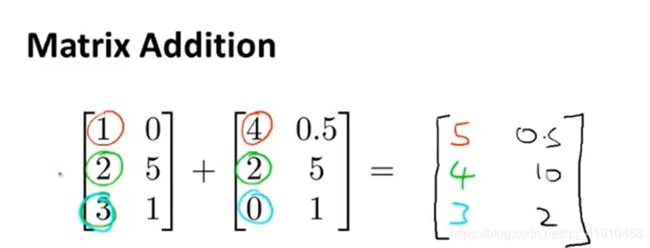
1.加(减)法运算:同纬度矩阵,对应相加(减)。
2.矩阵与标量(实数)的乘(除)法运算: 逐一相乘。
3.矩阵向量乘法
1.目的:可以简化代码,通过计算机矩阵相乘的方式就可以算出计算值,比写for循环一个函数更简单
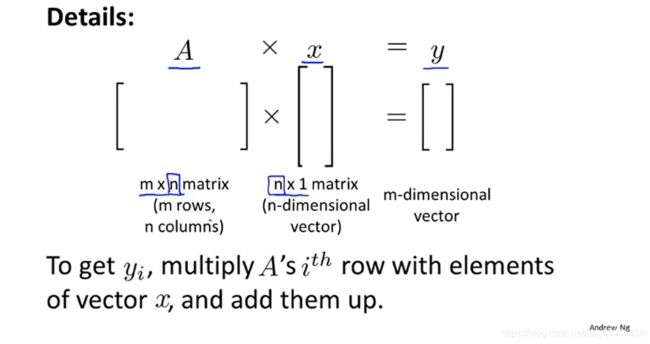
2.特列:矩阵与一个向量相乘,对应(行列)相乘再相加,M*NxN*K=M*K
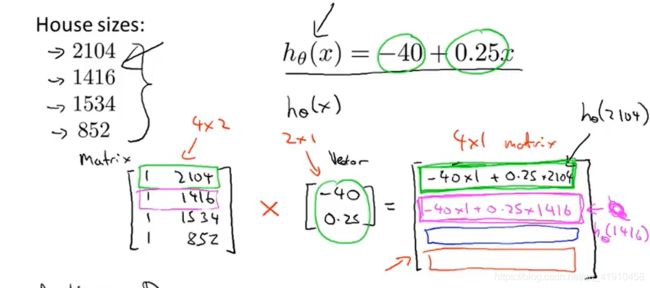
3.实际应用:假设有四间房子,有四种大小,有一个假设函数可以预测房子的价格,可以利用矩阵相乘来预测房子的价格。利用矩阵就可以只写一行代码就完成整个过程。 。特征矩阵与参数矩阵的相乘。当有1千个房子需要预测时,写一个for循环即可
。特征矩阵与参数矩阵的相乘。当有1千个房子需要预测时,写一个for循环即可
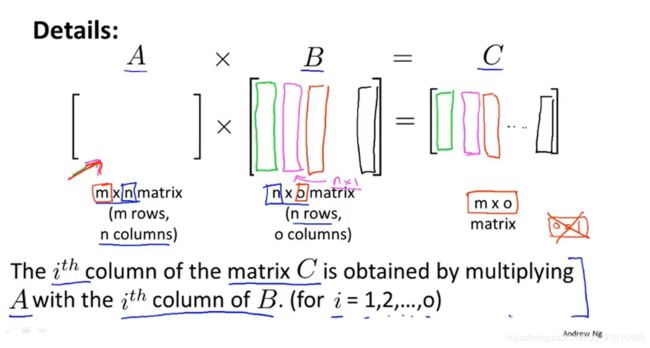
4.矩阵乘法
1.目的:将两个矩阵相乘,在线性回归中,用于同时解决参数θ0与θ1的计算问题,而不需要梯度下降法这种迭代算法。矩阵与矩阵的运算是必须理解的关键步骤。
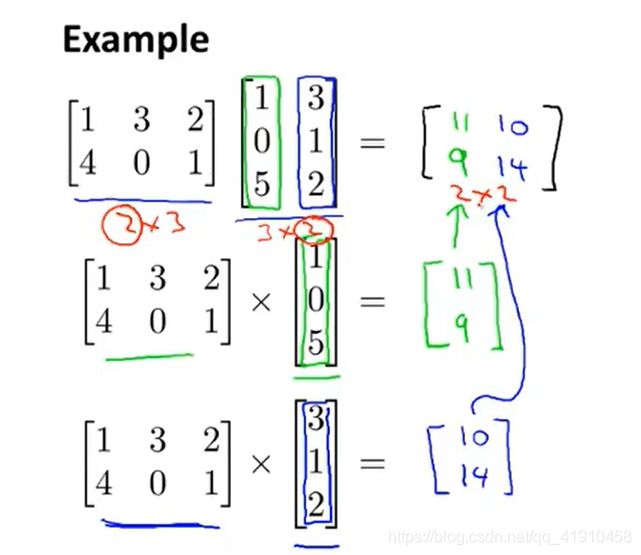
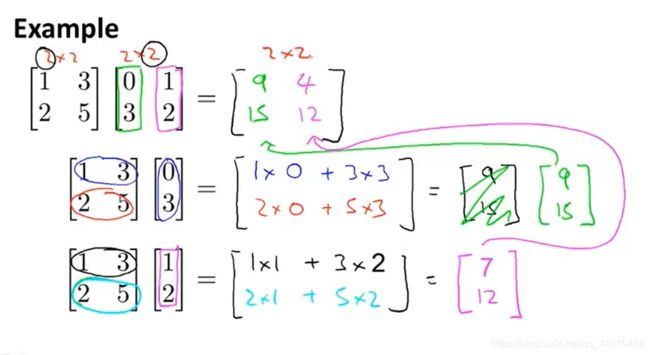
2.举例:矩阵相乘的原理。拆接成矩阵与向量预算,再拼接
3.计算矩阵C过程:要获得矩阵c的第i列,要用矩阵A和(矩阵B的第i(for i =1,2,3,,,o )列)相乘得到,竖着写!再拼接
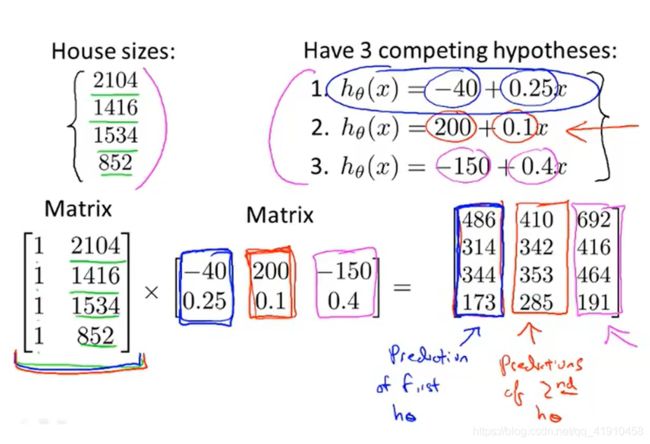
4.矩阵与矩阵乘法简洁技巧:实际应用,假设预测四间房子的价格,有四个预测特征值、3个假设函数(看哪个更精确),想将这三个假设函数都用于这4个房屋,使用矩阵乘法,一次运算可以得到多种假设函数的预测值。矩阵构造如下:结果每一列就是对应假设函数的预测结果。
引用1向量与常数参数相乘。
5.总结:现在的编程语言基本上都带有优秀的线性代数库,来进行高效的矩阵间的乘法运算,可以快速的基于众多假设进行预测。
5.矩阵乘法的特征
1.用处:可以打包大量的运算,然后用一次矩阵的乘法运算。
2.特性
①标量乘法可交换性
②矩阵乘法不满足交换律:
③矩阵乘法满足结合律:
④单位矩阵满足交换律
6.矩阵的逆运算与转置(与实数运算区别)
1.逆矩阵的定义:前提是方阵,只有方阵才有逆矩阵一个矩阵A与其矩阵B相乘得到一个单位矩阵C,则矩阵B就是A的逆矩阵。
2.求逆矩阵的方法:①根据所学知识手算 ②利用软件链接开源库即可或任何主流语言 求解逆矩阵 这里用到的是Octive
3.什么样的矩阵没有逆矩阵:不是方阵的矩阵,矩阵元素全为0,注意:行列式不为0才有逆矩阵 不存在逆矩阵的矩阵——奇异矩阵或退化矩阵,想成非常近似于0
next:构建线性回归、 多数据、多样本、多特征、、、、、、然后用学到的矩阵工具推导更多的算法
4-1多元线性回归
1.内容:讨论一种新的线性回归版本 ,这种形式适用于多个变量或多特征。
2.对比:
①之前版本,只有一个单一特征量房屋面积x来预测价格y,并有一个假设函数
②现在版本:不仅有房屋面积还有卧室数量、楼层数量、房子年龄等多特征用来预测价格的信息。
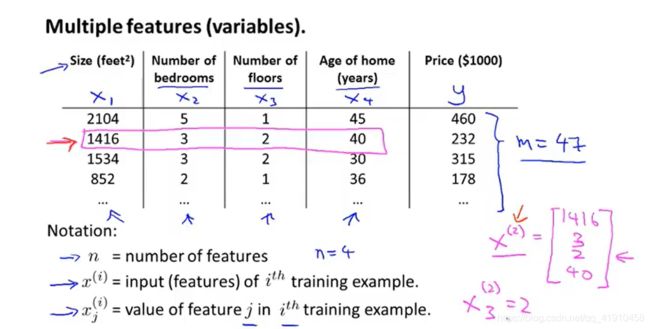
3.数据表示方式
n:特征值的数量,x1,x2,x3.。。
m:训练样本数
xi:表示特征值变量
y^i:表示第i个样本数据的真是值
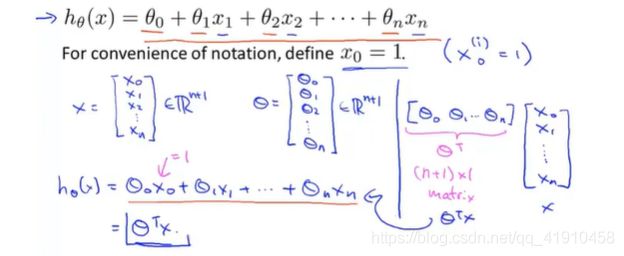
5.上面假设形式的简化:为了表示方便将x0的值设为1,具体而言,这意味着对于第i个样本,都有一个向量X^(i),并且X^(i)_o总等于1,相当于我们额外定义了一个第0个特征量。因此新的特征向量X是一个从0开始标记的n+1维的向量。假设函数可以用下面内积的形式来表示。也叫多元线性回归。多元的意思就是多特征来预测y,![]()
多特征向量下的假设函数:多元线回归Multivariate linear regression
多元假设函数是一个多元线性方程(组)可以写成向量的内积的形式(线代知识) 假设的函数就是线性的~ 解方程组便会一次性得到多个预测值(然后找最接近的那个所对应的参数值最小)。假设函数的矩阵表示
将参数部分与特征值部分看作线性向量:每一个特征值都对应一个参数(表示两者的相关性:正数表示正相关,负数表示负相关)
4-2多元梯度下降法
1.学习内容:如何设定该假设函数的参数、并介绍如何使用梯度下降法来处理多元线性回归。
2.回归变量记号
②参数的表示:看作一个n+1维的参数![]() 向量,
向量,
③代价函数: 依旧通过误差项的平方和来表示,但是又不把j看作这n+1个 数的函数,而是使用通用的方式把J 写成参数![]() 向量的函数,
向量的函数,
![]()
④梯度下降:
一个特征与多个特征时的比较:前面没啥变化就是表示方式变了,多个特征值时 ,对应的参数也就变多,也就多加了几次参数的更新。
4-3 多元梯度下降法演练——特征缩放
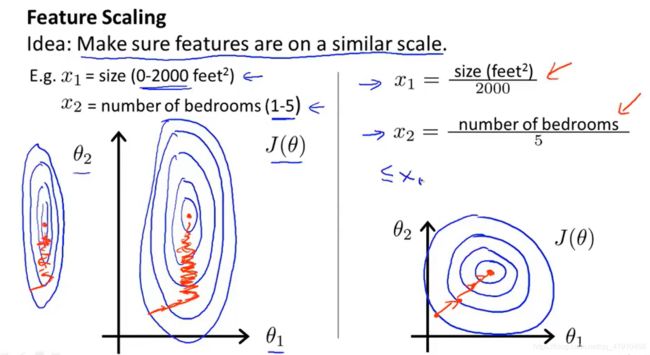
1.学习内容:梯度下降运算中的实用技巧——特征缩放的方法,到一个较小的范围,类似于归一化。
2.目的⭐:若有一个机器学习的问题,有多个特征,若能确保这些特征(不同的特征值之间)都处在一个相近的范围,那么梯度下降法就可以更快的收敛,更快的找到最小值。
由狭窄细长的椭圆——》圆
3.举例:有两个特征变量。X1为房屋的规格(0-2000),X2为卧室的数量(1-5) 确保不同的特征取值都在相近的范围内,梯度下降法就可以快速的收敛,若画出代价函数的等值线, 是一个关于参数
是一个关于参数 的函数,但是这里先忽略参数0,假设只有变量参数1,2,(这里是两个特征变量,若是三个及以上该怎么画?),那么代价函数的等值线就会出现非常歪斜并且椭圆的形状(特征值大) ,原因:代价函数原理就是假设函数,特征值是固定的,由于参数1的特征值比较大,当减小参数1时,θ1*x1+θ2*x2 ,参数θ2必须大幅度增加,才可以让两个式子等值。当两个特征值的取值接近的时候,两个参数可以类似反比例函数,有规律的变化,因此呈现均匀的椭圆形。此时等值线之间的距离比较均匀,到达最小值点的路程更短,运行梯度下降的速度更快。
的函数,但是这里先忽略参数0,假设只有变量参数1,2,(这里是两个特征变量,若是三个及以上该怎么画?),那么代价函数的等值线就会出现非常歪斜并且椭圆的形状(特征值大) ,原因:代价函数原理就是假设函数,特征值是固定的,由于参数1的特征值比较大,当减小参数1时,θ1*x1+θ2*x2 ,参数θ2必须大幅度增加,才可以让两个式子等值。当两个特征值的取值接近的时候,两个参数可以类似反比例函数,有规律的变化,因此呈现均匀的椭圆形。此时等值线之间的距离比较均匀,到达最小值点的路程更短,运行梯度下降的速度更快。
4.特征缩放:将特征的取值约束到-1——+1(或者其他范围, 不能太大或太小,和这个接近就可以)的范围内,因为特征值x0总是等于1,因此已经在这个范围内了。对于其他的数则要通过除与不同的数来让他们处于同一范围内。
特征放缩的方法①:除以特征值的最大值
②均值归一化(常用):无论哪种将特征值转化为相近似的范围即可,并不需要太精确,只是为了让梯度下降,运行的更快一些而已。收敛所需的迭代次数更少。
原理:xi用xi-ui来替换,让特征值具有为0的平均值。我们并不需要把这一步应用到x0中,因为它总是等于1,不可能有为0的平均值,对于其他特征而言,如房子的大小取值在0-2000,面积的平均值为1000,则可以用这个公式算出新的特征x1和x2,在某一范围中。
⭐更一般的规律:特征缩放 ,并不需要太精确,只是为了让梯度下降运行的更快些而已,收敛所需的迭代次数更少。
![]()
u_1是特征x_1的平均值、s_1是特征值的范围(max-min或者标准差)
next:介绍另一种方法来使梯度下降在实践中工作的更好。
4-4多元梯度下降法Ⅱ---学习率
1.学习内容:集中讨论学习率、调试技巧确保梯度下降正常、如何选择学习率。
2.如何确保梯度下降算法是否正常收敛
①方法一绘图(ng常用):
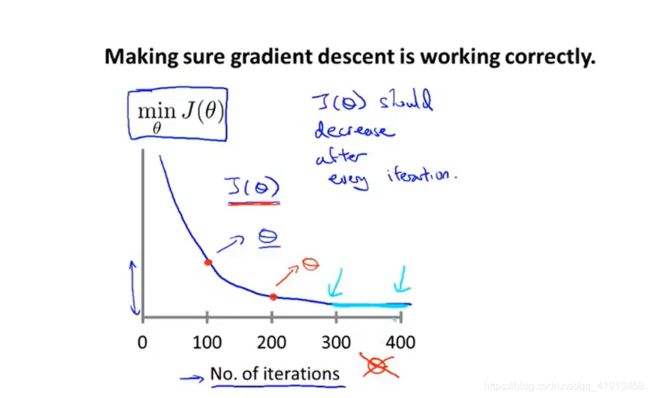
在梯度下降算法运行时,绘出代价函数![]() 的值,这里x轴表示梯度下降算法的迭代次数,(注意之前的x轴表示的是参数),y轴表示随着梯度下降算法迭代次数的运行得到参数θ算出的代价函数的值,这个图表示的梯度下降的每步迭代后 代价函数的值,如果梯度下降算法正常的话,每步迭代之后代价函数都会下降,直到收敛无法下降。通过这个图像可以判断是否梯度下降算法是否收敛,还可以判断算法是否正常工作。
的值,这里x轴表示梯度下降算法的迭代次数,(注意之前的x轴表示的是参数),y轴表示随着梯度下降算法迭代次数的运行得到参数θ算出的代价函数的值,这个图表示的梯度下降的每步迭代后 代价函数的值,如果梯度下降算法正常的话,每步迭代之后代价函数都会下降,直到收敛无法下降。通过这个图像可以判断是否梯度下降算法是否收敛,还可以判断算法是否正常工作。
梯度下降逐渐收敛 表示是正常的(参数逐渐缩小到最小值,未发生跳跃)对于不同的问题,迭代的次数也是不同的,实际上我们很难提前判断需要迭代多少次数。
②自动的收敛测试:利用算法来判断梯度下降算法是否已经收敛。若是代价函数迭代之后的值小于一个很小的阈值,这个测试就判断函数已经收敛,但是要选择一个合理的阈值是非常困难的,所以更倾向于看曲线图。
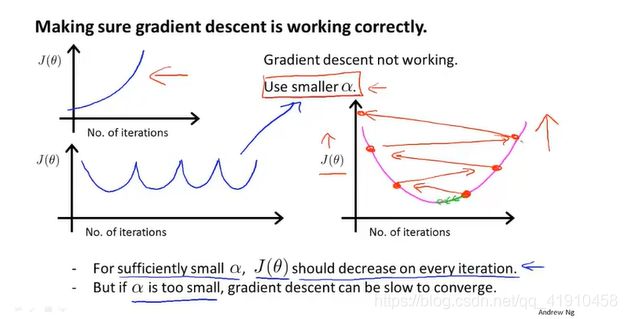
3.几种图形表示问题以及原因:
①学习率过大时:代价函数不断上升,原因 在最小化代价函数的时候选用了较大的学习率,导致越过最小值。
解决方法:选一个小的学习率。
数学家已经证明只要学习率足够小,那么每次迭代之后代价函数值都会下降,若没有下降则可能是学习率过大。
![]()
②学习率过小时:太小会收敛很慢,太大会导致不收敛
4.学习率的选择:(尝试不同的学习率,间隔10倍取值,绘制代价函数迭代次数曲线,然后比较选择可以快速下降的学习率,(通常取0.01)
可以选择个最大的,再选个最小的,在此区间,按照倍数大致取值。
4-5 特征和多项式回归 (对单特征的分析?哪些适合来进行预测?)
1.学习内容:一些可供选择的特征、如何得到不同的学习算法、多项式回归-可以用线性回归的方法来拟合非常复杂的函数或者非线性函数,如何选择某一特征,自由选择特征。
2.举例子:以预测房价为例。假设有两个特征,房子的临街的宽度和垂直宽度。但是特征的选取不一定是现有的,也可以自 己创造特征,如:特征Area 决定房屋大小的特征Area可以是宽度与深度的乘积,这样就将两个特征值预测转化为一个特征值,通过定义新的特征可能会得到一个更好的模型。
3.多项式回归模型的选择
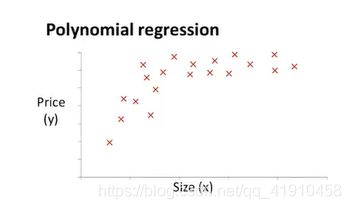
假如有这样的一个住房价格数据集,可能会有多个不同的假设函数模型用于拟合,直线不能很好的拟合这些数据,价格可能是一个二次函数所以会想到用下面的二次函数模型去拟合,但是后面价格可能会降下来,面积增大价格应该升高才对,所以二次函数也不太合适
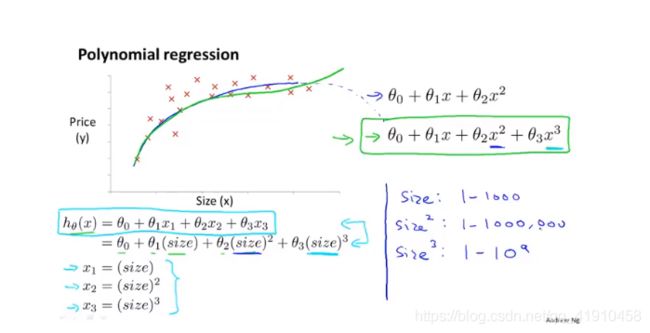
因此我们会选择一个不同的多项式模型,选择一个三次函数?可能得到下面的拟合图像合适,后面不会随着价格而下降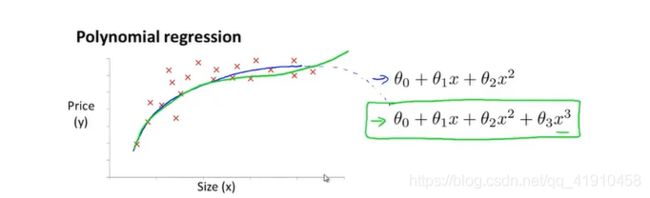
4.如何将数据与模型进行拟合?
(单一特征变量)使用(n元)一次线性回归的方法,对之前的模型简单修改即可(这里特征放缩很重要),因为这里只有一个特征值(面积预测价格),所以x变量都是面积,只是从一元线性方程,变成了三次多项式。为了将两个定义对应起来,将x1特征设为房子的面积,特征x2设置为房屋面积的平方,第三个特征x3,设为房子面积的立方,然后再利用线性回归的方法,就可以拟合这个模型,将一个(n元)三次模型拟合到数据上。
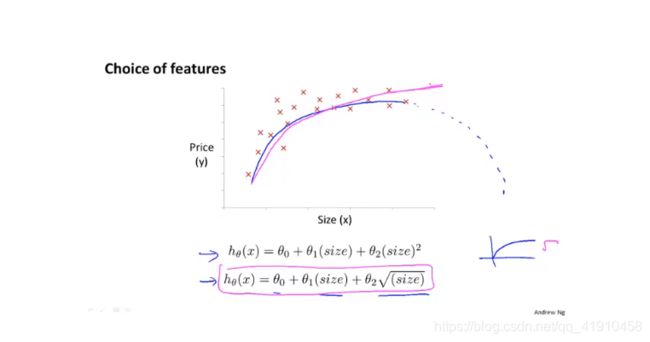
5.总结:探讨了多项式回归,如何将一个多项式回归(二次或三次函数)拟合到数据上,而不是只用一条直线去拟合(线性回归)。学习了还可以自己选择使用哪些特征。
next:有多种特征又该如何做选择?一些算法自动的选择要使用什么特征,可以观察给出的数据选择使用一次函数、二次函数、还是其他函数
4-6 正规方程(区别于迭代方法的直接解法)Normal equation 求代价函数最优参数θ
1.内容: 正规方程对于某些线性回归问题给我们更好的解决方法来求得参数θ,无需梯度下降迭代(方法1)求最小值,而是可以一次性求解参数的最优值。(只需一步)
2.举例子:最小化一个二次函数:对参数θ 求偏导数为0时的参数θ即可。
但是通常θ不是一个实数,而是一个n+1维的参数向量。代价函数通常是平方代价函数![]()
3.如何最小化这个代价函数?
①:求偏导、遍历所有的偏微分(麻烦)多次求解:逐个对参数θ求导,求J的偏导数(因为x特征值是确定的),然后全部置为0时的θ1,θ2,θ3。。。。θn的值,就得到了最小化代价函数J的θ值(这里表示一组向量),微积分基础。
②实战:矩阵最小二乘法(一次求解):这里的θ是参数向量,利用下面的方程即可得到最小值。
公式原理:线性回归_百度百科
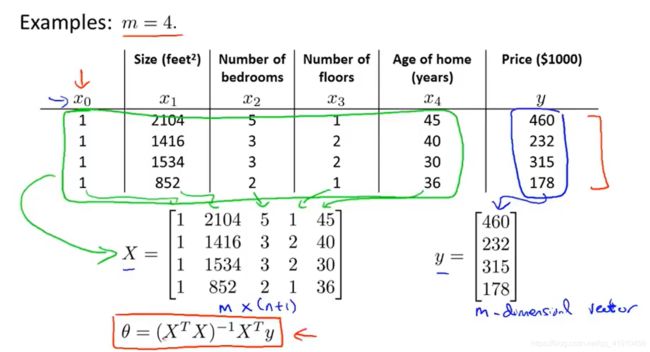
假设有4个训练样本,在数据集中加上一列,对应额外特征变量的X-0,他的取值永远是1,接下来我要做的是构建一个矩阵X(m*n+1维矩阵),这个矩阵基本包含了训练样本的所有特征变量,y是一个m维的向量。![]() 前提是矩阵可逆,一般都是可逆的, 这个等式怎么来的?(概率论与数理统计p253)
前提是矩阵可逆,一般都是可逆的, 这个等式怎么来的?(概率论与数理统计p253)
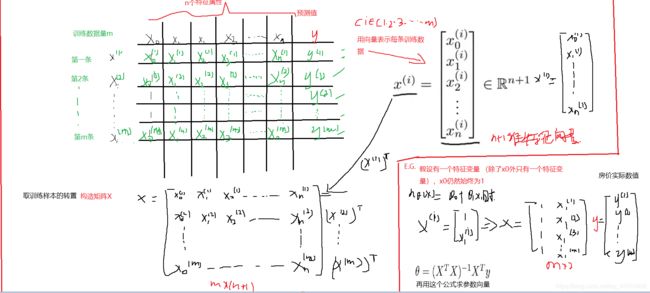
3.方程举例解释矩阵构造过程:m个样本,n个特征
 上标表示第 几个样本数据,下标表示第几个特征(先看上再读下,简单些)
上标表示第 几个样本数据,下标表示第几个特征(先看上再读下,简单些)
转化过程如下:
不需要知道怎么推导,了解是最佳求参公式即可,会给出最优的θ值。这里y是假设函数预测值
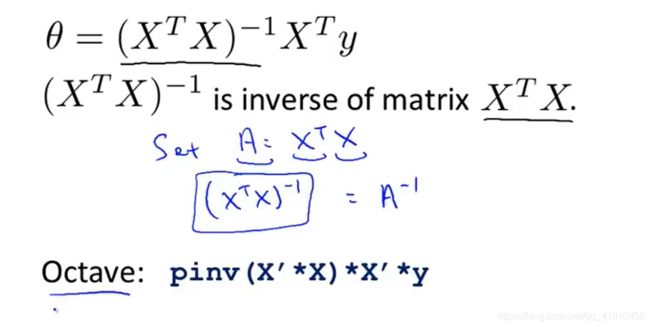 Octave代码 -----matlab计算命令代码也是类似的
Octave代码 -----matlab计算命令代码也是类似的
总结:①对比梯度下降法(必须要进行特征缩放)、正规方程法可以不进行特征缩放
②何时使用梯度下降法?何时使用正规方程法?
两者最小化参数的优缺点
1.梯度下降:
优点:在特征变量很多的情况下,也能运行的非常好。回归、分类算法都可以应用。
缺点:需要选择学习率,需要运行多次尝试不同的学习速率,才找到运行最好的那个。需要更多次的迭代,计算较慢。
2.正规方程:
优点:不需要选择学习率,只需要计算求逆的这一项,运行一次即可。也不需要迭代,不需要画出代价函数的曲线来检查收敛性。
缺点:特征变量的数量很大的话(n>10000),计算这个量会很慢O(n^3),不适合一些分类算法,复杂算法。
3.总结:特征数量大的时候选择梯度下降 在处理特征数量少(<1w)的数据集时,正规方程法比较便利,但是正规方程法不适用一些复杂的学习算法、例如逻辑回归(分类算法),不得不回归于梯度下降法,
但是对于线性(不一定是图像是直线才叫线性)回归这个特定的模型,正规方程法是比梯度下降法更快的替代算法。
4-7 正规方程在矩阵不可逆情况下的解决方法(进阶版 选学)很少发生
1.内容:正规方程及不可逆性,很少发生。
2.不可逆原因:
①存在互为线性相关的特征向量(多余 特征值一样) 导致X本身不可逆
②特征数量多 数据集少 (m 3.检查:首先检查所有的特征,看特征中是否有一些多余的特征,互为线性函数,删除其中一个,将解决不可逆问题。 特征数量过多,删除一些不影响的特征,或者考虑正规化方法。 调用内置函数哭来帮助我们做运算。 1.举例子: ①线性回归的假设函数的向量化计算:一种是计算j从0到n的乘积之和,另一种方法是用向量来表示假设函数,就可以写成计算两个向量的内积。从Xo写是为了方便计算,Xo的值为1对应参数0, 向量化的编写: C++中: ②梯度下降法的向量化计算: 假设有两个特征量,n等于2,同步更新下面的参数。 非向量化代码的实现:用个for循环来进行更新 参数解释:压缩成一行的向量化代码:将 推导过程如下: 2.总结: 使用两个以上的特征量,或在线性回归中使用几十个成千上百个特征,使用向量化实现线性回归时相比写for循环的代码更新参数时,运行的速度更快。无论是何种语言将会使你的代码更高效。
补充:5-6⭐矢量化实现线性回归。 使用向量化线性回归对比使用for循环完成的线性回归,更简洁。
 ,只需
,只需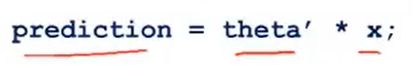 ,这一行数值线性代数代码来计算两个向量的内积。
,这一行数值线性代数代码来计算两个向量的内积。![]()
![]() 看作一个向量(n+1维),然后更新向量为
看作一个向量(n+1维),然后更新向量为![]() 减去
减去![]() (实数)乘以某个向量
(实数)乘以某个向量![]() (n+1维),因此组成了向量的减法运算。
(n+1维),因此组成了向量的减法运算。 ![]() =
=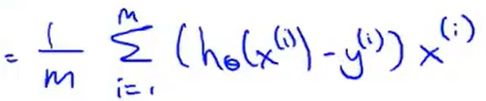 前面是一个实数不动,后面的x是一个向量。(第i个样本输入的特征值向量)
前面是一个实数不动,后面的x是一个向量。(第i个样本输入的特征值向量) 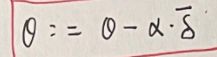 就可以利用这个公式一次更新梯度下降的参数了。与上面的更新过程是等价的
就可以利用这个公式一次更新梯度下降的参数了。与上面的更新过程是等价的