Autostitch论文翻译

摘要

本文研究的是全自动全景图像拼接问题。虽然一维问题(单轴旋转)研究得很好，但二维或多行拼接比较困难。以往的方法都是利用人工输入或对图像序列进行限制来建立匹配图像。在这项工作中，我们将拼接作为一个多图像匹配问题，并使用不变的局部特征来寻找所有图像之间的匹配。因此，我们的方法对输入图像的顺序、方向、比例和光照不敏感。它对不是全景图一部分的噪声图像也不敏感，并且可以在无序图像数据集中识别多个全景图。除了提供更多的细节，本文通过引入增益补偿和自动矫直步骤，扩展了我们之前在这一领域的工作。

1、Introduction

全景图像拼接有广泛的研究文献和一些商业应用。这个问题的基本几何已经很好地理解了，它包括估计每个图像的3×3相机矩阵或单应性。这个估计过程需要一个初始化，通常由用户输入提供，以大致对齐图像，或固定图像顺序。例如，与Canon数码相机捆绑在一起的PhotoStitch软件需要水平或垂直扫描，或图像的方阵。REALVIZ Stitcher第4版有一个用户界面，在自动注册之前，用鼠标大致定位图像。我们的工作是新颖的，因为我们不需要提供这样的初始化。
在研究文献中，自动图像对齐和拼接的方法大致分为两类——direct和基于特征的。直接方法的优点是，它们使用了所有可用的图像数据，因此可以提供非常精确的配准，但它们需要一个严密的初始化。基于特征的配准不需要初始化，但传统的特征匹配方法缺乏实现任意全景图像序列可靠匹配所需的不变性。
本文描述了一种基于不变特征的全自动全景图像拼接方法。与以前的方法相比，这种方法有几个优点。首先，我们使用不变特征使全景图像序列在输入图像旋转、缩放和照明变化的情况下能够可靠匹配。其次，将图像拼接视为多图像匹配问题，可以自动发现图像之间的匹配关系，并在无序数据集中识别全景图像。第三，我们使用多波段混合渲染无缝输出全景图来得到高质量的结果。本文通过引入增益补偿和自动矫直步骤，扩展了我们在该领域(Brown和Lowe, 2003)的早期工作。我们还描述了一个有效的束调整实现，并展示了如何执行多波段混合的多个重叠图像与任何数量的波段。
本文的其余部分结构如下。第二节阐述了这个问题的几何结构，并激发了我们对不变特征的选择。第3节描述了我们的图像匹配方法(RANSAC)和用于图像匹配验证的概率模型。在第4节中，我们描述了我们的图像对齐算法(束调整)，它联合优化每个相机的参数。第5-7节描述了渲染管道，包括自动矫直，增益补偿和多波段混合。在第9部分，我们提出了结论和对未来工作的想法。

2、Feature Matching

全景识别算法的第一步是在所有图像之间提取和匹配SIFT（Lowe，2004）特征。SIFT特征位于高斯函数差的尺度空间最大值/最小值处。在每个特征位置，建立特征尺度和方向。这提供了一个相似性不变的框架来进行测量。尽管在此帧中简单地采样强度值是相似不变的，但不变描述符实际上是通过累积方向直方图中的局部梯度来计算的。这允许边在不改变描述符向量的情况下轻微移动，从而使仿射变化具有一定的鲁棒性。这种空间累积对于平移不变性也很重要，因为兴趣点位置通常仅在0-3像素范围内精确。光照不变性是通过使用梯度（消除偏差）和归一化描述符向量（消除增益）实现的。
由于SIFT特征在旋转和尺度变化下是不变的，我们的系统可以处理不同方向和缩放的图像(见图8)。请注意，这是不可能使用传统的特征匹配技术的，如哈里斯角周围图像斑块的相关性。普通(平移)相关在旋转下不是不变的，哈里斯角在尺度变化时也不是不变的。
假设相机围绕其光学中心旋转，图像可能发生的一组变换是一组特殊的单应变换。我们用旋转矢量θ=[θ1，θ2，θ3]和焦距来参数化每个相机。这就得到了一对同源词

当

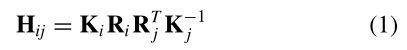
u˜i , u˜ j是对应的图像的位置（˜ui=si[ui,1]，其中ui为二维图像的位置），4参数摄像机模型定义为：

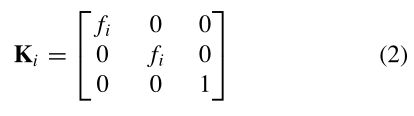
(用指数表示旋转)

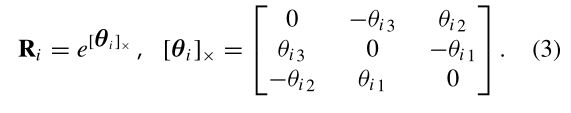
理想情况下，应该使用在这组转换下不变的图像特征。但是，对于图像位置的微小变化

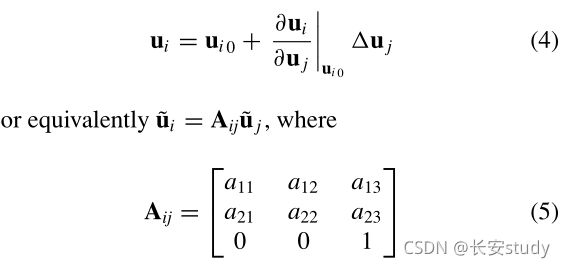
是通过线性化关于ui0的单应性得到的仿射变换。这意味着每个小图像块都经历了一个仿射变换，并证明了在仿射变化下部分不变的SIFT特征的使用是合理的。
一旦特征被从所有的图像中提取出来(线性时间)，它们必须被匹配。由于多幅图像可能重叠在一条射线上，每个特征在特征空间中被匹配到它最近邻(我们使用k=4)。这可以在O(nlogn)时间内完成，通过使用k-d树来找到近似的最近邻居(Beis和Lowe, 1997)。k-d树是一种轴对齐的二元空间分区，它递归地将特征空间按方差最大维度的均值进行分区。

3、Image Matching

在这一阶段的目标是找到所有匹配(即重叠)的图像。连接的图像匹配集稍后将成为全景图。由于每个图像都可能与其他图像相匹配，这个问题一开始似乎是图像数量的平方。然而，只需要将每个图像匹配到少量的重叠区域，来得到图像几何体的良好解。
从特征匹配步骤中，我们可以识别出它们之间存在大量匹配的图像。我们认为一个恒定的数字图像，具有最大数量的特征匹配到当前图像，作为潜在的图像匹配（我们让m＝6）。首先，我们使用RANSAC选择一组与图像之间的单应性兼容的内联线。接下来，我们应用概率模型来验证匹配。

3.1. 基于RANSAC的鲁棒单应估计

RANSAC（random sample consensus）是一种稳健的估计程序，它使用一组最小的随机抽样对应关系来估计图像变换参数，并找到与数据具有最佳一致性的解决方案。在全景图的情况下，我们选择r=4的特征对应集，并使用直接线性变换（DLT）方法计算它们之间的单应性矩阵H。我们在n=500次试验中重复这一步骤，并选择具有最大内联线数量的解决方案（在公差范围内，谁的投影与H一致），见图1。假设一对匹配图像之间的特征匹配是正确的概率（内部概率）是pi，则在n次实验之后找到正确变换的概率为

经过大量的试验，找到正确的单应性的概率是非常高的。例如，对于内点可能性pi=0.5，在500次试验后未发现正确的单应性的概率约为1×10−14。
RANSAC本质上是一种估计H的抽样方法。如果不是最大化内点数，而是最大化对数似然数的总和，结果就是最大似然估计(MLE)。此外，如果变换参数的先验是可用的，可以计算最大后验估计(MAP)。这些算法分别被称为MLESAC和MAPSAC

3.2. 图像匹配的概率模型验证

对于每一对潜在匹配的图像，我们有一组几何上一致的特征匹配(RANSAC 内点)和一组位于重叠区域但不一致的特征(RANSAC 外点)。我们验证模型的想法是比较这组嵌线/离群点由正确图像匹配或错误图像匹配生成的概率。
对于给定的图像，我们表示重叠区域的特征总数和nf和内点的数量ni。该图像匹配正确/不正确的事件由二进制变量m属于{0,1}表示。事件的特征匹配f(i)属于{0,1}是一个内点/外点假设是独立的Bernoulli贝努利事件，因此内点的总数是二项式

式中，p1是给定正确图像匹配的特征为内点的概率，p0是给定错误图像匹配的特征为内点的概率。特征匹配变量
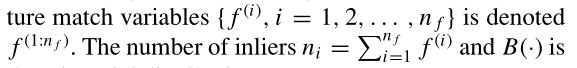二项分布

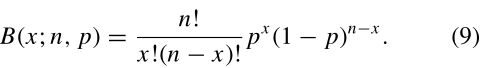
我们选择值p1=0.6和P0=0.1。现在，我们可以使用贝叶斯规则评估图像匹配正确的后验概率

对于正确的图像匹配，其中α=8.0和β=0.3。虽然在实践中，我们选择了P0、p1、p（m=0）、p（m=1）和Pmin的值，但原则上可以从数据中学习它们。例如，p1可以通过计算与大数据集上正确的同形词一致的匹配分数来估计。
一旦图像之间建立了成对匹配，我们就可以找到全景序列作为匹配图像的连接集。这使我们能够识别一组图像中的多个全景图，并拒绝与其他图像不匹配的噪声图像（见图（2））。

4、Bundle Adjustment

给定一组图像之间几何上一致的匹配，我们使用束调整（Triggs等人，1999）联合求解所有相机参数。这是一个必要的步骤，因为成对homographies的串联将导致累积错误，并忽略图像之间的多个约束，例如。G全景的两端应该连接起来。图像一个接一个地添加到捆绑调整器中，并在每个步骤中添加最佳匹配图像（一致匹配的最大数量）。新图像的初始旋转和焦距与其最佳匹配的图像相同。然后使用Levenberg-Marquardt更新参数。
我们使用的目标函数是一个鲁棒的和平方投影误差。也就是说，每个特征被投影到它匹配的所有图像中，图像距离的平方和相对于相机参数最小。(注意，也可以明确地表示未知的光线方向(实际上是统计上最优的)，并与相机参数联合估计它们。如果使用稀疏束平差方法，这并不会增加算法的复杂性(Triggs et al.， 1999)。给一对应的uki↔ulj(uk表示第k个特征在影像中的位置)，则残差为

其中，Pkij是从图像j到图像i对应的点的投影
误差函数是所有图像的鲁棒残差之和
式中n为图像个数，I(I)为与图像i匹配的图像集，F(i,j)为图像i和图像j的特征匹配集。我们使用Huber鲁棒误差函数(Huber, 1981)

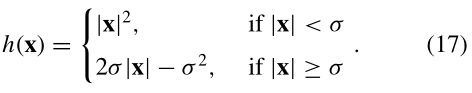
该误差函数结合了一个L2范数优化方案对内嵌点(距离小于σ)的快速收敛特性和一个L1范数优化方案对外点(距离大于σ)的鲁棒性。我们在初始化期间使用离群距离σ=∞，σ=2像素作为最终解决方案。
这是一个非线性最小二乘问题，我们用Levenberg-Marquardt算法来解决。每个迭代步骤都是这样的

当Φ是所有参数，r是残差和j =∂r/∂Φ。我们将关于参数变化的先验信念编码在(对角)协方差矩阵Cp中

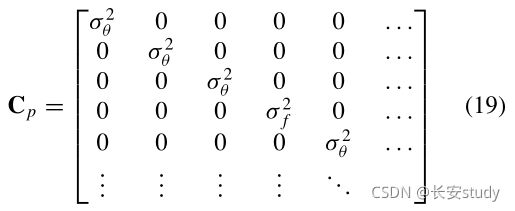
这样，角度的标准差是σθ=π/16，焦距σf=¯f/10(这里¯f是目前估计的焦距的平均值)。这有助于选择合适的步长，从而加快收敛速度。例如，如果使用球形协方差矩阵，旋转1弧度的变化与焦距参数1像素的变化一样会受到惩罚。最后，λ参数在每次迭代中都有所变化，以确保方程16的目标函数确实减小。
例如，导数是通过链式法则解析计算的

4.1. 线性系统直接计算的快速解法

由于矩阵J是稀疏的，因此将J显式地乘以它的转置是低效的。事实上，这将是束调整中最昂贵的步骤，M×N的矩阵J（Mis）的成本为（M是两次测量的数值和N是参数值）。稀疏性的产生是因为每个图像通常只与其他图像的一小部分匹配。这意味着在实践中，JTJ的每个元素都可以用远少于M的乘法进行计算

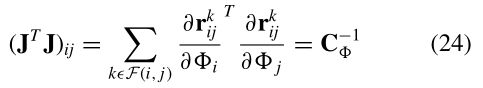
摄像机i和j之间的逆协方差仅取决于i和j之间特征匹配的残差。
类似地，JTr不能显式计算，但可以通过

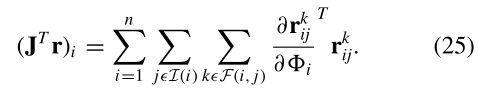
在这两种情况下，如果每个特征与每个图像匹配，则每次求和都需要乘法，但实际上，给定图像的特征匹配数远小于此数。因此，束调整是O（N3）的每次迭代，即求解N×N线性系统的成本。参数的数量是图像数量的4倍，通常是n的100倍左右。

5、自动全景校正

使用第2–4节中的步骤进行图像配准，可以获得摄像机之间的相对旋转，但对于选定的世界坐标系，仍然存在未知的3D旋转。如果我们简单地假设其中一幅图像的R=I，我们通常会在输出全景图中发现波浪效果。这是因为真正的相机不太可能完全水平和不倾斜。我们可以通过使用人们通常拍摄全景图像的方式来纠正这种波形输出，并自动拉直全景。其想法是，很少有人相对于地平线旋转相机，因此摄像机X水平轴通常位于一个平面上（见图3）。通过找到摄像机X向量协方差矩阵的零向量，我们可以找到“上向量”u（垂直于包含摄像机中心和地平线的平面）

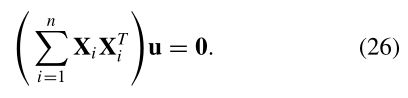
应用全局旋转，使上向量垂直（在渲染帧中）有效地从输出全景中移除波浪效果，如图4所示。

6、获得补偿

在前面的章节中，我们描述了一种计算每个摄像机的几何参数（方向和焦距）的方法。在本节中，我们将演示如何求解光度参数，即图像之间的总体增益。这是以类似的方式设置的，在所有图像上定义了一个错误函数。误差函数是所有重叠像素的增益归一化强度误差之和

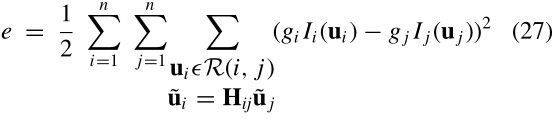
其中，gi和gj为增益，而R (i,j)为图像i与图像j的重叠区域。实际上，我们用每个重叠区域¯Iij的平均值来近似i (ui)

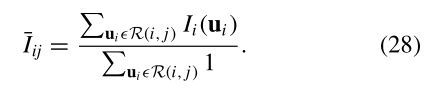
这简化了计算，并对异常值具有一定的鲁棒性，这些异常值可能是由于图像之间的小错误配准而产生的。同时，由于g=0是该问题的n个最优解，我们增加了一个前一项以保持增益接近于统一。因此误差函数为

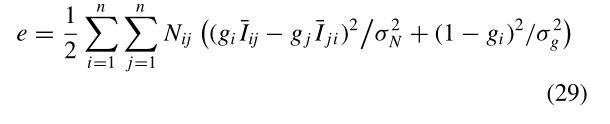
其中Nij=| R（i，j）|等于图像中重叠在图像j中的像素数。参数σN和σg分别表示归一化强度误差和增益的标准偏差。我们选择σN=10的值。（I{0…255}）和σg=0.1。这是增益参数g中的二次目标函数，可通过将导数设置为0以闭合形式求解（见图5）。

7、多波段混合

理想情况下，沿光线的每个采样（像素）在其相交的每个图像中都具有相同的强度，但实际上并非如此。即使在增益补偿之后，由于一些未建模的效果，一些图像边缘仍然可见，例如渐晕（强度朝图像边缘降低）、由于光学中心的不必要运动而产生的视差效果、由于相机的错误建模而产生的错误配准错误、径向失真等。因此，良好的混合策略非常重要。
根据前面的步骤，我们得到了n个图像Ii（x，y）（i属于{1…n}），给定已知的配准，可以用公共（球形）坐标系Ii（θ，φ）表示。为了组合来自多个图像的信息，我们为每个图像指定一个权重函数w（x，y）=w（x）w（y），其中w（x）从图像中心的1到边缘的0呈线性变化。权函数也在球坐标wi（θ，φ）中重采样。混合的一种简单方法是使用这些权重函数沿每条光线执行图像强度的加权和

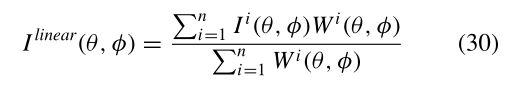
其中，线性I（θ，φ）是使用线性混合形成的合成球面图像。然而，如果存在小的配准误差，这种方法可能导致高频细节的模糊（参见图7）。为了防止这种情况，我们使用Burt和Adelson（1983）的多波段混合算法。多波段混合的思想是在大空间范围内混合低频，在短范围内混合高频。
我们通过找到图像I最负责的点集来初始化每个图像的混合权重

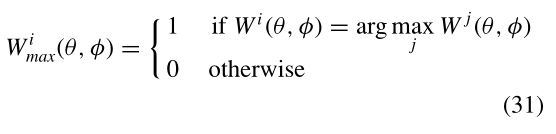
Wimax（θ，φ）是 1 f o r（θ，φ）值，其中图i为最大权重，而0为其他一些图像具有更高权重。这些最大权重贴图将连续模糊，以形成每个波段的混合权重。
形成渲染图像的高通版本

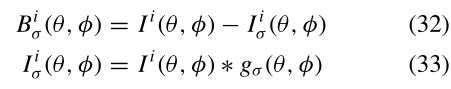
式中，gσ（θ，φ）是标准偏差σ的高斯分布∗运算符表示卷积。Bσ（θ，φ）表示波长λ范围内的空间频率λ∈[0,σ]. 我们使用模糊该图像的最大权重贴图形成的混合权重在图像之间混合该波段

式中，wiσ（θ，φ）是波长λ的混合重量λ∈[0，σ]带。使用低频带通图像混合后续频带，并进一步模糊混合权重，即。k≥1.

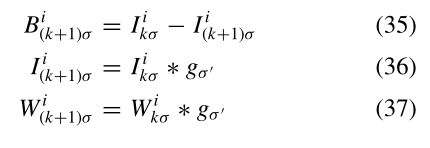
其中高斯模糊核的标准偏差σ=√（2k+1）σ的设置使得后续波段具有相同的波长范围。
对于每个波段，使用相应的混合权重线性组合重叠图像

输入： n张未排序的图像
（1）从n张图片中提取SIFT特征
（2）使用k-d树查找每个特征的K个最近邻
（3）对每张图片：
（i）选择与该图像特征匹配最多的m个候选匹配图像
（ii）利用RANSAC寻找几何一致的特征匹配，解决对图像之间的单应性
（iii）使用概率模型验证图像匹配
（4）找到图像匹配的连接组件
（5）对每个连接组件
（i）对所有的相机执行束调整，求解所有相机的旋转θ1、θ2、θ3和焦距
（ii）使用多波段混合来渲染全景
输出：全景图像

这导致高频带（小σ）在短范围内混合，而低频带（大σ）在较大范围内混合（见图（6））。
请注意，我们选择在球坐标θ，φ中渲染全景。原则上，可以选择视点周围曲面的任何二维参数化进行渲染。一个好的选择是渲染到三角形球体，在图像平面中构造混合权重。这将具有对所有图像进行统一处理的优势，而且允许简单的重采样到其他表面(在图形硬件)。注意θ，φ参数化会受到极点奇点的影响。

8、Results

全景识别算法的典型操作如图2所示。输入一组包含4张全景图和4张噪声图的图像。该算法检测匹配图像和未匹配图像的连通分量，输出4幅混合全景图。
图5显示了一个更大的示例。这组镜头是用相机的自动模式拍摄的，这种模式允许光圈和曝光时间变化，并在一些图像上使用闪光灯。尽管光照发生了这些变化，SIFT特征仍然匹配得很好，多波段混合策略产生了无缝全景图。输出是360◦×100◦度，并已渲染在球坐标(θ，φ)。所有57张图片都是完全自动匹配的，没有用户输入，并解决了4×57=228参数优化问题，最终注册。60秒内匹配并注册2272×1704像素输入图像，然后再花15分钟渲染8908×2552(2300万像素)输出全景图。2000×573的预览只用了57秒。测试是在1.6 GHz奔腾M上进行的。

9、Conclusions

本文提出了一种新颖的全自动全景拼接系统。我们使用不变局部特征和概率模型来验证图像匹配，使我们在无序图像集中识别多个全景图，并完全自动地缝合它们，无需用户输入。该系统对相机变焦、输入图像的方向和由于闪光灯曝光/光圈设置而引起的照明变化具有鲁棒性。多频带混合方案确保图像之间的平滑过渡，尽管存在照明差异，同时保留高频细节。

未来的工作

未来可能的工作领域包括对相机和场景中的运动进行补偿，以及对相机的几何和光度属性进行更高级的建模:
摄像机运动。全景图经常由于光学中心的微小运动而产生视差误差。在从中心点重新渲染之前，可以通过解决场景中的相机平移和深度问题来消除这些问题。一个好的表示方法可能是无穷远处的平面加上视差(Rother and Carlsson, 2002)。虽然相机的总体运动会造成视差伪影，但拍摄过程中的小运动会导致运动模糊。如Bascle等人(1996)所述，运动模糊图像可以使用近焦图像来消除模糊。类似的技术也可以用于生成超分辨率图像(Capel和Zisserman, 1998)。
场景运动。虽然我们的多波段混合策略在很多情况下都很有效，但在混合多幅图像时，场景中物体的大运动会造成可见的伪影(见图10)。另一种方法是根据图像之间的区域差异自动找到最佳接缝线(Davis, 1998;Uyttendaele等人，2001;Agarwala等人，2004)。
高级相机造型。大多数相机的一个重要特性是不包括在投影相机模型(保持直线)的径向畸变(Brown, 1971)。虽然我们的算法没有明确地模拟这一点，但我们已经做到了在适度的径向失真下测试了性能(见图9)。尽管在我们的实验中，全景识别和近似对齐对径向失真具有鲁棒性，但渲染结果中存在明显的伪影。因此，高质量的图像拼接应用程序需要包括径向畸变参数，至少在束调整和渲染阶段。一个理想的图像缝合器还将支持多种运动模型，例如，围绕一个点旋转(如全景图)，查看一个平面(如白板)和欧氏变换(如对齐扫描图像)。一个也可以渲染多种表面类型，例如，球形，圆柱形，平面。
光度建模。原则上，还可以估计相机的许多光度参数。渐晕（朝向图像边缘的强度降低）是伪影的常见来源，尤其是在天空等均匀颜色区域（Goldman和Chen，2005）。还可以从重叠图像区域获取高动态范围（Debevec和Malik，1997；Seetzen等人，2004）信息，并渲染色调映射或合成曝光图像。