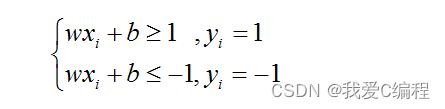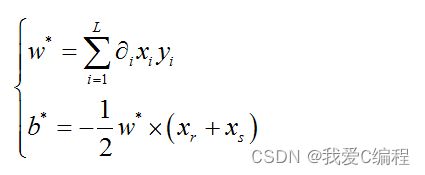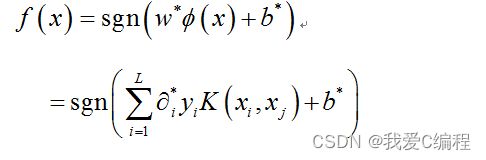m基于多核学习支持向量机MKLSVM的数据预测分类算法matlab仿真

目录

1.算法描述

2.仿真效果预览

3.MATLAB核心程序

4.完整MATLAB

---

1.算法描述

        20世纪60年代Vapnik等人提出了统计学习理论。基于该理论,于90年代给出了一种新的学习方法——支持向量机。该方法显著优点为根据结构风险最小化归纳准则,有效地避免了过学习、维数灾难和局部极小等传统机器学习中存在的弊端,且在小样本情况下仍然具有良好的泛化能力,从而该算法受到了广泛的关注。但是,随着支持向量机的不断发展和应用,其也逐渐显现出一些局限。其一,支持向量机对孤立点和噪音数据是非常敏感的。为了解决此问题,Lin等人提出了模糊支持向量机的概念,即将样例的模糊隶属度引入到支持向量机中。模糊支持向量机在一定程度上降低了噪声点和孤立点对最终决策函数的影响,提高了支持向量机的抗噪音能力。其二,核函数与核参数的选择,对学习性能有至关重要的影响,然而目前还没有关于核函数以及核参数选取的有效手段。近年来多核学习已成为机器学习领域广大学者的研究热点。即用多个核相结合来代替单个核函数。

       核方法是解决非线性模式识别的一种有效方法,它用核函数k(xi,xj)来度量样本xi和xj之间的相似性,并通过一个非线性映射将输入数据映射到高维特征空间H,然后在H中寻找线性决策边界。但传统的核方法是基于单个特征空间映射的单核学习方法,多核学习相对于传统的单核学习,有更强的可解释性和可扩展性,在解决一些实际问题时往往能够取得比单核方法更好的泛化性能。通常考虑多个基本核函数的线性凸组合是一种简单有效的多核学习方法,在该框架下,样本在特征空间中的表示问题转化为基本核与组合系数的选择问题。

       MKLSVM的核心是SVM，其大概原理如下。

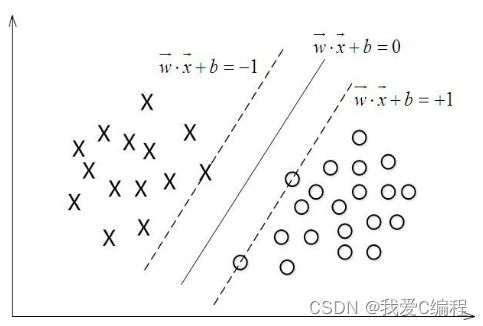
线性可分SVM分类器可以通过如下表达式来表示： 

根据公式1可知，那么SVM支持向量机的分类超平面可以表示为如下公式： 

然后通过公式2进行求解，可以得到SVM支持向量机的参数参数w和b的最优解： 

 

       在实际情况中，多数的数据属于非线性数据，那么采用上述的线性可分SVM支持向量机则无法实现数据分类，因此需要建立一个非线性的SVM支持向量机来实现数据分类。非线性可分SVM，其通过将样本数据映射到高纬度的特征空间，然后进行内积计算，得到最优分类平面。但是高纬度的特征数据内积计算降带来巨大的运算量。针对这个情况，一般采用的是一种满足Mercer 条件的核函数来实现这种内积计算，其数学公式为： 

 

因此，从而映射到高维空间后得到的最优分类函数如下所示： 

2.仿真效果预览

matlab2022a仿真结果如下：

 

 

 

3.MATLAB核心程序

.........................................................................
nbiter=8;%for循环次数
ratio=0.5;         %产生训练数据的比例，即50%训练，50%测试，
data='ionosphere' ;%选择数据类型
C = [100];%分类模型参数
verbose=1;           % 显示训练信息

options.algo='svmclass'; % Choice of algorithm in mklsvm can be either选择分类算法类型
                         % 'svmclass' or 'svmreg'
options.stopvariation=0; % use variation of weights for stopping criterion 使用权值变化作为停止准则
options.stopKKT=1;       % set to 1 if you use KKTcondition for stopping criterion    如果使用KKTcondition作为停止条件，则设置为1
options.stopdualitygap=0; % set to 1 for using duality gap for stopping criterion设为1表示使用对偶间隙作为停止准则

    options.seuildiffsigma=1e-2;        % stopping criterion for weight variation 重量变化停止准则
    options.seuildiffconstraint=0.1;    % stopping criterion for KKTKKT的停止准则
    options.seuildualitygap=0.01;       % stopping criterion for duality gap对偶间隙的停止准则

    options.goldensearch_deltmax=1e-1; % initial precision of golden section search黄金分割搜索的初始精度
    options.numericalprecision=1e-8;   % numerical precision weights below this value数值精度权重低于此值
                                       % are set to zero 
    options.lambdareg = 1e-8;          % ridge added to kernel matrix 核矩阵上的岭

    options.firstbasevariable='first'; % tie breaking method for choosing the base 断线法选基
                                       % variable in the reduced gradient method 
    options.nbitermax=500;             % maximal number of iteration  最大迭代次数
    options.seuil=0;                   % forcing to zero weights lower than this 迫使重量小于零
    options.seuilitermax=10;           % value, for iterations lower than this one 对于低于此值的迭代

    options.miniter=0;                 % minimal number of iterations最小迭代次数 
    options.verbosesvm=0;              % verbosity of inner svm algorithm 内支持向量机算法的冗余度


    options.efficientkernel=0;         % use efficient storage of kernels 

kernelt={'gaussian' 'gaussian' 'poly' 'poly' };%SVM内核参数，这个地方你需要结合SVM理论，他有一个核函数的概念呢，这里是高斯核函数
kerneloptionvect={[0.5 1 2 5 7 10 12 15 17 20] [0.5 1 2 5 7 10 12 15 17 20] [1 2 3] [1 2 3]};
variablevec={'all' 'single' 'all' 'single'};


classcode=[1 -1];%分类识别码，即1和-1两种类型
load([data ]);%用laod函数加载数据
[nbdata,dim]=size(x);%数据的长度和深度

nbtrain=floor(nbdata*ratio);%根据ratio变量得到训练参数
rand('state',0);%随机化因子0，以0位随机随机状态开始训练。

for i=1: nbiter
    i
    %这个地方产生训练数据和测试数据，具体见CreateDataAppTest内部函数的注释
    %输入原始的数据x和y，训练比例，分类编码，输出训练xy，测试xy
    [xapp,yapp,xtest,ytest,indice]=CreateDataAppTest(x, y, nbtrain,classcode);
    % [xapp,xtest]=normalizemeanstd(xapp,xtest);
    %这个是产生SVM核，具体见CreateKernelListWithVariable子函数注释
    %输入的参数就是前面注释的核函数参数
    %输出的变量函数是核类型，核参数，核变量
    [kernel,kerneloptionvec,variableveccell]=CreateKernelListWithVariable(variablevec,dim,kernelt,kerneloptionvect);
    %这个变量的功能是归一化操作，具体见UnitTraceNormalization里面的参数
    %输入的参数是数据xapp以及核参数
    %输出的是初始权值和核参数信息。
    [Weight,InfoKernel]=UnitTraceNormalization(xapp,kernel,kerneloptionvec,variableveccell);
    
    %根据得到的初始的核信息参数，得到对应的参数K，这个K的功能是SVM中的包含所有Gram矩阵的矩阵
    K=mklkernel(xapp,InfoKernel,Weight,options);
 
    tic
    %开始进行SVM训练，具体见mklsvm函数的内部注释
    [beta,w,b,posw,story(i),obj(i)] = mklsvm(K,yapp,C,options,verbose);
    timelasso(i)=toc%配合tic，toc计算SVM训练时间
    
    
    %这个部分开始测试，使用前面训练得到的参数对新的测试数据进行测试。
    Kt=mklkernel(xtest,InfoKernel,Weight,options,xapp(posw,:),beta);
    ypred=Kt*w+b;%这个是标准的SVM的识别输出公式，word中有介绍。

    bc(i)=mean(sign(ypred)==ytest)%计算误差

end;%
tt2=story.KKTconstraint
05_100_m

4.完整MATLAB

V