【AI】神经网络算法的本质(04)
目录
1、神经网络的本质(复合函数)
1.1 神经网络的任务
1.2 线性神经网络例子
2、损失函数(对数函数)
2.1 损失函数的本质
2.2 损失函数举例
2.3 前向传播
1、神经网络的本质(复合函数)
如果非要用一句话概括神经网络,我找到了一句比较合适的句子:一个多层的复合函数:
人工神经网络在本质上是一个多层的复合函数,它实现了从向量x到向量y的映射。以前不叫神经网络,叫线性回归,或者逻辑回归;
1.1 神经网络的任务
神经网络的任务有2个
1) 特征提取:把特征变换成一个向量
2)更新权重:更新特征的权重,找到合适的权重
神经网络的输入数据,都有他自己的特征,如何提取出这些特征,并将它用好这个特征,是我们需要关注的。其实AI最核心的,也是怎么利用这些特征,来求得权重参数。是通过调大、还是调小,调试的结果对结果有什么影响,这个是我们要学习的。
1.2 线性神经网络例子
我们举个简单的例子来理解神经网络计算的过程,我们的目标是:构建一个模型,让这个模型能够识别猫,给定一张图片,就能判断出来是不是猫、还是狗、还是汽车。现在给定一张有猫的图片(猫), 并且刻画出这个猫的特征,我们就把这个猫的特征描述为4个点:
56 , 231
2 4 , 2
为了方便计算,我们把它变成一列:Xi,同时呢,我们也给定一个随机的权重W(后面会不断的更新),他是3*4的矩阵(3行:便是要得到3个分类结果当做RGB通道,4便是猫的4个特征的数值,通过权重参数和特征做组合来构建网络结构),然后在加上偏置b(这个偏置的维度也是和输出是保持一致的),其实识别猫,就是根据猫的特征,不断计算,找出更能刻画猫的特诊的权重W 。为了方便理解,假定他是 y=Wx+b, 一个非常普通的线性方程。通过这个方程,找出合适的W和b,进而可以计算出预测的结果 ,先给出一个随机的W,然后计算出分类结果,再根据分类结果和标准结果比较,看看他们偏差多少,进而调整W,直到损失最小。
这个我们给出了一个随机的w,就可以计算出他的结果,那这个结果和标准的偏差大么,那就得看损失函数了。
2、损失函数(对数函数)
2.1 损失函数的本质
本质:预测值和真实值之间的差异,就是损失。损失是怎么得到的呢?以分类任务为例,我们通过上面的一顿骚操作,得到at,car,frog,分别计算出来的预测值是[3.2,5.1,-1.7]。我们预测得到一个预测数值,但是他们的差异并不大,为了让他们做一个更好的区分。我们做一个映射,让差异体现的更加明显一点。 我们通过e的x次方来放大,得到:[24.5,164,0.18]。
在进一步思考,其实分类的目标,我们想要的得到是一个概率值 ,并不是上面计算得到的一个数值。那如何得到规律值呢?做归一化:上面三个数值的求和,然后数值除以这个和,就求出了各自的概率值了,由一个数值,得到了一个概率值。
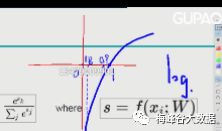
在进一步思考,虽然我们又概率值了,但是我们要更新w,我们的得知道他和标准结果的差异在哪,也就是要计算出损失,这个又怎么算呢。我们来看一个函数,进一步了理解损失函数的本质:和正确值概率的偏差,和对数函数如出一辙。所以经常用对数函数来求损失,对数函数如下:他和x的交点为(1,0),概率值的取值范围就是0-1之间,而我们关注的是属于正确类别的概率是多少。
2.2 损失函数举例
假设预测一只猫,如果概率不是100%,那他就有损失。属于正确的概率,如果和标准没有差异,他的损失就是0。假如预测是0.9,看下面这个图,那他的损失y就会很小,如下图所示,如果他预测是0.01,那他的损失就大,所以用对数函数log来表述损失函数看上去非常好。
下面这个例子,把流程一起来串一遍:
第一步:差异放大,通过e的x次方将差异放大,预测结果从3.2,5.1,-1.7映射为24.5,164,0.18
第二步:归一化,得到分类的规律值,通过求和,计算占比概率,得到:0.13,0.87,0.0
第三步:计算损失值,公式如下
X=3.2时,损失值为:-log(0.13)=0.886
x=164时,损失值为:-log(164)= -2.2
x=0 时,损失值为:无穷大
2.3 前向传播
其实神经网络的任务,并不是为了计算损失, 算损失的目的是,如何通过损失来调整W权重参数,分析出哪个W导致的损失,然后不断优化他,指导损失最小。如何通过损失来更新w,这个其实就是反向传播。如何通过输入,来计算损失,这个是前向传播,最终目的优化W参数,让让损失越来越小。
写着写着,有点困了,止笔,后面接着将有趣的梯度下降、卷积神经网络。
备注:相关素材来源于唐宇迪博士,特别鸣谢,更多AI文章请关注VX公众号
收录于合集 #计算机视觉学习
6个
上一篇【AI】当传统算法碰到计算机视觉(03)下一篇【AI】梯度下降的数学原理(05)