使用傅里叶变换过滤时间序列（轴承数据）噪声

1  将轴承数据使用傅里叶变换过滤噪声后，再还原成时序数据

# 傅里叶变换过滤时间序列噪声
# 点击“算法数据侠”，“星标”公众号

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
#%matplotlib inline
import os
import pandas as pd
plt.rcParams['figure.figsize'] = [16, 10]
plt.rcParams.update({'font.size': 18})

导入模块

 数据长这样子：

一共16384个数据点，即time为0~16383

#data = pd.read_csv("E:/wulihua/LSTM/CODE/file7.csv", header=None)  #必须添加header=None，否则默认把第一行数据处理成列名导致缺失
data = pd.read_csv("E:/wulihua/LSTM/CODE/file7.csv")  # 读的是矩阵datafram格式的
features_considered = ['data_number']
features = data[features_considered]   # 得到这一列的数据，格式为datafarm
features.plot(subplots=True)           # 画了图看一下
features = features.values.tolist()    # 将矩阵datafarm转换成列表list
features = np.array(features)          # 将列表list转换成数组nadarry,维度为18640，里面一个元素
print(features)
print(type(features))
print(features.shape)
t4 =features.flatten()  # 将多维展成一维的数组
print(type(t4))
print(t4.shape)

 因为pd.read_csv读的是矩阵datafram格式，而后面傅里叶函数函需要用nadarry类型。

datafram类型------list列表-----nadarry数组

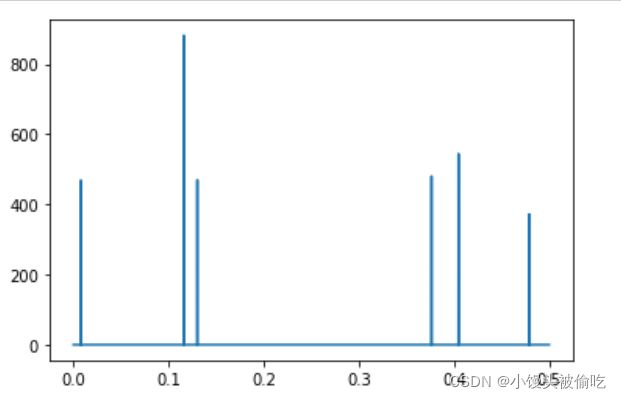
时频转换在代码中，这里使用rfft而不是fft。r意味着reduce只计算正频率。所有负镜像频率将被省略。因为它的速度更快。
rfft函数的yf结果是一个复数，形式类似于a+bj。np.abs()函数将为复数计算√(a² + b²)。下面是原始波的神奇的频域视图，x轴表示频率。

from scipy.fft import rfft, rfftfreq
t = np.arange(start=0, stop=16384, step=data_step)      # 时间
data_step = 1
print(type(t))
n = len(t)
yf = rfft(t4)
xf = rfftfreq(n, data_step)
plt.plot(xf, np.abs(yf))
plt.show()

 

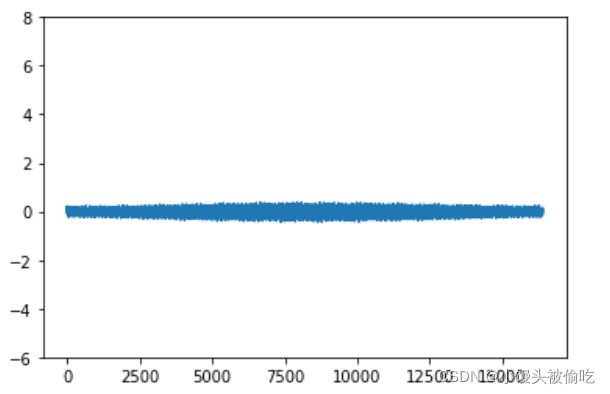
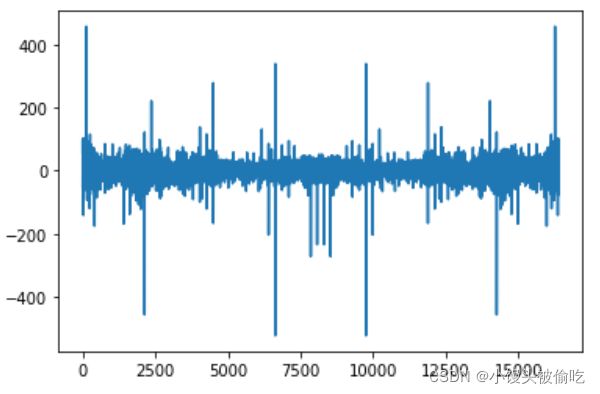
# 过滤噪声频率,在Numpy的帮助下，我们可以很容易地将这些频率数据设置为0，除了50Hz和120Hz。
yf_abs = np.abs(yf)
indices = yf_abs>300# filter out those value under 300
yf_clean = indices * yf # noise frequency will be set to 0
plt.plot(xf, np.abs(yf_clean))
plt.show()

# 最后一步就是逆转换了，将频域数据转换回时域数据。结果表明，所有的噪声波都被去除了。
from scipy.fft import irfft
new_f_clean = irfft(yf_clean)
plt.plot(t, new_f_clean)
plt.ylim(-6, 8)   # 8控制噪声范围，数值越大，赋值越大
plt.show()

 

 2 对轴承数据进行傅里叶变化

2.1 使用自定义的傅里叶函数对轴承数据进行傅里叶变化

#data = pd.read_csv("E:/wulihua/LSTM/CODE/file7.csv", header=None)  #必须添加header=None，否则默认把第一行数据处理成列名导致缺失
data = pd.read_csv("E:/wulihua/LSTM/CODE/file7.csv")  # 读的是矩阵datafram格式的
features_considered = ['data_number']
features = data[features_considered]   # 得到这一列的数据，格式为datafarm
features.plot(subplots=True)
features = features.values.tolist()    # 将矩阵datafarm转换成列表list
features = np.array(features)          # 将列表list转换成数组nadarry,维度为18640，里面一个元素
print(features)
print(type(features))
print(features.shape)
t4 =features.flatten()  # 将多维展成一维的数组
print(type(t4))
print(t4.shape)



# 使用自定义的傅里叶变化进行傅里叶变换
import numpy as np
from scipy.fft import fft
def DFT_slow(x):
    x = np.asarray(x, dtype=float)# ensure the data type
    N = x.shape[0]                # get the x array length
    n = np.arange(N)              # 1d array
    k = n.reshape((N, 1))       # 2d array, 10 x 1, aka column array
    M = np.exp(-2j * np.pi * k * n / N)
    return np.dot(M, x)       # [a,b] . [c,d] = ac + bd, it is a sum,返回的是M和x的内积
#x = np.random.random(1024)
#print(np.allclose(DFT_slow(x), fft(x)))    # 比较两个array是不是每一元素都相等，默认在1e-05的误差范围内,输出true说明是和内置的一样
a=DFT_slow(t4) # 返回的是M和x的点积
plt.plot(a)

 

 

2.2 使用系统自带的傅里叶函数对轴承进行傅里叶变换

#data = pd.read_csv("E:/wulihua/LSTM/CODE/file7.csv", header=None)  #必须添加header=None，否则默认把第一行数据处理成列名导致缺失
data = pd.read_csv("E:/wulihua/LSTM/CODE/file7.csv")  # 读的是矩阵datafram格式的
features_considered = ['data_number']
features = data[features_considered]   # 得到这一列的数据，格式为datafarm
features.plot(subplots=True)
features = features.values.tolist()    # 将矩阵datafarm转换成列表list
features = np.array(features)          # 将列表list转换成数组nadarry,维度为18640，里面一个元素
print(features)
print(type(features))
print(features.shape)
t4 =features.flatten()  # 将多维展成一维的数组
print(type(t4))
print(t4.shape)


# 使用系统自带的傅里叶函数将进行傅里叶变换
# fft 计算一维n-point离散傅立叶变换
b = fft(t4)   # 返回的是点积，具体内容看自定义傅里叶函数，两个是一样的
plt.plot(b)