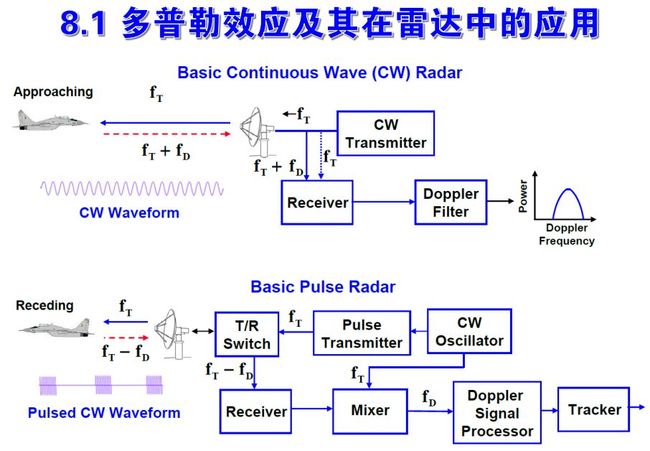
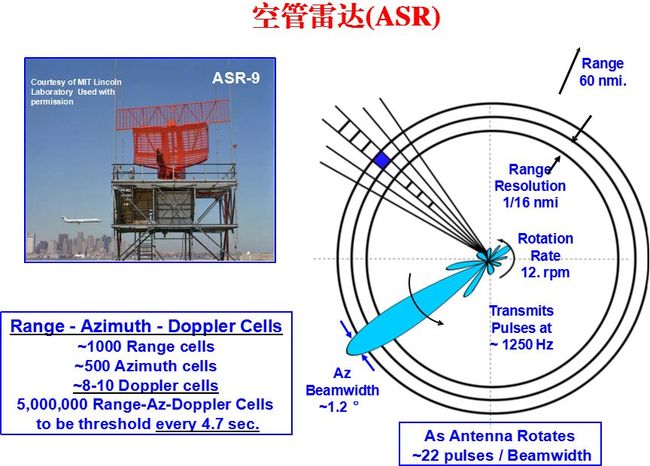
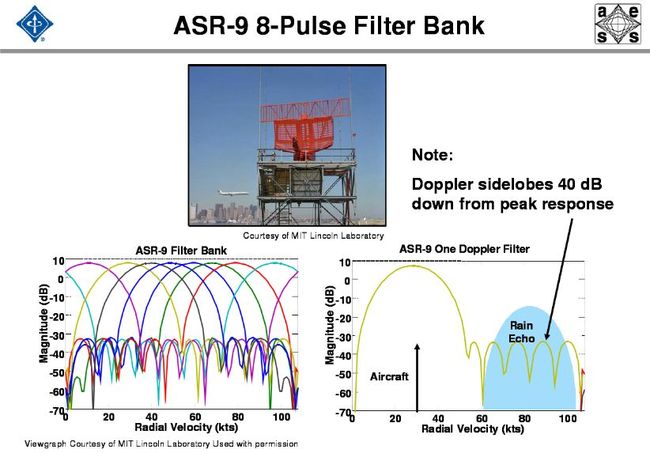
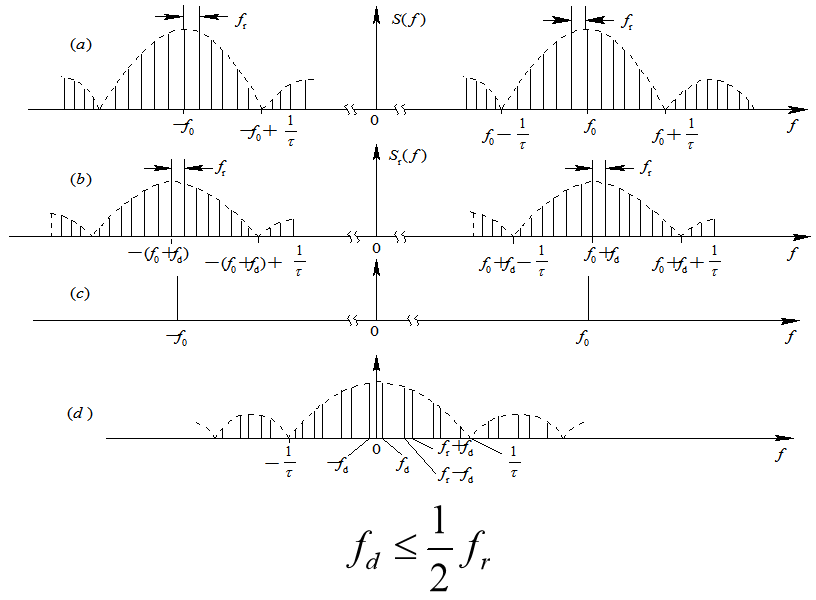c++实现超声回波包络检测_雷达原理与系统第八章 运动目标检测
式中, ω0为发射角频率, φ为初相; A为振幅。
式中, tr = 2R/c, 为回波滞后于发射信号的时间, 其中R为目标和雷达站间的距离; c为电磁波传播速度, 在自由空间传播时它等于光速; k为回波的衰减系数。
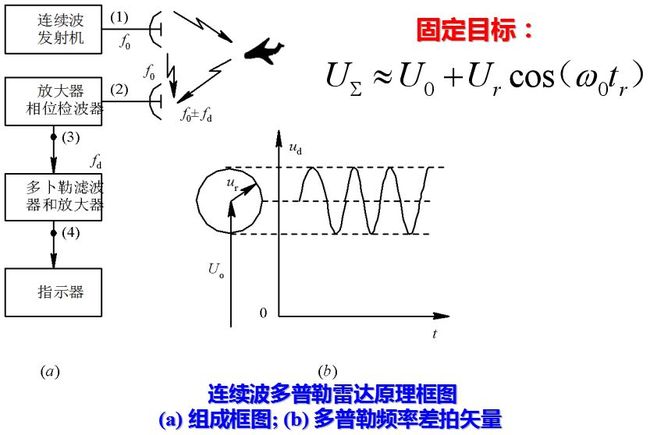
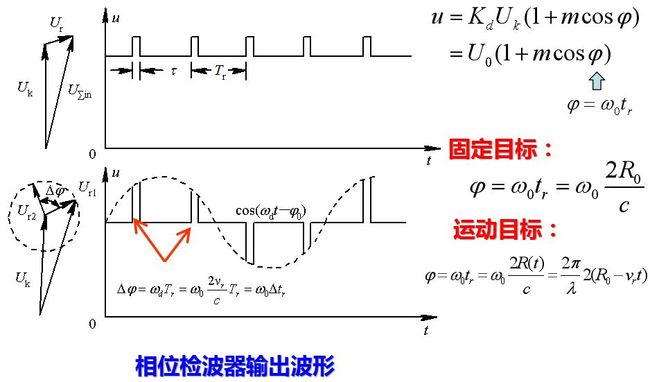
如果目标固定不动, 则距离R为常数。回波与发射信号之间有固定相位差ω0tr=2πf0·2R/c = (2π/λ) 2R, 它是电磁波往返于雷达与目标之间所产生的相位滞后。
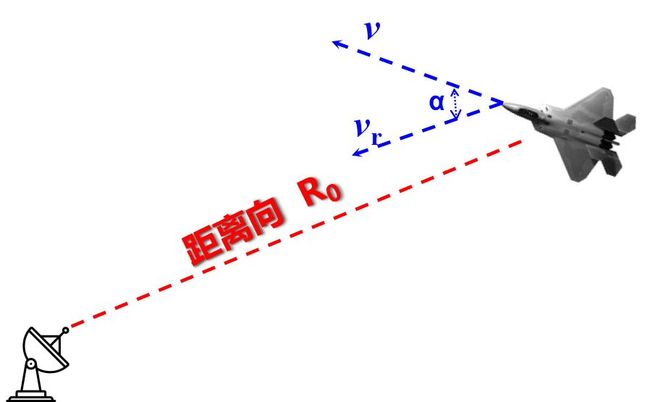
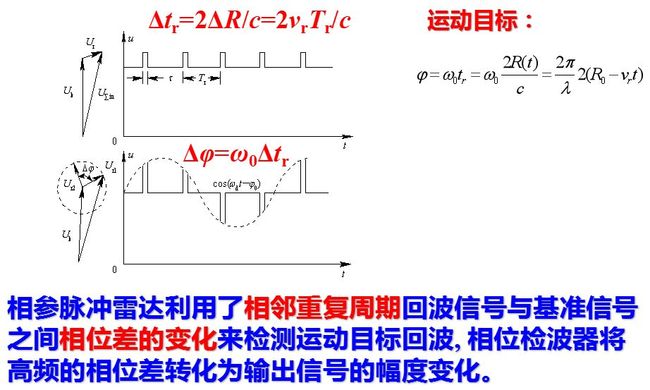
当目标与雷达站之间有相对运动时, 则距离R随时间变化。设目标以匀速相对雷达站运动, 则在时间t时刻, 目标与雷达站间的距离R(t)为。式中,R0 为 t=0 时的距离;vr为目标相对雷达站的径向运动速度。
在t时刻接收到的波形sr(t)上的某点, 是在t-tr时刻发射的。由于通常雷达和目标间的相对运动速度vr远小于电磁波速度c, 故时延tr可近似写为
是时间t的函数, 在径向速度vr为常数时, 产生频率差,这就是多普勒频率, 它正比于相对运动的速度而反比于工作波长λ。当目标飞向雷达站时, 多普勒频率为正值, 接收信号频率高于发射信号频率, 而当目标背离雷达站飞行时, 多普勒频率为负值, 接收信号频率低于发射信号频率。
多普勒频率可以直观地解释为: 振荡源发射的电磁波以恒速c传播, 如果接收者相对于振荡源是不动的, 则他在单位时间内收到的振荡数目与振荡源发出的相同, 即二者频率相等。如果振荡源与接收者之间有相对接近的运动, 则接收者在单位时间内收到的振荡数目要比他不动时多一些, 也就是接收频率增高;当二者作背向运动时, 结果相反。
常用雷达信号为窄带信号(带宽远小于中心频率)。其发射信号可以表示为
式中,Re表示取实部; u(t)为调制信号的复数包络; ω0为发射角频率。
同连续波发射时的情况相似, 由目标反射的回波信号sr(t)可以写成上式。
当目标固定不动时, 回波信号的复包络有一固定迟延, 而高频则有一个固定相位差。
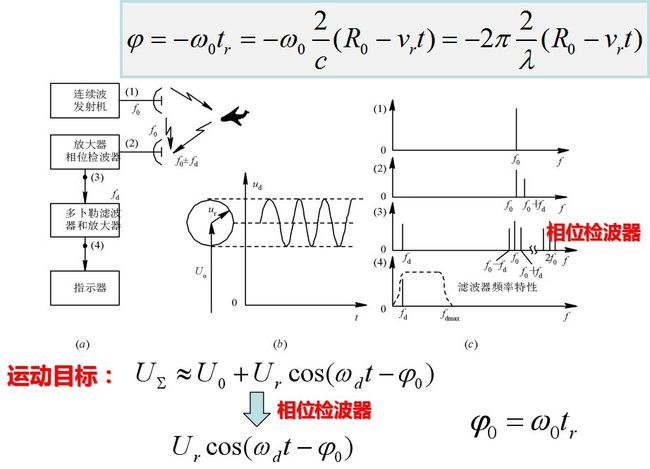
则式的回波信号表示式说明, 回波信号比起发射信号来讲, 复包络滞后tr, 而高频相位差φ=-ω0tr=-2π (2/λ)(R0-vrt)是时间的函数。当速度vr为常数时, φ(t)引起的频率差为fd,称为多普勒频率, 即回波信号的频率比之发射频率有一个多普勒频移。
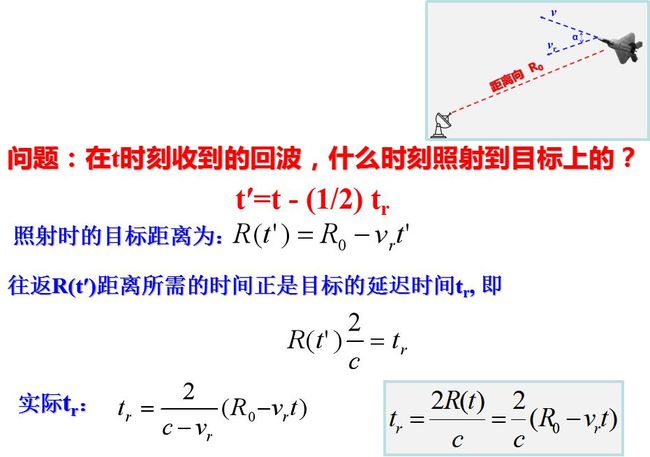
较严格地讨论运动目标回波的特点。在t时刻收到的回波是在t-tr时刻发射的, 而照射到目标上的时间是t′=t - (1/2) tr, 照射时的目标距离为上式所示。
即信号角频率的变化值ωd = (2vr/c) ω0 = 2π 2vr/λ, 为多普勒频移。近似后的结果, 与常用的多普勒频率表达式相同。对于窄带发射信号而言, 要严格地讨论运动目标回波的特点, 得到的结果是如上式。
中的因子(c+vr)/(c-vr)表示信号在时间轴上的增长或压缩。根据目标运动的方向可确定其是增长还是压缩。目标和雷达站相对运动时, vr为正值, 相当于波形在时间轴上压缩, 而在频率轴上频谱将展宽。
但在雷达的大多数应用情况下, 上述复包络变化的效应可以忽略。
这个条件是经常满足的, 例如若目标速度为10倍音速, vr=3.3×103 m/s, 则2vr/c≈ 2×10-5, 这样即使信号的时间带宽积τΔf为1000数量级时, 不等式仍能满足。以上讨论均忽略了目标加速度引起的影响。可以看出, 在当前目标运动的速度范围内, 运动目标回波的表达式可以近为上式。,
运动目标回波的主要特征是其中心频率偏移多普勒频率, 其它影响均可忽略。前面近似结果完全可以实用。
回波信号产生的多普勒频移可由发射站到目标的距离Rt加上由目标到接收站的距离Rr随时间变化求得,在单基地雷达情况下, 引起多普勒频移的是雷达和目标连线方向的径向速度vr。设目标运动方向与该连线的夹角为α, 目标速度为v, 则径向速度分量vr为vcos(α)。
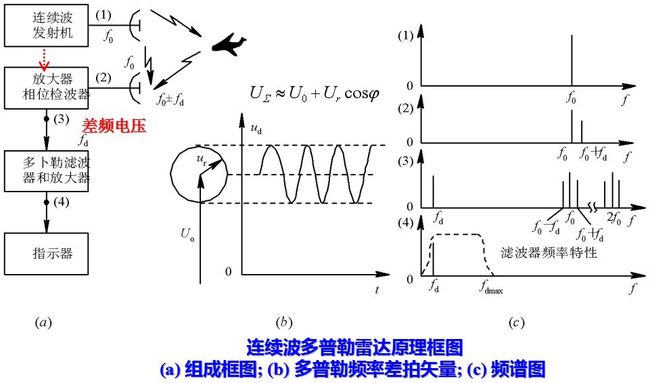
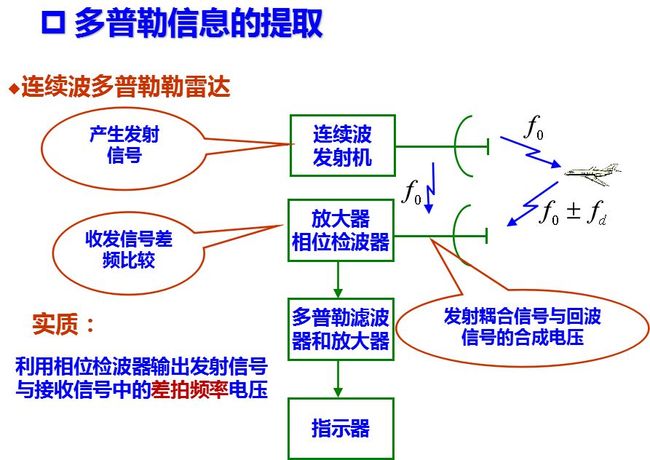
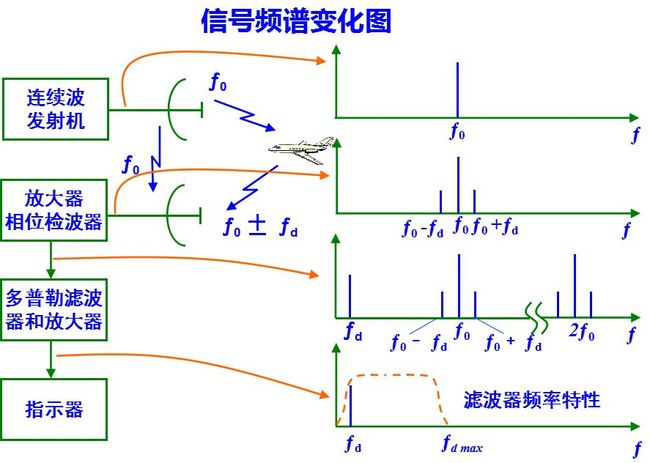
已经知道, 回波信号的多普勒频移fd正比于径向速度,而反比于雷达工作波长λ, 即多普勒频移的相对值正比于目标速度与光速之比, fd的正负值取决于目标运动的方向。在多数情况下, 多普勒频率处于音频范围。例如当λ= 10 cm, vr= 300 m/s时, 求得fd = 6kHz 。而此时雷达工作频率f0 = 3000MHz , 目标回波信号频率为fr = 3000 MHz±6kHz, 两者相差的百分比是很小的。因此要从接收信号中提取多普勒频率需要采用差拍的方法, 即设法取出f0和fr的差值fd 。
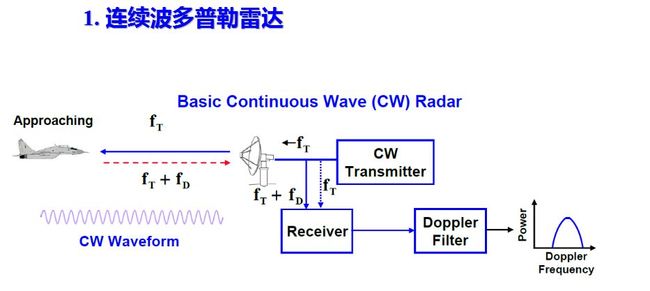
发射机产生频率为f0的等幅连续波高频振荡, 其中绝大部分能量从发射天线辐射到空间, 很少部分能量耦合到接收机输入端作为基准电压。混合的发射信号和接收信号经过放大后, 在相位检波器输出端取出其差拍电压, 隔除其中直流分量, 得到多普勒频率信号送到终端指示器。
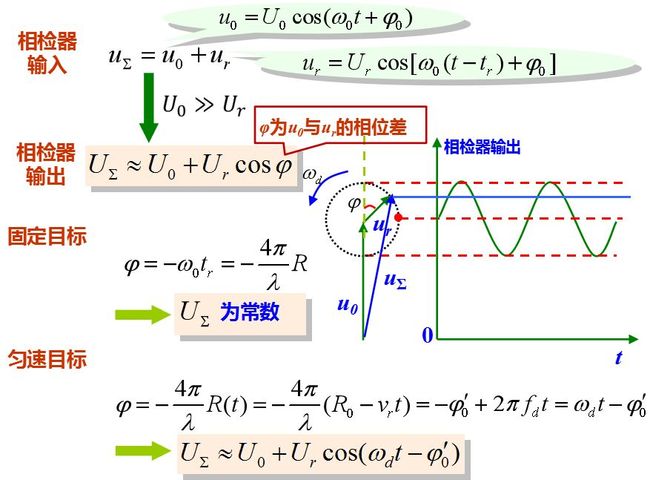
对于固定目标信号, 由于它和基准信号的相位差φ=ω0tr保持常数, 故混合相加的合成电压幅度亦不改变。当回波信号振幅Ur远小于基准信号振幅U0时, 从矢量图上可求得其合成电压。
而运动目标回波与基准电压的相位差随时间按多普勒频率变化。即回波信号矢量围绕基准信号矢量端点以等角速度ωd旋转, 这时合成矢量的振幅为
经相位检波器取出二电压的差拍, 通过隔直流电容器得到输出的多普勒频率信号为上式。
在检波器中, 还可能产生多种和差组合频率, 可用低通滤波器取出所需要的多普勒频率fd送到终端指示(例如频率计), 即可测得目标的径向速度值。
在检波器中, 还可能产生多种和差组合频率, 可用低通滤波器取出所需要的多普勒频率fd送到终端指示(例如频率计), 即可测得目标的径向速度值。
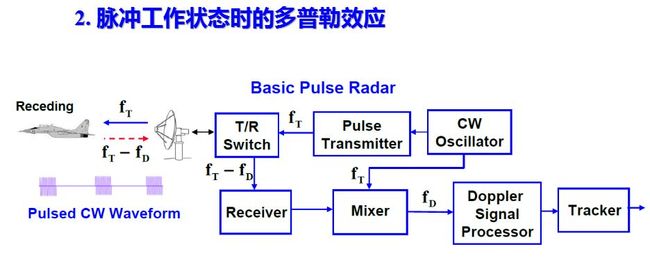
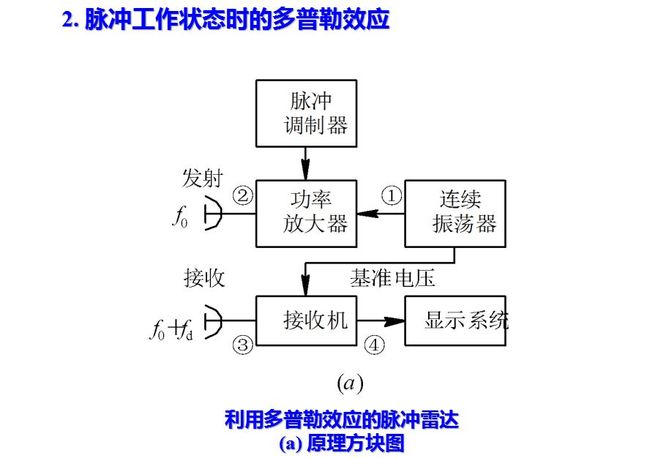
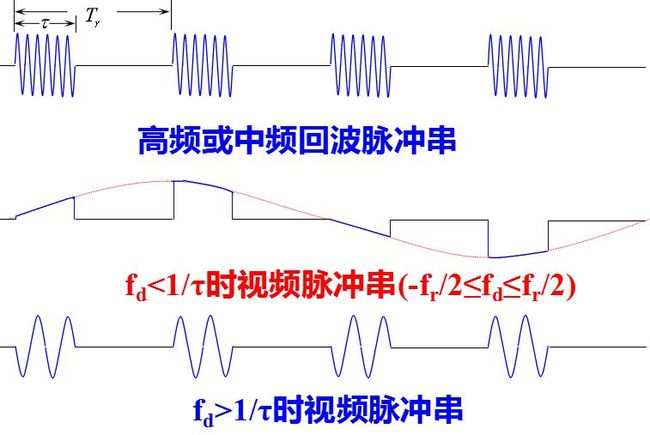
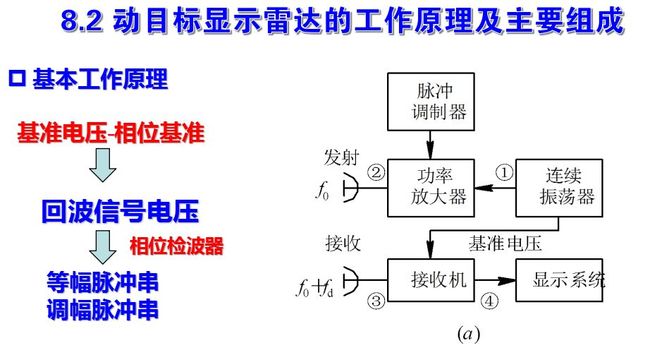
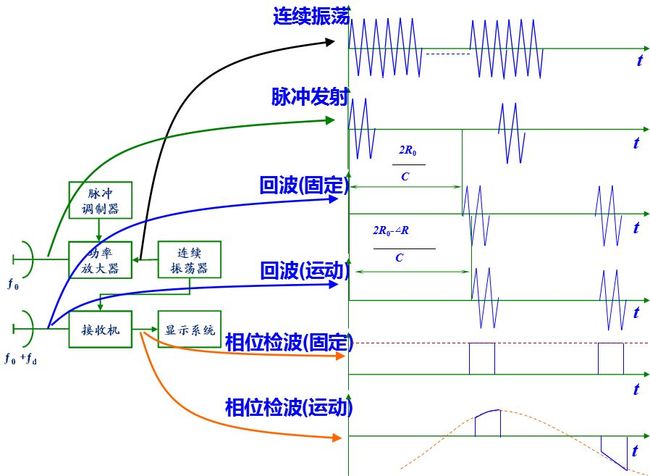
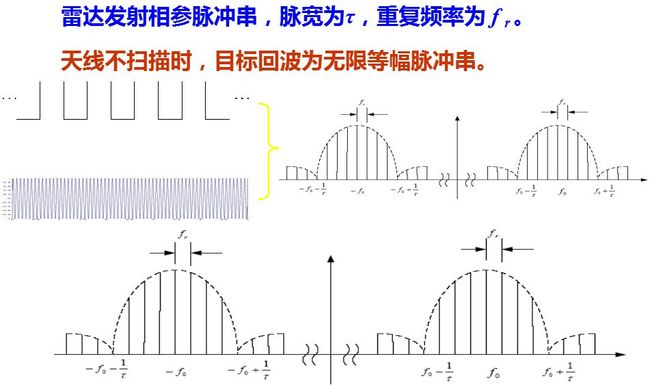
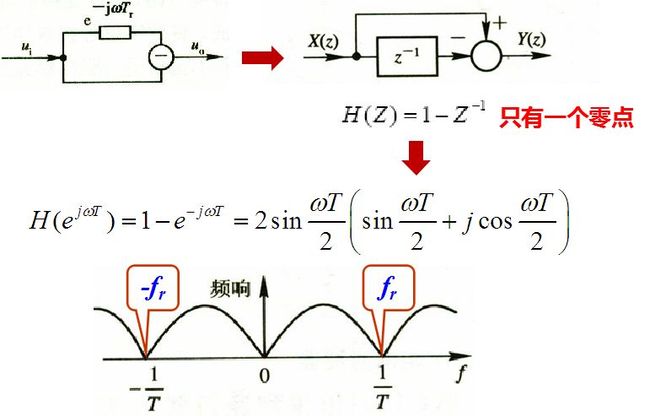
脉冲雷达是最常用的雷达工作方式。当雷达发射脉冲信号时, 和连续发射时一样, 运动目标回波信号中产生一个附加的多普勒频率分量。所不同的是目标回波仅在脉冲宽度时间内按重复周期出现。
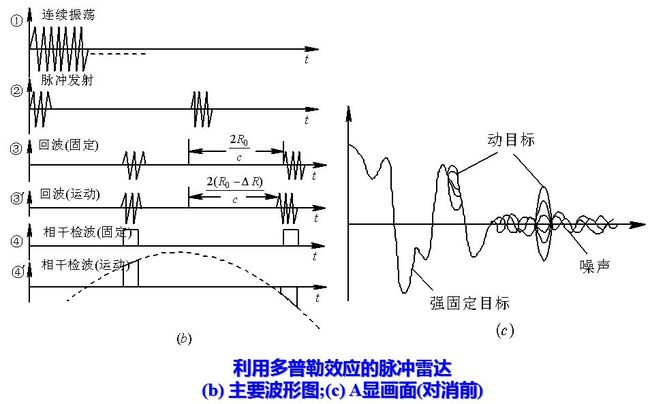
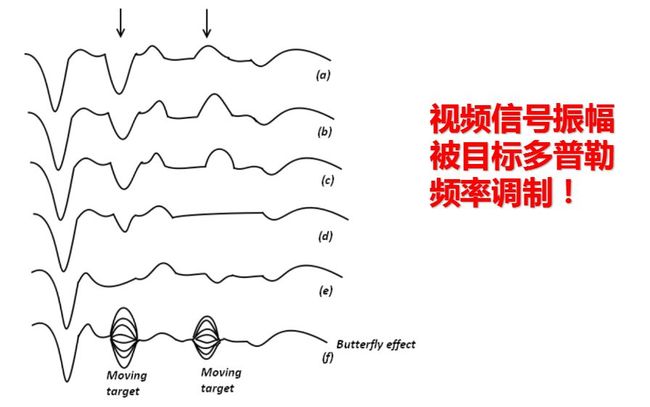
图画出了利用多普勒效应的脉冲雷达方框图及各主要点的波形图, 图中所示为多普勒频率fd小于脉冲宽度倒数的情况。
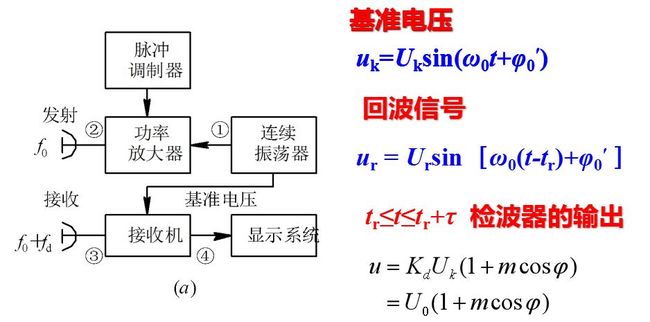
和连续波雷达的工作情况相类比: 发射信号按一定的脉冲宽度τ和重复周期Tr工作。由连续振荡器取出的电压作为接收机相位检波器的基准电压, 基准电压在每一重复周期均和发射信号有相同的起始相位, 因而是相参的。
相位检波器输入端所加电压有两个: 连续的基准电压uk,uk=Uksin(ω0t+φ0′), 其频率和起始相位均与发射信号相同; 回波信号ur, ur = Ursin[ω0(t-tr)+φ0′ ], 当雷达为脉冲工作时, 回波信号是脉冲电压, 只在信号来到期间即tr≤t≤tr+τ时才存在, 其它时间只有基准电压Uk加在相位检波器上。经过检波器的输出信号为上式所示。
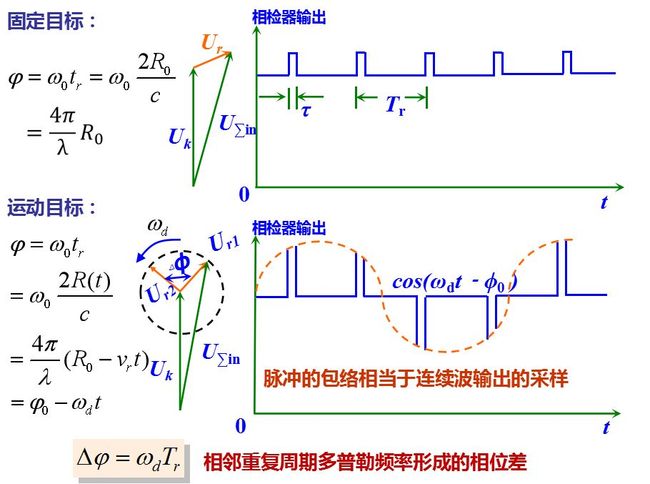
式中, U0为直流分量, 为连续振荡的基准电压经检波后的输出, 而U0m cos φ则代表检波后的信号分量。在脉冲雷达中, 由于回波信号为按一定重复周期出现的脉冲, 因此, U0m cosφ表示相位检波器输出回波信号的包络。图8.3给出了相位检波器输出波形图。对于固定目标来讲, 相位差φ是常数, 合成矢量的幅度不变化, 检波后隔去直流分量可得到一串等幅脉冲输出。
对运动目标回波而言, 相位差随时间t改变, 其变化情况由目标径向运动速度vr及雷达工作波长λ决定。
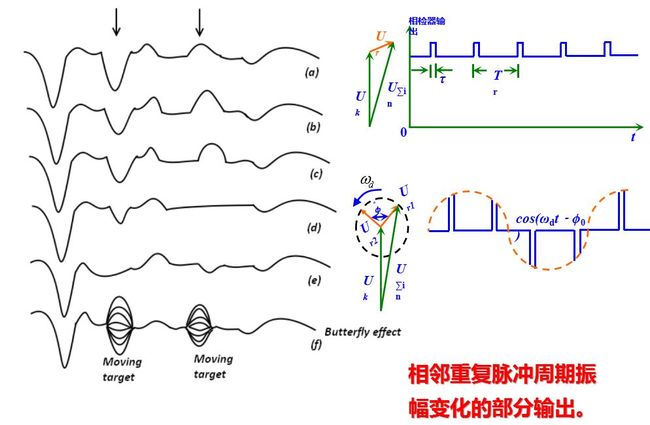
相邻重复周期延迟时间的变化量Δtr=2ΔR/c=2vrTr/c是很小的数量, 但当它反映到高频相位上时, Δφ=ω0Δtr就会产生很灵敏的反应。相参脉冲雷达利用了相邻重复周期回波信号与基准信号之间相位差的变化来检测运动目标回波, 相位检波器将高频的相位差转化为输出信号的幅度变化。脉冲雷达工作时, 单个回波脉冲的中心频率亦有相应的多普勒频移, 但在fd<<1/τ的条件下(这是常遇到的情况), 这个多普勒频移只使相位检波器输出脉冲的顶部产生畸变。这就表明要检测出多普勒频率需要多个脉冲信号。只有当fd >1/τ时, 才有可能利用单个脉冲测出其多普勒频率。对于运动目标回波, 其重复周期的微小变化ΔTr = (2vr/c) Tr通常均可忽略。
当雷达处于脉冲工作状态时, 将发生区别于连续工作状态的特殊问题, 即盲速和频闪效应。
所谓盲速, 是指目标虽然有一定的径向速度vr, 但若其回波信号经过相位检波器后, 输出为一串等幅脉冲, 与固定目标的回波相同, 此时的目标运动速度称为盲速。
而频闪效应则是当脉冲工作状态时, 相位检波器输出端回波脉冲串的包络调制频率Fd, 与目标运动的径向速度vr不再保持正比关系。此时如用包络调制频率测速时将产生测速模糊。
产生盲速和频闪效应的基本原因在于, 脉冲工作状态是对连续发射的取样, 取样后的波形和频谱均将发生变化, 下面将予以讨论。
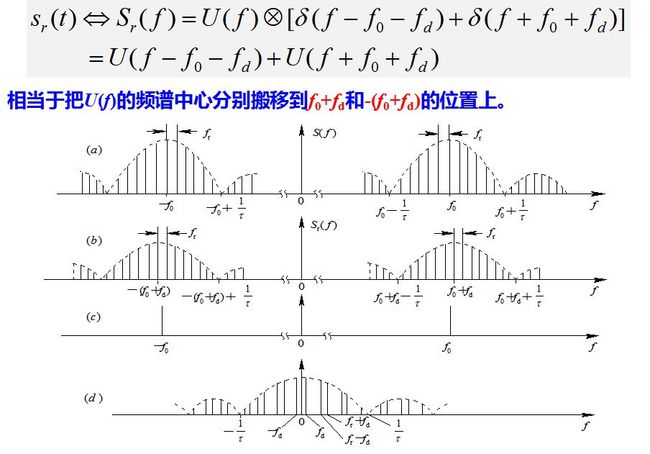
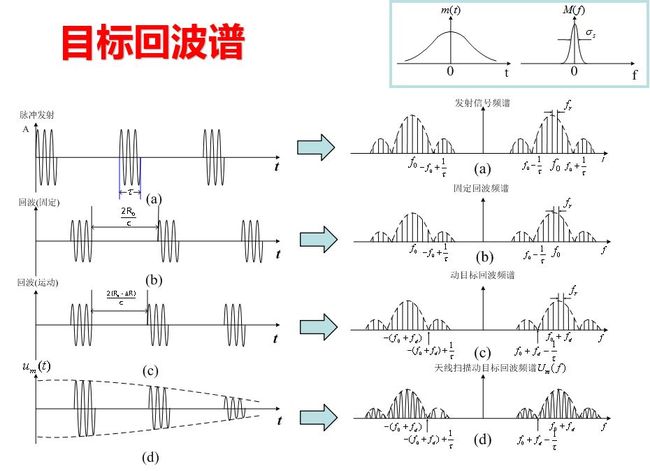
u(t)的频谱U(f)是一串间隔fr = 1/Tr的谱线, 谱线的包络取决于脉冲宽度τ的值。运动目标的回波信号是u(t-tr)和具有多普勒频移的连续振荡相乘, 因而其频谱是两者的卷积,
相位检波器的输入端加有频率为f0的相参电压和回波信号电压, 在其输出端得到两个电压的差频, 如图(d)所示, 其谱线的位置在nfr±fd处, n=0, ±1, ±2, …, 谱线的包络与U(f)相同。
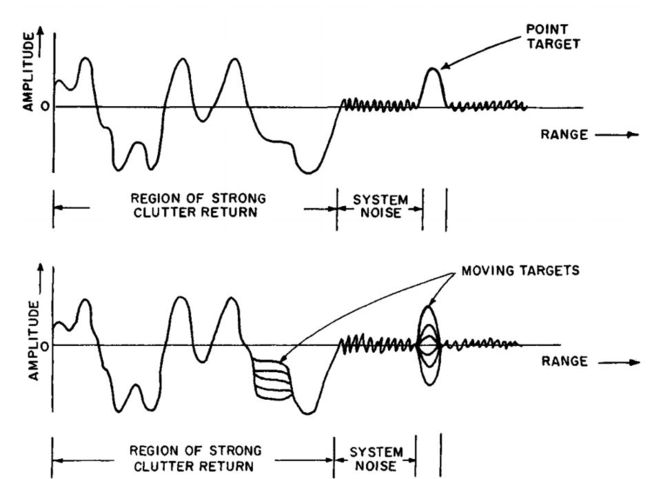
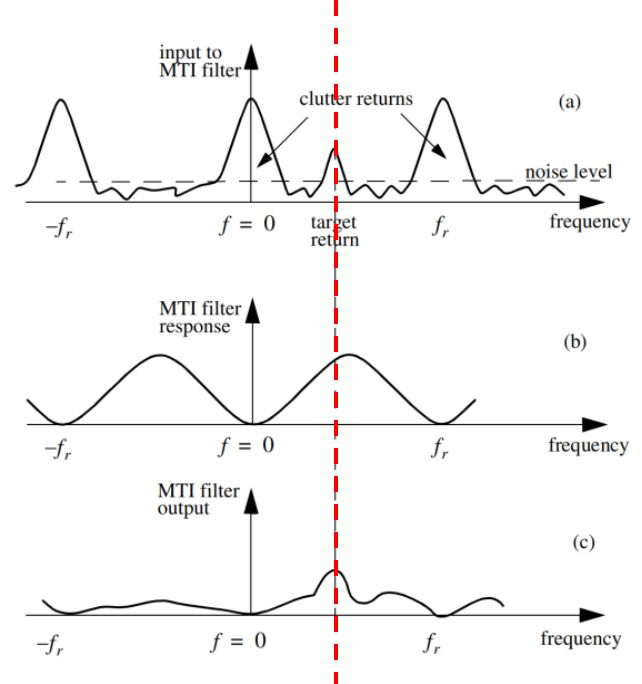
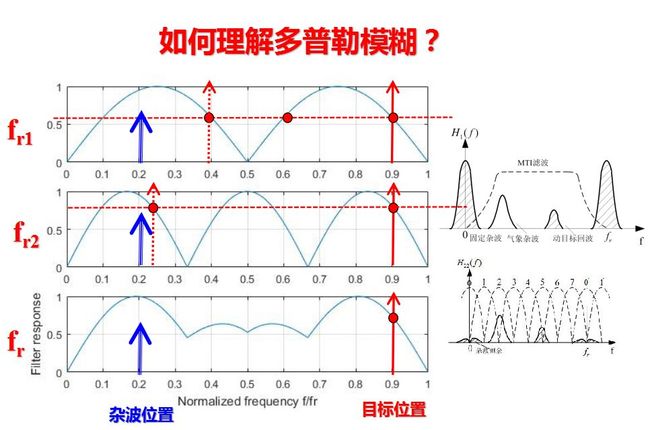
由图的频谱图可以看出脉冲信号产生“盲速”的原因: 固定目标时,fd=0, 其回波的频谱结构与发射信号相同, 是由f0和f0±nfr的谱线所组成。对于运动目标回波, 谱线中心移动fd, 故其频谱由f0+fd、f0+fd±nfr的谱线组成, 经过相位检波器后, 得到fd及nfr±fd的差频, 其波形为多普勒频率fd调幅的一串脉冲。当fd=nfr时, 运动目标回波的谱线由nfr所组成, 频谱结构与固定目标回波的相同, 这时无法区分运动目标与固定目标。
从图的频谱图上也可以分析产生频闪的原因: 当多普勒频率fd超过重复频率fr的一半时, 频率nfr的上边频分量nfr+fd与频率(n+1)fr的下边频分量(n+1)fr-fd在谱线排列的前后位置上交叉。两个不同的多普勒频率fd1和fd2, 只要满足fd1=nfr-fd2, 则二者的谱线位置相同而无法区分。同样, 当fd1=nfr+fd2时, 二者的频谱结构相同也是显而易见的。因此, 在相参脉冲雷达中, 如果要用相位检波器输出脉冲的包络频率来单值地测定目标的速度, 必须满足的条件如上式所示。
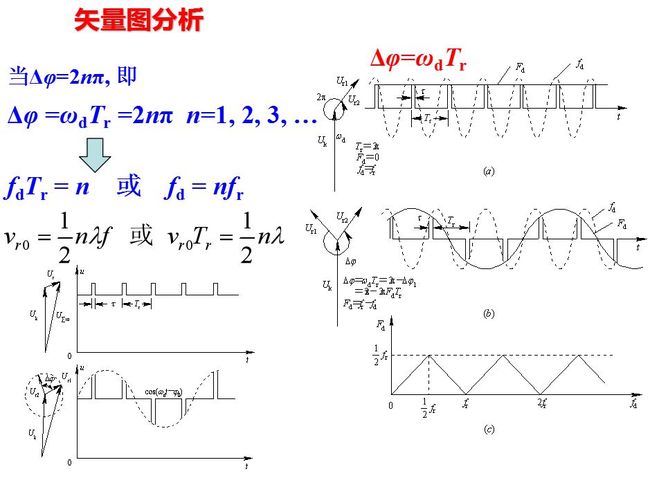
盲速和频闪效应也可以从矢量图和相对应的波形图加以说明。
从矢量图(a)可以看出, 相邻周期运动目标的回波和基准电压之间相位差的变化量为Δφ=ωdTr, 根据Δφ的变化规律即可得到一串振幅变化的视频脉冲。当Δφ=2π时, 虽然目标是运动的, 但相邻周期回波与基准电压间的相对位置不变, 其效果正如目标是不运动的一样, 这就是盲速。可求得盲速与雷达参数的关系。
盲速的出现是因为取样系统的观察是间断而不是连续的。在连续系统中, 多普勒频率总是正比于目标运动的速度而没有模糊。但在脉冲工作时, 相位检波器输出端的回波脉冲包络频率只在多普勒频率较脉冲重复频率低时(fd<1/2fr)才能代表目标的多普勒频率。在盲速时,
即在重复周期内, 目标走过的距离正好是发射高频振荡半波长的整数倍, 由此引起的高频相位差正好是2π的整数倍。
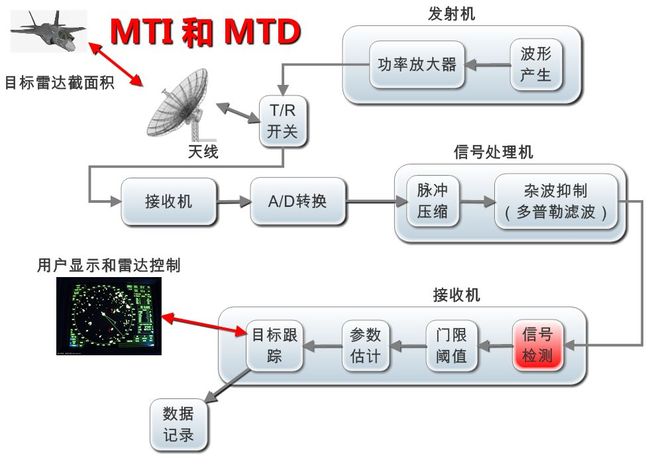
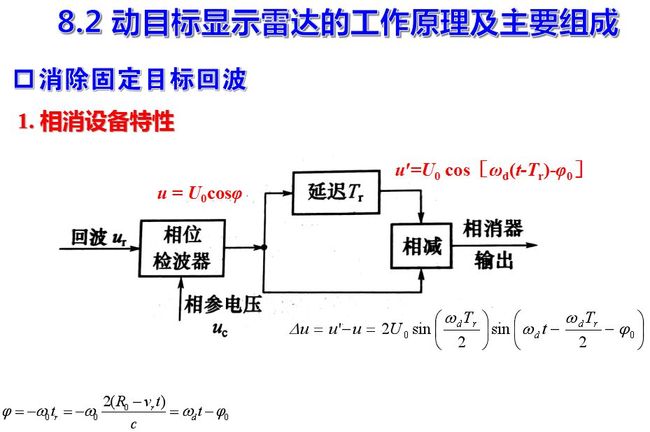
从上节分析可看出, 当脉冲雷达利用多普勒效应来鉴别运动目标回波和固定目标回波时, 与普通脉冲雷达的差别是必须在相位检波器的输入端加上基准电压(或称相参电压), 该电压应和发射信号频率相参并保存发射信号的初相, 且在整个接收信号期间连续存在。工程上,基准电压的频率常适在中频。这个基准电压是相位检波器的相位基准, 各种回波信号均与基准电压比较相位。从相位检波器输出的视频脉冲, 有固定目标的等幅脉冲串和运动目标的调幅脉冲串。通常在送到终端(显示器或数据处理系统)去之前要将固定杂波消去, 故要采用相消设备或杂波滤波器, 滤去杂波干扰而保存运动目标信息。
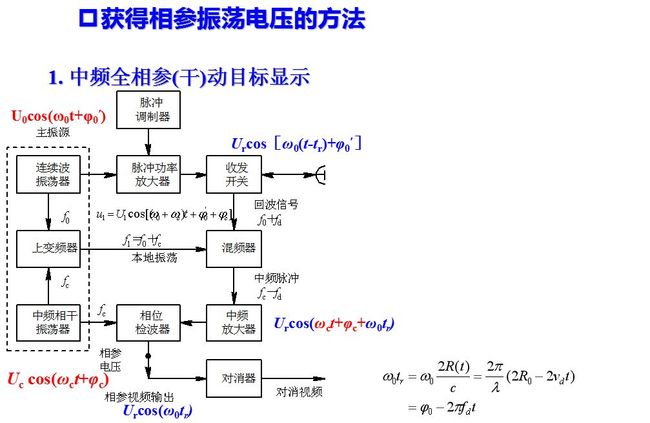
当雷达发射机采用主振放大器时, 每次发射脉冲的初相由连续振荡的主振源控制, 发射信号是全相参的, 即发射高频脉冲、 本振电压、相参电压之间均有确定的相位关系。相位检波通常是在中频上进行的, 因为在超外差接收机中, 信号的放大主要依靠中频放大器。在中频进行相位检波, 仍能保持和高频相位检波相同的相位关系。
如图所示,主振源连续振荡的信号为U0cos(ω0t+φ0′), 它控制发射信号的频率和相位。中频相参振荡器的输出为Uc cos(ωct+φc)。本振信号取主振源连续振荡信号和相参源的和频, 即
回波信号为Urcos[ω0(t-tr)+φ0′], 对于固定目标, tr为常数。而对于运动目标,tr在每个重复周期均发生变化。回波信号与本振混频后取出中频信号: 对于运动目标的回波, 二者相位差按多普勒频率变化。
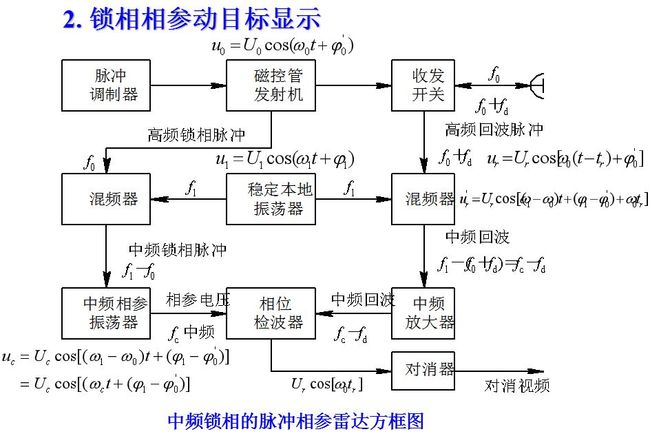
当雷达发射机采用自激振荡器(如磁控管振荡器)时, 它的每一发射脉冲高频起始相位是随机的。因此,为了得到与发射脉冲起始相位保持严格关系的基准电压, 应该采用锁相的办法, 也就是使振荡电压的起始相位受外加电压相位的控制。原则上有两种锁相的办法: 一种是将发射机输出的高频电压加到相参振荡器去锁相; 另一种是将连续振荡的相参电压加到发射机振荡器去, 以控制发射脉冲的起始相位。后一种方法要求较大的控制功率, 因而在实际中用得较少。直接用发射机输出在高频进行锁相存在着实际困难, 因为容易实现锁相和高频率稳定度两个要求对锁相振荡器的实现是互相矛盾的。如果允许的频偏量Δf相同(Δf的值影响动目标显示的工作质量), 则锁相相参振荡器工作在中频时对频率稳定度Δf/fc的要求将明显降低。加之超外差接收通常在中频进行主要放大, 并将中频信号送到相位检波器, 因此, 典型动目标显示的相参振荡器均工作于中频, 在中频上实现锁相。其组成方框图如图所示。锁相电压直接由发射机取出, 避免了收发开关可能带来的干扰, 以保证锁相质量。高频锁相电压与回波信号用同一本振电压混频, 然后将混频所得的中频锁相电压加到相参振荡器输入端。用这个锁相电压锁定的中频相参振荡器电压可以作为相位检波器的基准电压。发射信号和本振信号的随机初相在比较相位时均可以消去。
在相位检波器中, 回波信号ur′与基准电压比较相位时, 初相φl-φ0′可以消去, 两者的相位差只决定于ω0tr。当目标运动时, 相邻重复周期的相位差按多普勒频率变化。
式中,φ为回波与基准电压之间的相位差, 回波信号按重复周期Tr出现, 将回波信号延迟一周期后, 其包络为 上式。
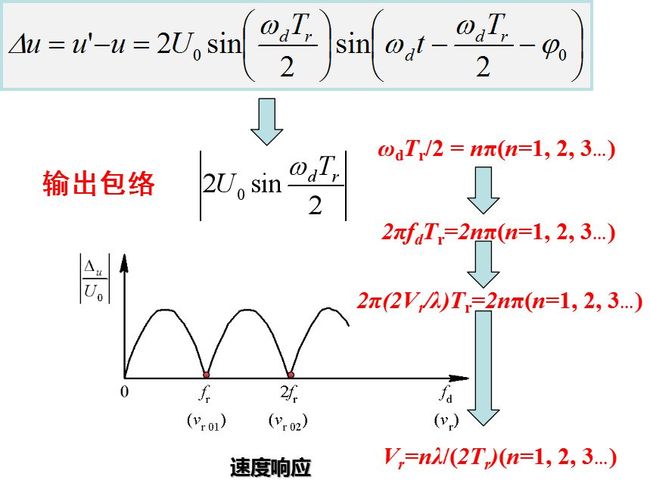
输出包络为一多普勒频率的正弦信号, 其振幅为上式所示。
也是多普勒频率的函数。当ωdTr/2 = nπ(n=1, 2, 3…)时, 输出振幅为零。这时的目标速度正相当于盲速。此时,运动目标回波在相位检波器的输出端与固定目标回波相同, 因而经相消设备后输出为零, 如图所示。
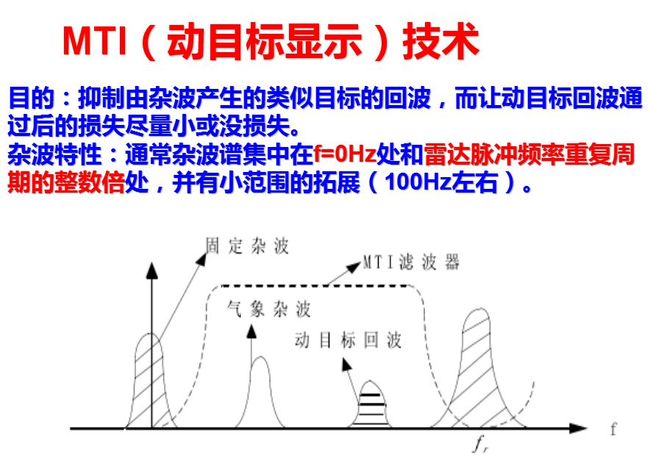
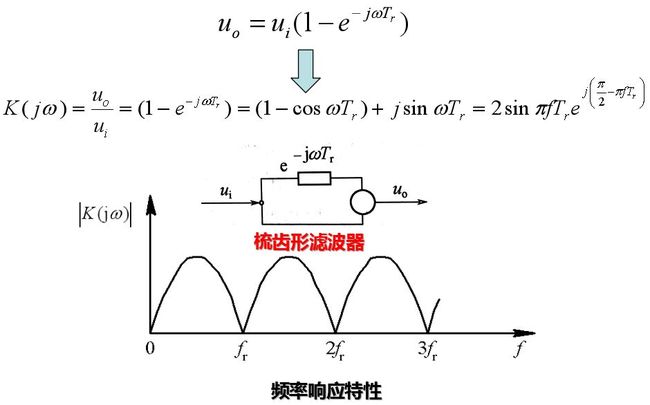
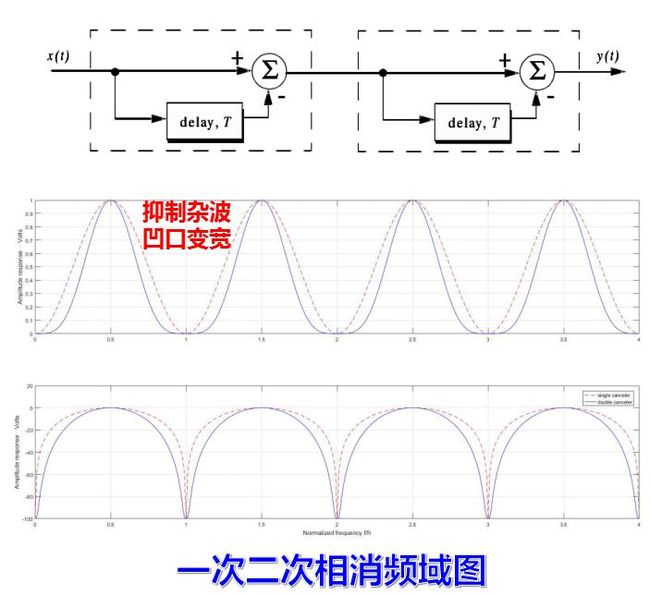
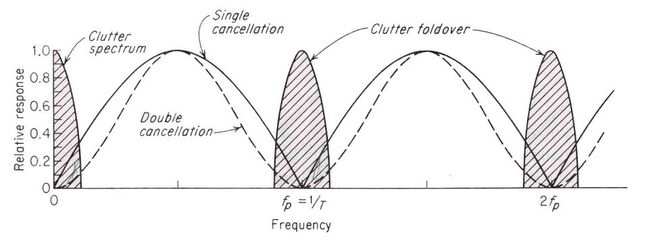
相消设备也可以从频率域滤波器的观点来说明, 而且为了得到更好的杂波抑制性能, 常从频率域设计较好的滤波器来达到。下面求出相消设备的频率响应特性。相消设备等效于一个梳齿形滤波器, 其频率特性在f=nfr各点均为零。固定目标频谱的特点是, 谱线位于nfr点上, 因而在理想情况下, 通过相消器这样的梳齿滤波器后输出为零。当目标的多普勒频率为重复频率整数倍时, 其频谱结构也有相同的特点, 故通过上述梳状滤波器后无输出。
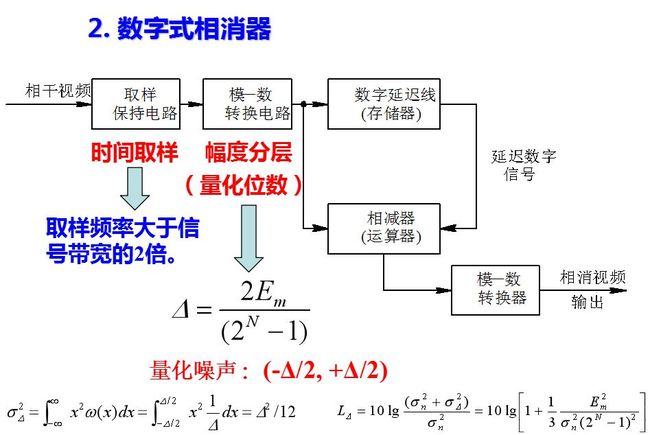
数字式相消器的简单组成如图所示。作为模拟和数字信号的接口, 首先要把从相位检波器输出的模拟信号变为数字信号。模拟信号变为数字信号要经过时间取样和幅度分层两步。以时钟脉冲控制取样保持电路对输入相参视频信号取样, 被时间量化的取样保持信号送到模数转换电路(A/D变换器)进行幅度分层, 转为数字信号输出。数字信号的迟延可用存储器完成, 将数字信号按取样顺序写入存储器内, 当下一个重复周期的数字信号到来时, 由存储器中读出同一距离单元的信号进行相减运算, 在输出端得到跨周期相消的数字信号。这个数字信号可以很方便地用来作其它数字处理(例如积累、恒虚警等), 如果需要模拟信号作显示, 则可将数字信号经过数模转换器, 变为模拟信号输出。模拟信号转换为数字信号时, 取样间隔和量化位数这两个参数的选择必须慎重。取样定理证明, 如果取样信号要保留原信号的全部信息, 取样间隔ΔT应小于信号有效带宽倒数的一半, 即取样频率1/ΔT大于信号带宽的2倍。
每一个雷达杂波的回波为许多反射单元的回波矢量和, 其功率谱与单个发射脉冲谱的形状相类似。单个目标雷达回波的有效带宽通常以其脉冲宽度的倒数表示,所以取样间隔应小于脉冲宽度的一半, 即在一个脉冲宽度以内取样两次以上。
取样次数增多虽可提高取样信号的质量, 但实现起来所用设备量将增加。在雷达信号的量化过程中, 有时在一个脉冲宽度内只取样一次, 这样可以简化设备, 它所引起的信杂比损耗约为1.5 dB。
量化位数(模数转换位数)的选取, 主要取决于量化噪声的影响。模数转换首先将模拟信号量化分层。如数字位数为N, 则将输入动态范围(设从-Em到+Em)分成2N-1层, 幅度量化间隔为
将幅度连续变化的取样保持信号量化为离散的分层数字信号, 二者之间当然会有差别, 这个差别称为量化噪声。分层时, 连续的取样保持信号和量化的标准电平相比较, 以二分层的中线为界: 超过中线的归于上层, 低于中线的归于下层。这样一来, 量化噪声限制在(-Δ/2, +Δ/2)的区间内, 且在一般情况下, 在该区间内量化噪声分布的概率密度为均匀分布
输入的模拟信号包括目标回波、杂波和噪声, 经过幅度分层量化以后, 将增加一部分量化噪声。量化后总噪声的均方值σ2可以认为是原噪声均方值σ2n和量化噪声均方值σ2Δ之和, 则由于量化引起的信噪比损失(量化损耗)为上式所示。
这时fd0=nfr或vr0=(n/2) λfr, n=1时为第一盲速, 表示在重复周期Tr内目标所走过的距离为半个波长。由于处于“盲速”上的运动目标, 其回波的频谱结构和固定杂波相同, 经过对消器将被消除。因此, 动目标显示雷达在检测“盲速”范围内的运动目标时, 将会产生丢失或极大降低其检测能力(这时依靠复杂目标反射谱中的其他频率分量)。如果要可靠地发现目标, 应保证第一盲速大于可能出现的目标最大速度。
但在均匀重复周期时, 盲速和工作波长λ以及重复频率fr的关系是确定的, 这两个参数的选择还受到其他因素的限制。以3 cm雷达为例, 如果最大测距范围为30km, 则其重复频率fr应小于5kHz, 由这个参数决定的第一盲速值vr01 = (λ/2) fr=75m/s, 这个速度远低于目前超音速目标的速度, 也就是说, 如果不采取措施, 在目标运动的速度范围内, 将多次碰到各个盲速点而发生丢失目标的危险。事实上, 最大不模糊距离和重复频率fr的关系为
当工作波长λ选定后, 两者的乘积为一常数, 不能任意选定。通常在地面雷达中, 常选择其重复频率fr使之满足最大作用距离的要求, 保证测距无模糊, 而另外设法解决盲速问题。
解决盲速问题在原理上并不困难, 因为在产生“盲速”时, 满足vrTr1 = n (λ/2), 如果这时将重复周期略为改变而成为Tr2, 则vrTr2≠ n (λ/2), 不再满足“盲速”的条件, 动目标显示雷达就能检测到这一类目标。因此, 当雷达工作时, 采用两个以上不同重复频率交替工作(称为参差重复频率), 就可以改善“盲速”对动目标显示雷达的影响。
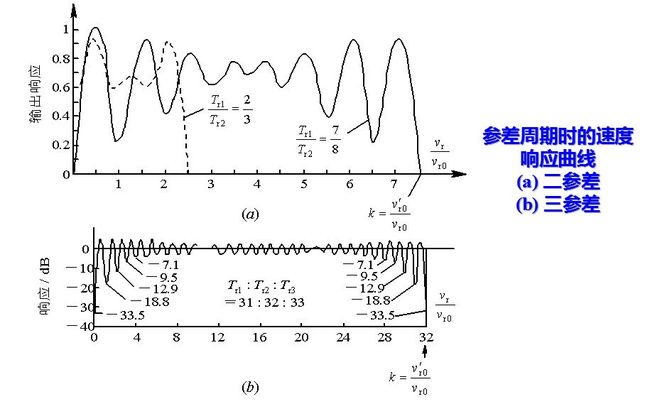
在实际工作中, 不仅要求第一等效盲速值要尽可能覆盖目标可能出现的速度范围, 而且要求在该速度范围内响应曲线比较平坦。这两个要求实现起来常有矛盾, 需要选择合适的参差数和最佳的参差比来解决。以两个重复频率参差的情况来说, 盲速提高倍数愈多, 则合成曲线愈不平坦, 特别是第一凹点深度愈大, 这是不希望的。改进的办法是采用三个以上重复频率的参差及好的参差比来得到较好的速度响应特性。图画出了几种不同情况下的速度响应, 横坐标为归一化的速度响应vr/vr0, k表示合成盲速比原盲速增大的倍数, 参差比不同时, k的值是不同的。
在(a)图中, 当Tr1/Tr2 = 2/3时, 盲速提高为原来的2.5倍, 而当Tr1/Tr2 =7/8时, 盲速提高为原来的7.5倍, 但在原来第一盲速处输出较小, 速度响应不平坦。图8.12(b)是三参差周期, 其比值为31∶32∶33的速度响应。可以看出,三参差可较二参差获得较平坦的响应曲线。如果选用合适参差比的四参差时, 其速度响应将更为平坦。
滤波器组成原理图如图所示。滤波器对N-1个重复周期的信号进行滤波处理, 在参差重复周期时, ti-ti-1=Ti(i=1, 2, …,N-1)各不相等, 速度响应主要取决于参差比值的选择, 与权值wi也有一些关系。在等重复周期条件下, 多级对消器串接时, 其权值服从二项式。
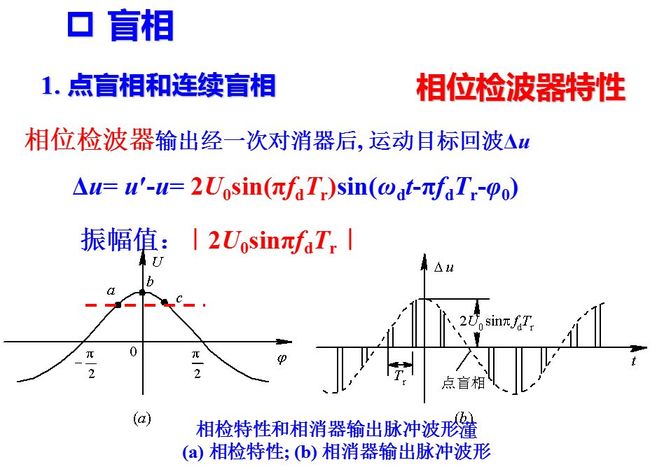
输出的振幅值大小为|2U0sinπfdTr|, 与多普勒频率有关, 其输出的振幅受多普勒频率调制。在某些点上, 输出幅度为零, 这些点称为盲相, 它由相位检波器的特性(见图(a))决定。从相检特性上看, 如果相邻两个回波脉冲的相位相当于相检特性的a、c二点, 其相位差虽不同, 但却是一对相检器输出相等的工作点, 因此经过相消器后, 其输出为零而出现点盲相。
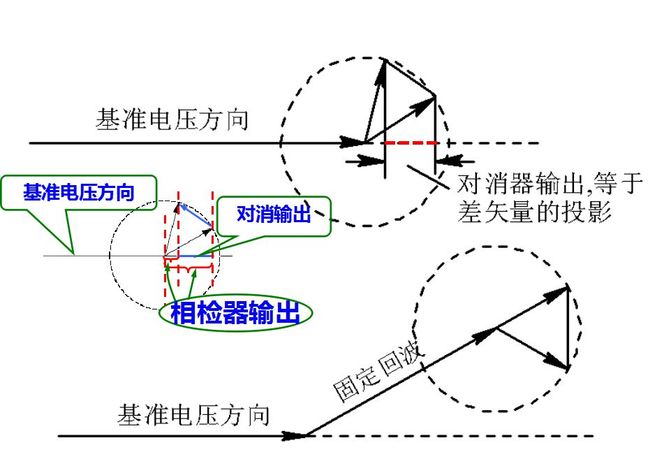
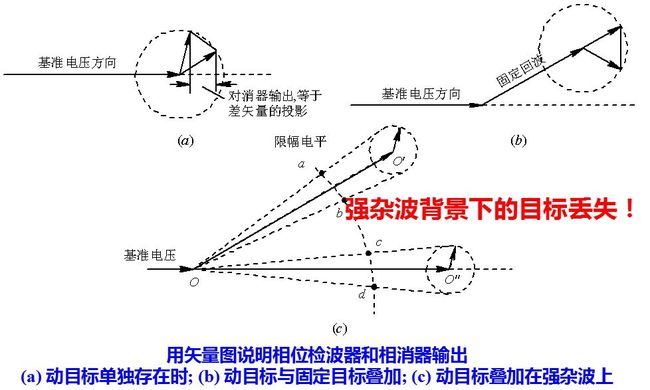
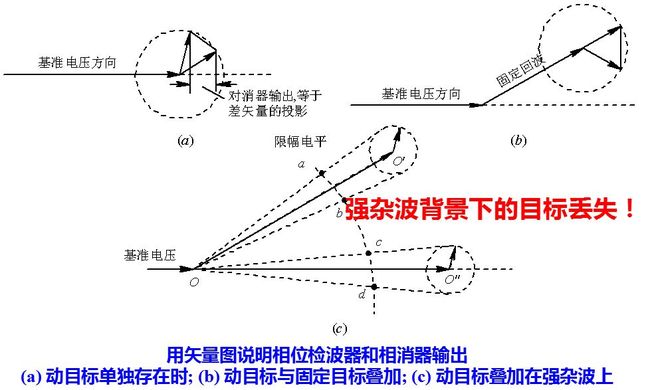
(a)匀速运动的目标回波信号用围绕基准电压匀速旋转的一个矢量来表示,旋转的速度等于其多普勒频率,相位检波器的输出为该矢量沿基站电压方向的投影。一次对消器的输出为相邻重复周期差矢量在基准电压轴方向的投影。当投影长度为零时,出现盲相。当运动目标回波叠加到固定杂波时,一般情况也会出现盲相。
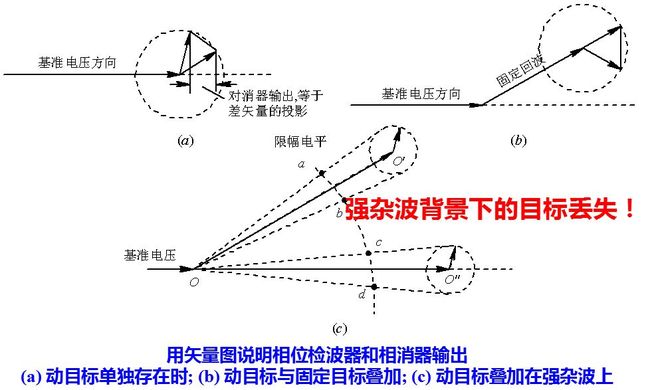
如果目标回波叠加到很强的杂波上,可能产生连续盲相。
由于接收机的限幅租用使动目标和固定杂波的合成矢量变成了端点在限幅电平的一小段圆弧上来回摆动的矢量。,杂波相对基准信号的相位不同时,所占弧的位置不一样,如果碰到如图所示的固定杂波相位,其合成矢量经过限幅以后端点在cd之间摆动,差不多所有情况下差矢量都垂直于基准轴,相消器几乎没有输出,这种情况称为连续盲相,即对于一定相位的固定杂波,叠加在他上面的运动目标回波将连续丢失。
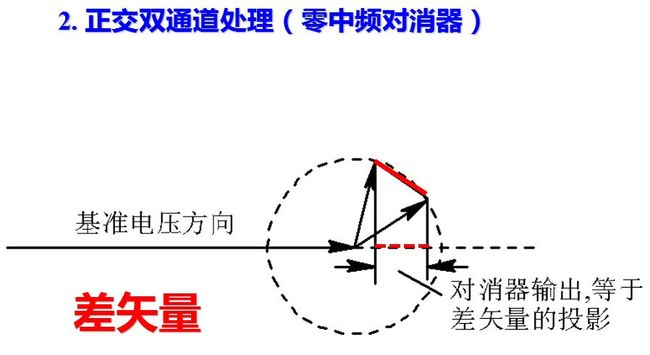
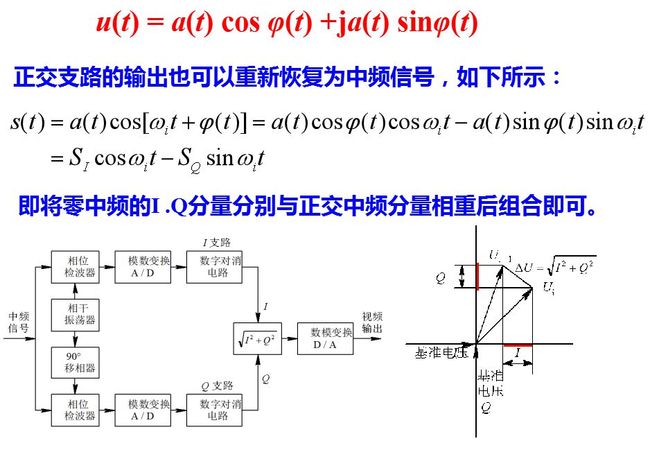
从相位检波器的讨论中可看出, 相位检波器的输出是回波矢量在基准电压方向的投影, 而一次对消器的输出又相当于相邻重复周期信号差矢量在该方向的投影。当差矢量的方向与基准电压方向垂直时, 则输出为零, 这时就是盲相。如果能在信号处理中, 直接取出反射回波的差矢量, 则避免了盲相和回波振幅的多普勒调制。在检波前直接用中频对消, 可以取出反射回波的差矢量。
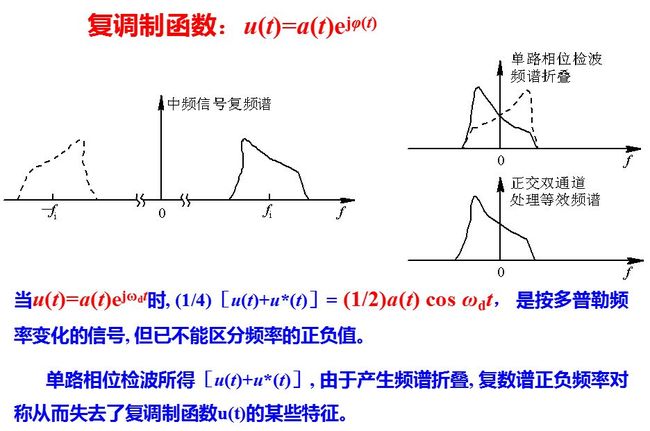
式中,u(t)=a(t)ejφ(t),称为复调制函数, 它包含了信号s(t)中的全部信息, 即振幅调制和相位调制函数。以φ(t)=ωdt为例来看, 复调制函数u(t)=a(t)ejωdt表示中频信号附加的多普勒频率为正值, 可以从复调制函数的实部和虚部的相互关系中, 判断频率的正负值。
相位检波器是将中频信号s(t)与相参电压差拍比较, 它的工作原理与混频相同, 相参电压类似于混频时的“本振”电压。
通常都选取相参振荡的频率和信号中频相同, 因此,相位检波器输出的差拍为零, 称之为“零中频”或“基频”信号。
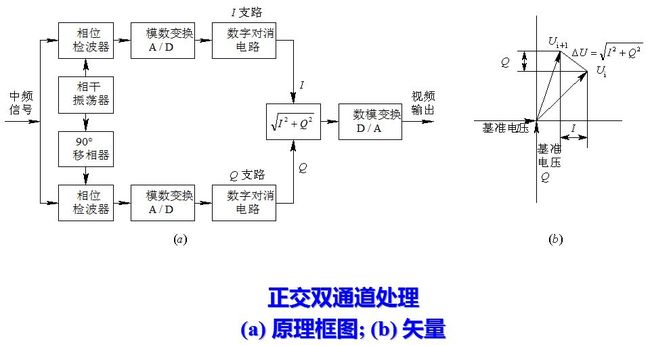
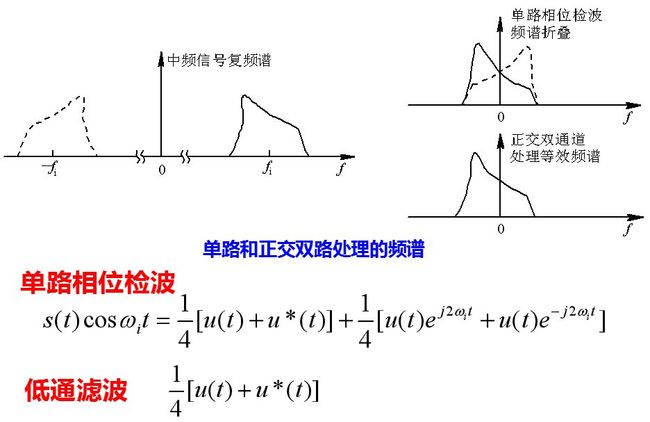
相位检波器虽然可以保留中频信号的相位信息, 但是只用单路相位检波器时, 将原中频信号在正频率轴与负频率轴上的频谱, 全部移到零频率的位置上, 从而产生了频谱折叠, 如图8.4和图8.19所示。这时已不能保留复调制函数u(t)的全部信息。单路相位检波器完成的作用是将信号s(t)与基准电压 cosωit相乘,。
这就要求正交双通道处理, 一支路和基准电压cosωit 进行相位检波, 称为同相支路I; 另一路和基准电压sinωit进行相位检波, 得到正交支路Q, sinωit 由cosωit移相90°得来。故输出值分别为a(t)cosφ(t) 和a(t) sin φ(t)。如果要取振幅函数a(t)(中频矢量值), 则同相和正交支路取平方和再开方; 如果要判断相位调制函数的正负值, 则需比较I、Q两支路的相对值来判断。
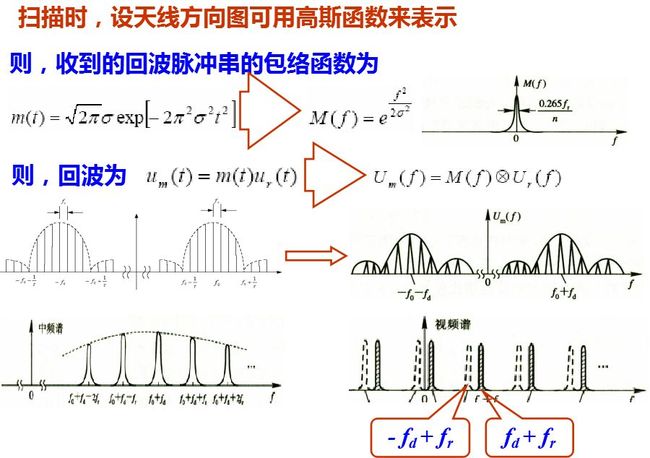
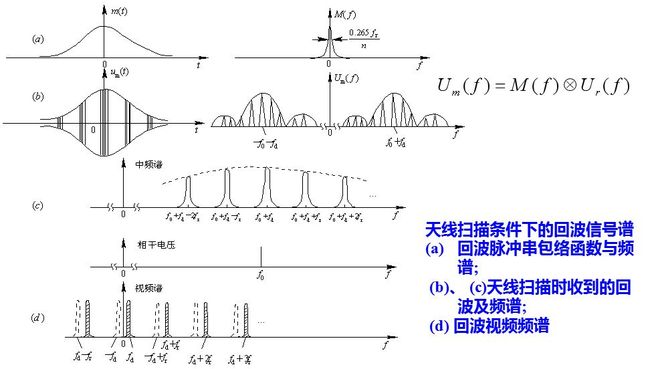
雷达工作时, 天线总是以各种方式进行扫描。这时收到的回波脉冲为有限数, 且其振幅受天线方向图调制。设天线方向图可用高斯函数来表示, 则收到回波脉冲串的包络函数可写为 m(t)。
式中,σ是和天线波瓣宽度及扫描速度均有关的参数。σ减小, 表示观察的时间增加。天线扫描时所收到的回波信号, 可以用m(t)和无限脉冲串ur(t)的乘积表示,ur(t)为天线不扫描时的回波脉冲串。
即无限回波脉冲串频谱Ur(f)的每一根谱线均按M(f)的形状展宽, 如图(b)、(c)所示。谱线展宽的程度反比于天线波束照射目标的时间Tθ 。
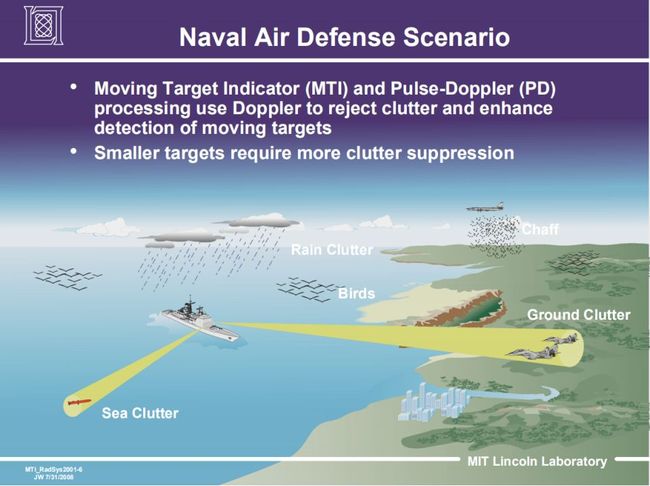
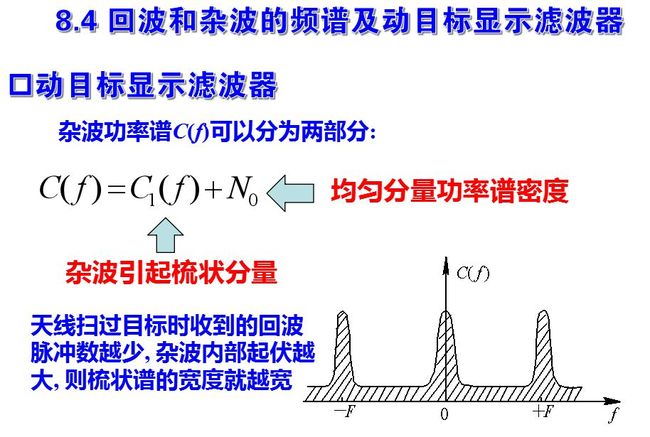
雷达工作时可能碰到的杂波, 包括地物、海浪、云雨及敌人施放的金属箔等。除了孤立的建筑物等可认为是固定点目标外, 大多数杂波均属于分布杂波且包含内部运动。在上面讨论信号频谱时已包括对固定点杂波的频谱的讨论。其中,σs= 0.265fr/n, n为在单程天线方向图三分贝宽度内的脉冲数。设Tθ为天线照射目标的等效时间,则n=Tθfr, 即σs= 0265/Tθ, 亦即σs与目标照射时间成反比, 大多数分布杂波的回波性质比较复杂。在雷达的分辨单元内, 雷达所收到的回波是大量独立单元反射的合成, 它们之间具有相对的运动, 其合成回波具有随机的性质。且由于杂波内部的运动, 各反射单元所反射的多普勒频率值不同, 这就引起回波谱的展宽。
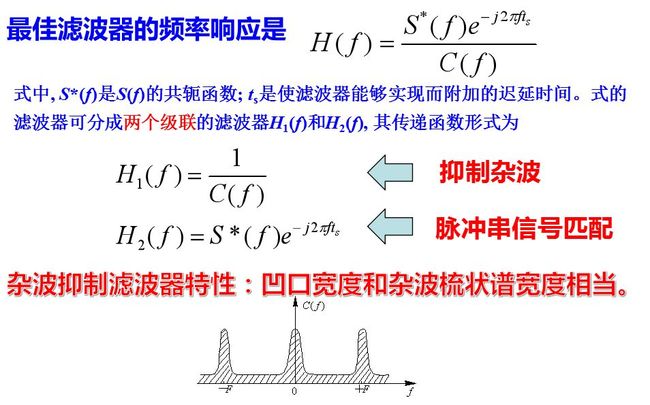
由于杂波谱线的展宽, 简单的一次对消滤波器将不能很好地滤去杂波, 需要进一步改进滤波器的特性。特别是杂波具有多普勒频移时, 滤波器的凹口还应对准杂波谱的平均多普勒频率位置才能收到预期结果。
杂波谱的展宽将明显地影响动目标显示系统的质量, 因为滤波器不仅要滤去杂波谱, 还应保证运动目标回波在尽可能大的速度范围内均有大的输出, 因而滤波器的凹口又不能做得很宽。
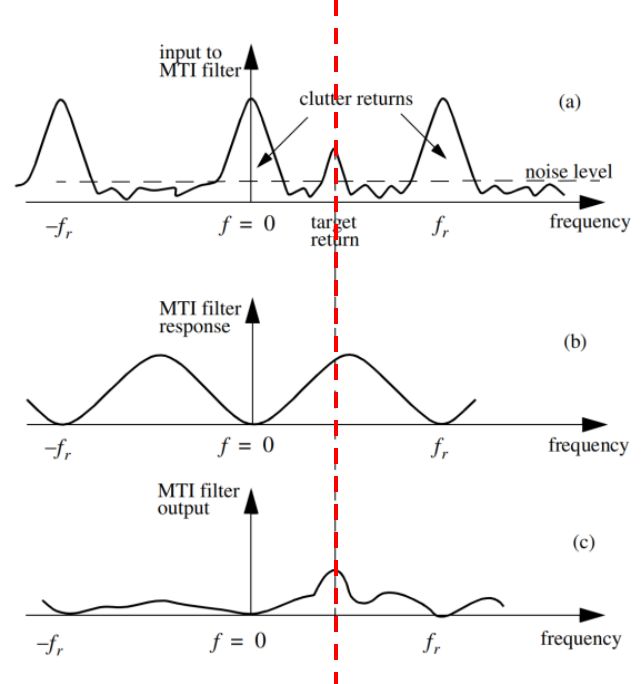
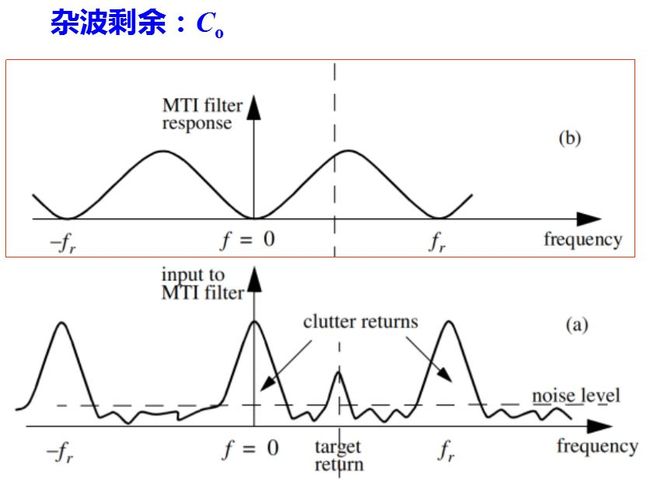
其中, N0为均匀分量的功率谱密度, 它取决于系统的稳定性, 稳定性越高, N0越小。C1(f)是由杂波特性(包括天线扫描和杂波内部起伏)决定的梳状分量, 天线扫过目标时收到的回波脉冲数越少, 杂波内部起伏越大, 则梳状谱的宽度就越宽。
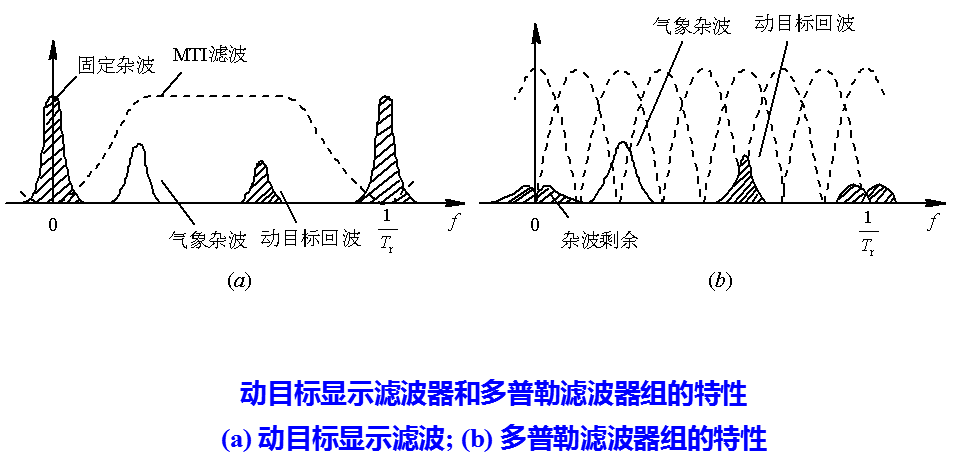
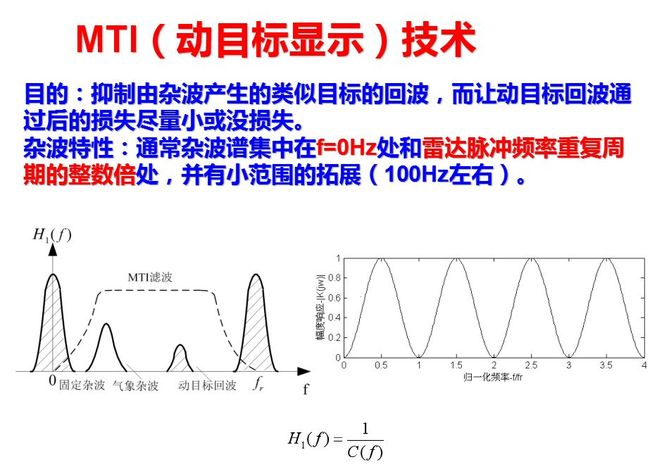
动目标显示器利用运动目标和杂波在频谱上的区别,可有效的抑制杂波而提取信号。
根据最佳滤波理论, 当杂波功率谱C(f)和信号频谱S(f)已知时, 最佳滤波器的频率响应是H(f)粗略地认为, 其中H1(f)用来抑制杂波, H2(f)用来对脉冲串信号匹配。
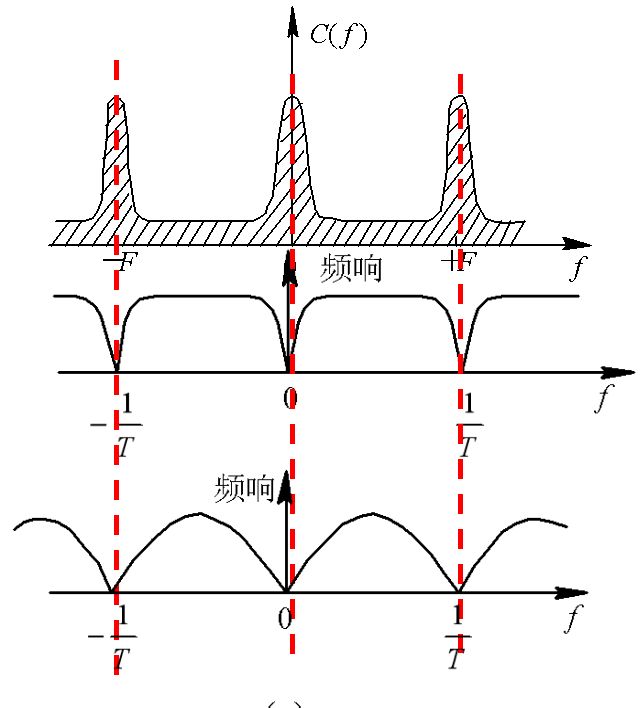
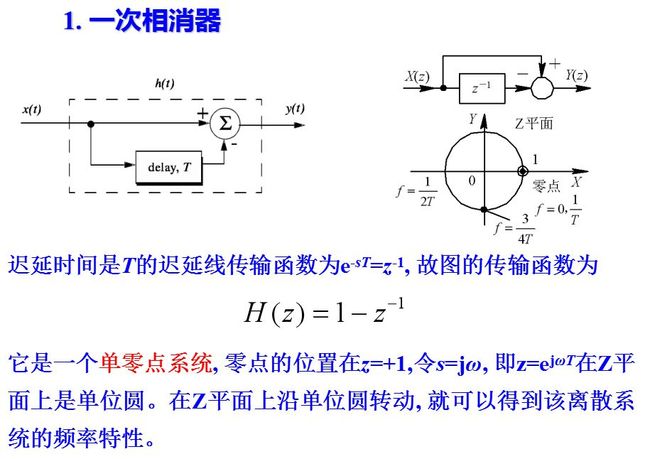
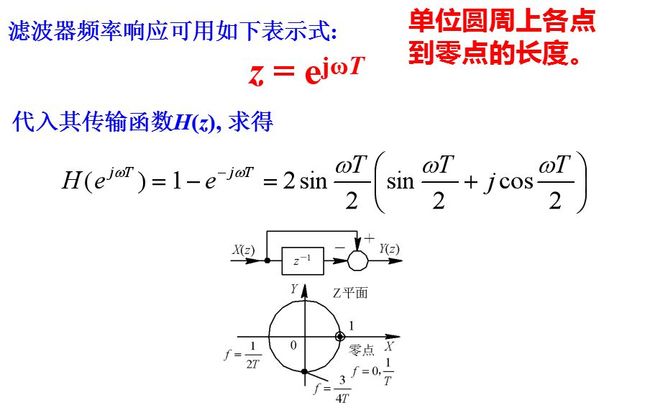
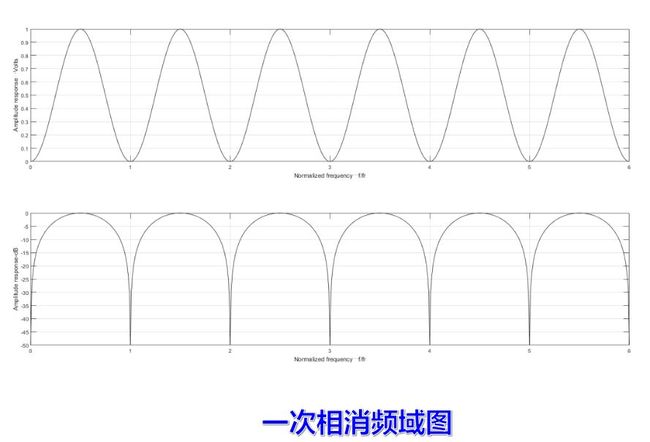
对于上述一次对消器, 其频率特性即为对应于单位圆周上各点到零点(z=+1)的长度。根据z=ejωT的关系可以看出, 当频率f从零变到1/T时, 幅角ωT从零变化到2π, 沿单位圆转了一周。当频率从1/T变化到2/T时, 幅角ωT沿单位圆重复转一周。由此可见, 时间离散系统的频率响应是以1/T为周期的重复函数。
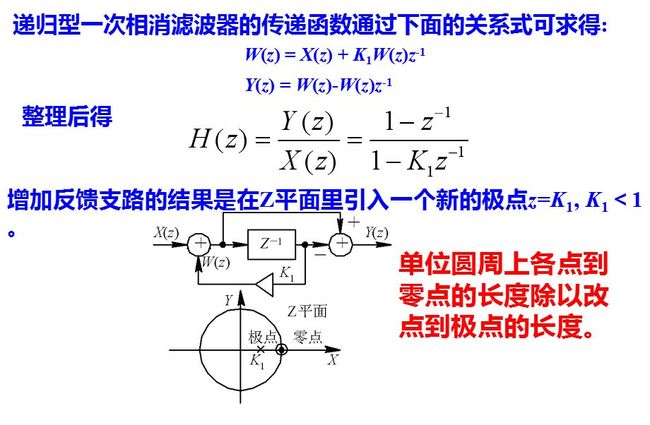
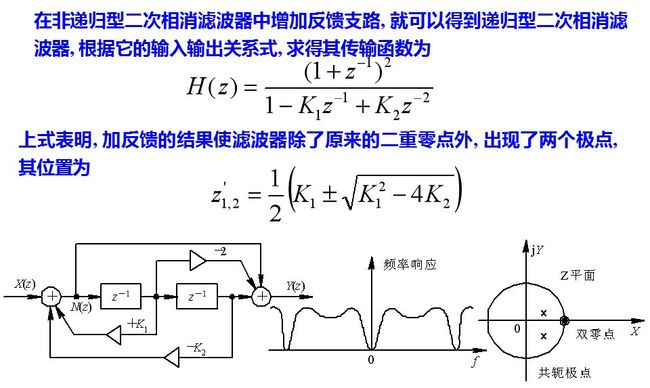
如果将一次相消滤波器加一条反馈支路, 就可以改变滤波器的频率特性。通常把有反馈支路的滤波器称为递归型滤波器, 相应地, 把无反馈支路的滤波器称为非递归型。
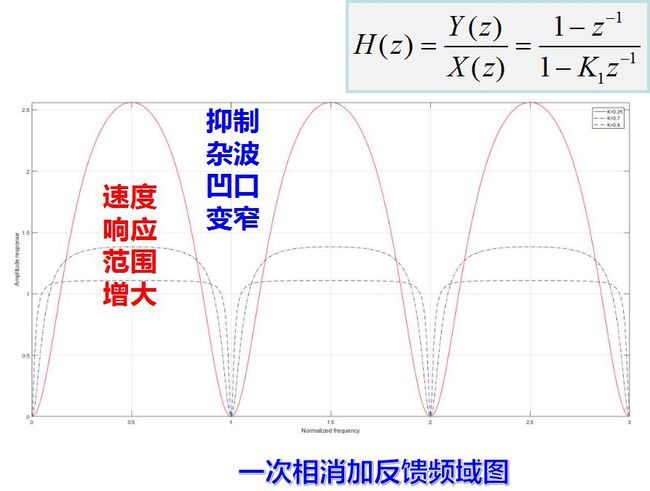
滤波器的频率响应为单位圆上的点到零点的长度被该点到极点的长度去除。从图可以看出, 如果K1接近于1, 则极点和零点十分接近, 在单位圆上的各点(相当于不同频率), 除了靠近零点的一小段外, 上述两个长度近似相等, 二者相除近似为常数, 即频率响应很平坦。在零点附近的一小段, 靠极点也很近, 因此两个长度相除后较之只有零点时的频率响应值加大, 而使滤波器抑制杂波的凹口变窄。K1越接近于1, 滤波器频率响应的平坦范围就越宽, 但抑制杂波的凹口也越窄。在简单的动目标显示雷达(MTI)中, 利用这种方法来扩大速度响应范围。
当K21<4K2时, 它们是一对共轭极点。这对极点的作用是使在它附近的频率点上所相应的频率响应值得到提高, 这样, 整个通频带范围内可以有较为平坦的频率响应曲线。改变极点的位置, 可使频率响应得到变化。滤波器频率响应的表示式可将z=e jωTr代入H(z)中得到。
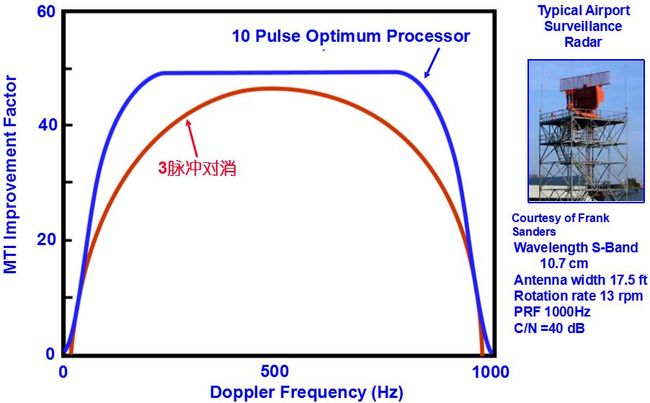
式中,Si和So为在目标所有可能的径向速度上取平均的信号功率;G为系统对信号的平均功率增益。之所以要取平均, 是因系统对不同的多普勒频率响应不同, 而目标的多普勒频率在很大范围内分布之故。
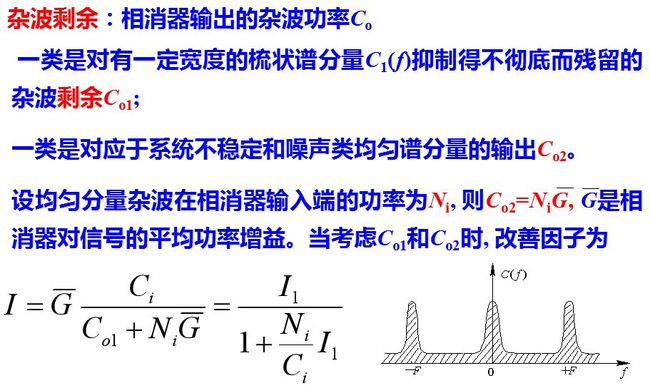
相消器输出的杂波功率Co习惯上称为杂波剩余, 它由多种因素形成。从性质上可分为两类: 一类是对有一定宽度的梳状谱分量C1(f)抑制得不彻底而残留的杂波剩余Co1; 另一类是对应于系统不稳定和噪声类均匀谱分量的输出Co2。设均匀分量杂波在相消器输入端的功率为Ni, 则Co2=NiG, G是相消器对信号的平均功率增益。当考虑Co1和Co2时, 改善因子为
如果目标回波叠加到很强的杂波上,可能产生连续盲相。
由于接收机的限幅租用使动目标和固定杂波的合成矢量变成了端点在限幅电平的一小段圆弧上来回摆动的矢量。,杂波相对基准信号的相位不同时,所占弧的位置不一样,如果碰到如图所示的固定杂波相位,其合成矢量经过限幅以后端点在cd之间摆动,差不多所有情况下差矢量都垂直于基准轴,相消器几乎没有输出,这种情况称为连续盲相,即对于一定相位的固定杂波,叠加在他上面的运动目标回波将连续丢失。
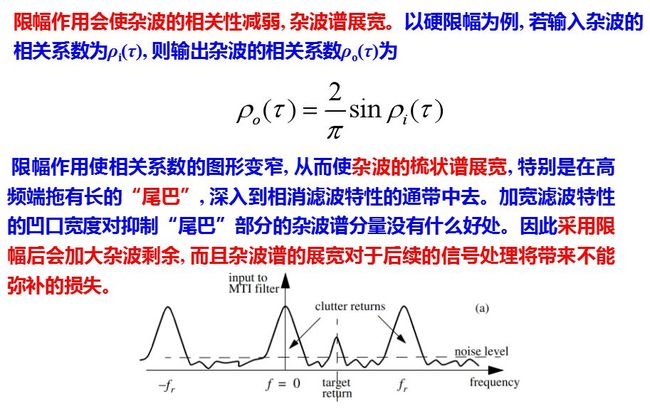
但是中放限幅也会带来一些不利的因素: 限幅会使强杂波背景上的运动目标信号受到损失, 波形产生失真, 并妨碍后续的信号处理, 个别情况还可能产生连续盲相。不仅如此, 限幅作用会使杂波的相关性减弱, 杂波谱展宽。以硬限幅为例, 若输入杂波的相关系数为ρi(τ), 则输出杂波的相关系数ρo(τ)为 上式所示。
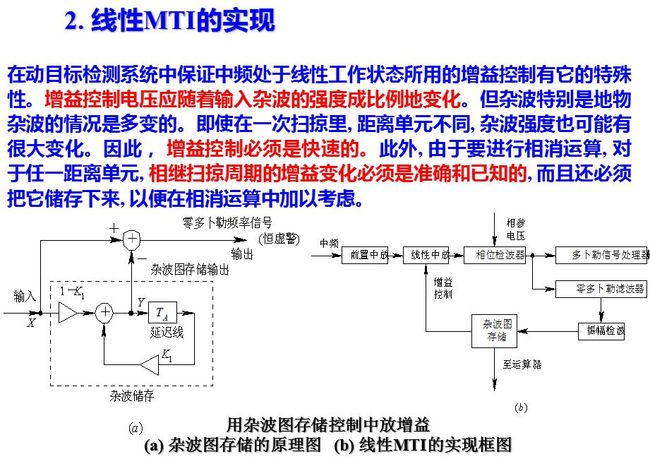
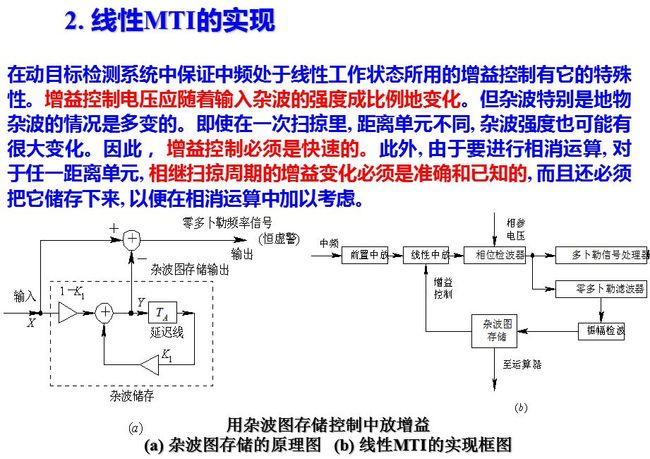
由于雷达收到的杂波回波强度很大, 为了避免产生限幅, 就应当采用动态范围达60dB或80 ~ 90 dB的高频和中频放大器。一般的高频放大器, 特别是中频放大器不可能有这样大的动态范围, 只有借助于增益控制。
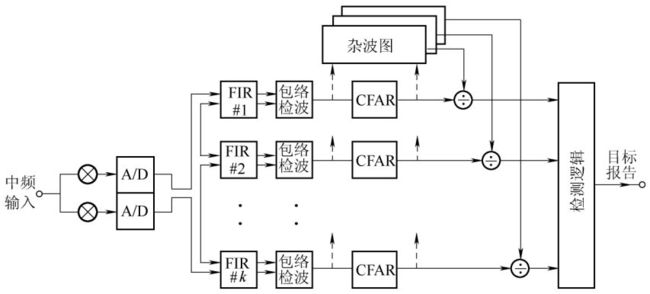
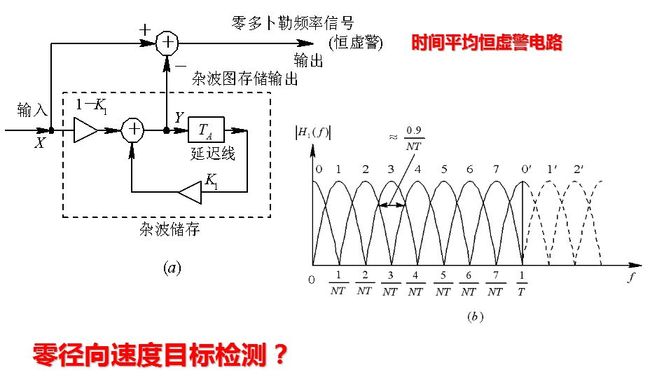
地杂波图存储应该随着实际情况及时更新, 因为要用“时间单元平均”的杂波图作为检测切向飞行目标之用。所谓“时间单元”平均,就是以一个天线扫描周期作为一个单元。每个空间单元里储存的应是多次天线扫描所得杂波的平均值估值。为了不使设备过于复杂, 不宜采用多次扫描存储的滑窗式积累, 而应采用单回路反馈积累的办法。
杂波图存储的输出如果只用来控制中放增益, 则其量化的数字位可以较少。如果该杂波图同时用作零多普勒信号的检测, 则为了得到好的检测性能, 存储的数码应有足够的位数, 典型值为8到12 bit, 以便同时能容纳输入端信号的全部动态范围。可见杂波图的存储量是很大的, 除了存储地杂波的信息外, 在精巧的信号处理系统中还可能有存储其它信息的“地图”(如运动杂波、速度信息等), 其单元尺寸以及性能参数将根据具体要求而定, 由于超大规模集成电路的迅猛发展, 实现大容量的存储及相应的运算在技术上是不困难的。
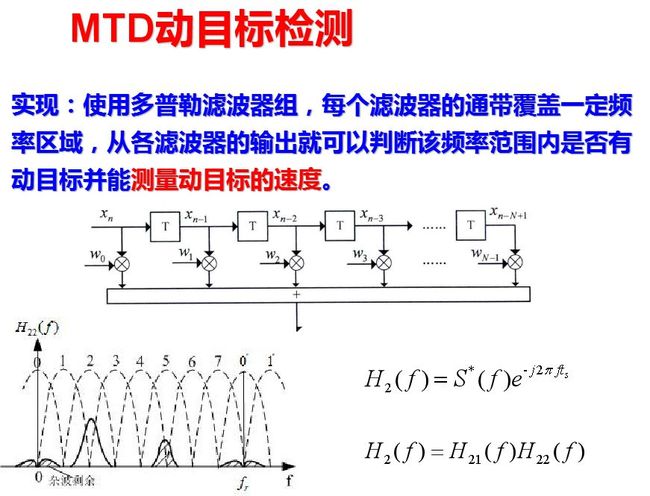
式中, H21(f)为单个脉冲的匹配滤波器, 通常在接收机中放实现; H22(f)是对相参脉冲串进行匹配滤波, 它利用了回波脉冲串的相参性而进行相参积累; H22(f)是梳齿形滤波器, 齿的间隔为脉冲重复频率fr, 齿的位置取决于回波信号的多普勒频移, 而齿的宽度则应和回波谱线宽度相一致。
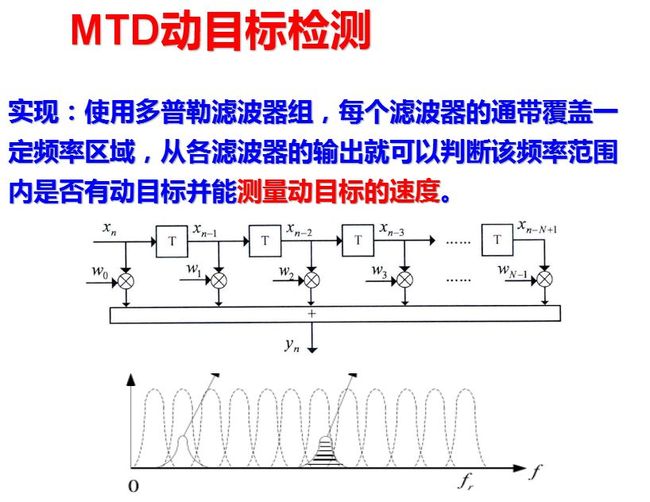
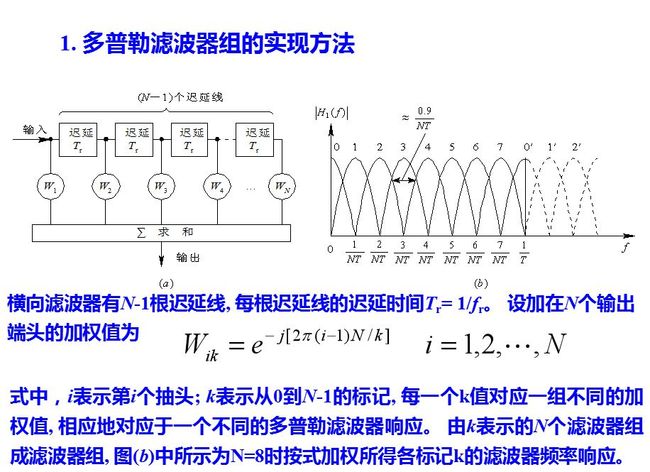
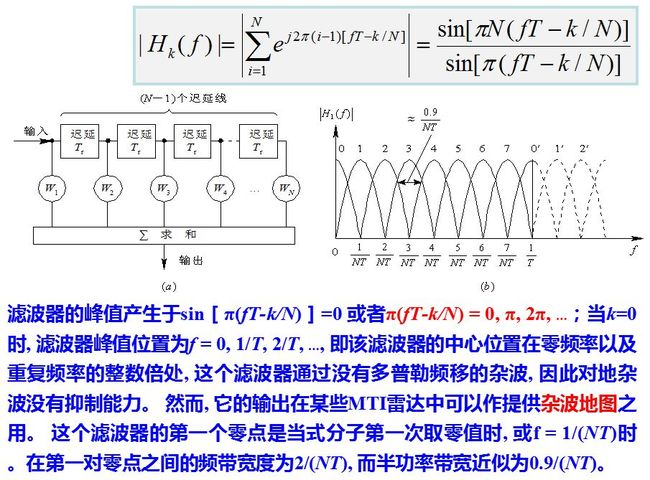
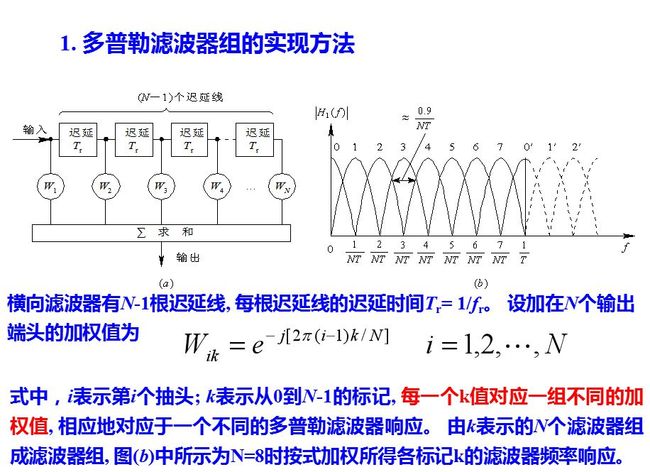
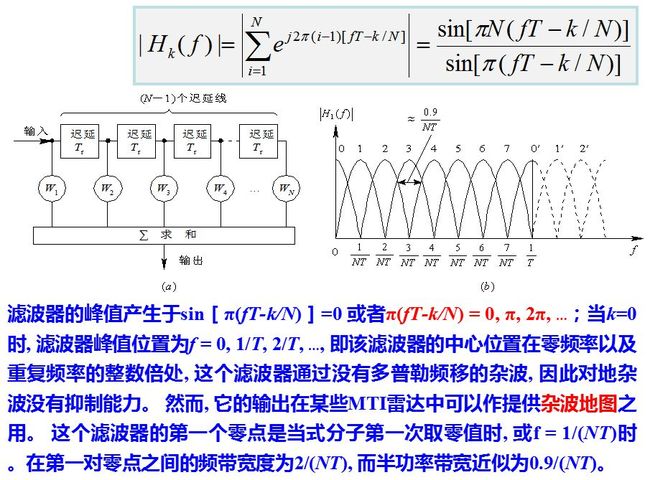
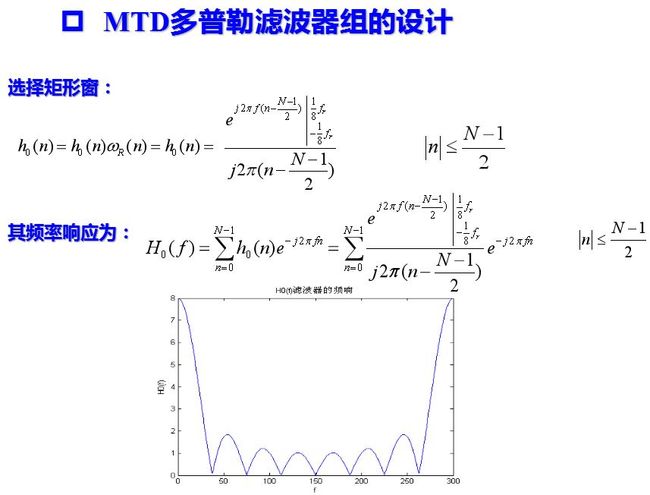
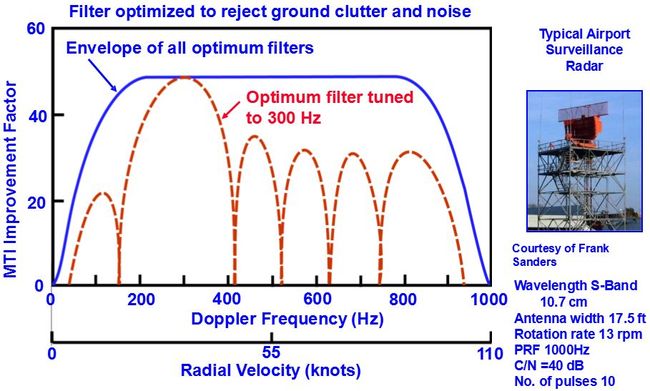
要对回波相参脉冲串作匹配滤波, 必须知道目标的多普勒频移以及天线扫描对脉冲串的调制情况(亦即信号的时宽, 它决定信号的频宽)。在实际工作中, 多普勒频移fd不能预知, 因此需要采用一组相邻且部分重叠的滤波器组, 覆盖整个多普勒频率范围, 这就是窄带多普勒滤波器组,如图所示。
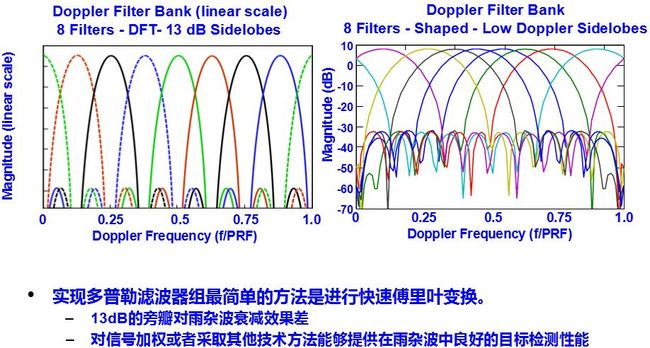
式中, s(i-1)T)为横向滤波器从输入开始各点的信号值。式就是进行离散傅里叶变换的表述式, 因此当N是2的乘方时(例如N=2, 4, 8, 16, …), 可以用快速傅里叶变换(FFT)的算法来完成式(8.6.8), 亦即用FFT实现N个滤波器组, FFT算法差不多只要做(N/2) log2N个乘法运算, 就可以明显地节省处理所需的运算量。
用横向滤波器来实现窄带滤波器组时, 可以不采用式所示的权值而是根据特定的需要灵活地选用不同的加权矢量, 这样, 设计者就能根据要求在不同频率处设置特性相异的滤波器。单个滤波器的设计对低副瓣要求和主瓣展宽之间要折衷考虑, 通常在零多普勒频率即地杂波所在处对低副瓣有更高要求。滤波器数目的选择则要综合考虑硬件复杂度和滤波器间允许的跨接损失两个因素而定。
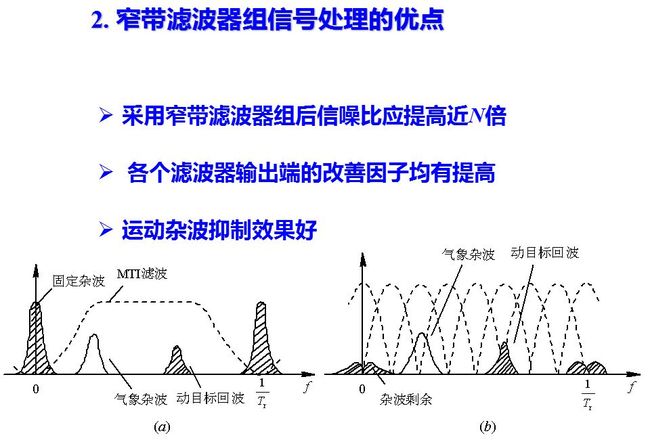
在用均匀排列的滤波器组时, 每个窄带滤波器只占迟延线对消器通频带的大约1/N宽度, 因而其输出端的信噪比有相应的提高。对于“白色”噪声(含由于系统不稳所产生者), 采用窄带滤波器组后信噪比应提高近N倍。对于有色杂波来讲, 各个滤波器输出端的改善因子均有提高(与迟延对消器比较), 但提高的程度是不相同的: 越靠近杂波中心的滤波器, 其改善程度愈差; 杂波谱越宽, 各滤波器的改善程度也变差。采用窄带滤波器组之所以能较MTI对消器提高改善因子,是因为它把频带细分后, 各滤波器的杂波输出功率只有各自通带范围内的杂波谱部分, 而不是整个多普勒频带内的杂波功率。
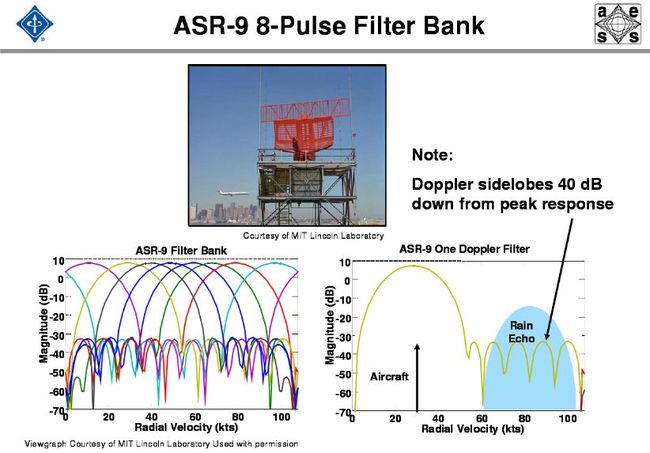
但要注意到, 杂波不仅由各滤波器的主瓣进入, 而且未加权的滤波器由于其副瓣值较高(-13.2dB)而副瓣的频率位置又处于强杂波处, 这时由副瓣进入的杂波将明显地降低其改善因子。解决的办法可以有两种, 一种是在窄带滤波器组前面先采用对消器(一次或二次), 将杂波的主要部分滤去, 这样后接的滤波器组中通过副瓣进入的杂波明显减少, 各滤波器的改善因子会提高。这种方法实际上常用, 因为滤去强杂波后, 滤波器组的动态范围可明显减小, 利于技术实现。第二种办法是采用加权法降低各个滤波器的副瓣, 同样可以提高改善因子,所付代价是滤波器的主瓣有所加宽。
展开谱线的宽度反比于天线照射目标的时间。
杂波图的存储,将雷达所监视的空间按照距离和方位分割成许多空间单元,每个空间单元的距离长度相当于一个脉冲宽度或者稍大些,方位宽度相当于半个波瓣宽度或者稍大。
低杂波图随着实际情况及时进行更新,使用“时间单元平均”的杂波图作为检测切向飞行目标用,即以一个天线扫描周期作为一个单元,每个空间单元存储的应该是多次天线扫描所得杂波的平均值。
![]()
在用均匀排列的滤波器组时, 每个窄带滤波器只占迟延线对消器通频带的大约1/N宽度, 因而其输出端的信噪比有相应的提高。对于“白色”噪声(含由于系统不稳所产生者), 采用窄带滤波器组后信噪比应提高近N倍。对于有色杂波来讲, 各个滤波器输出端的改善因子均有提高(与迟延对消器比较), 但提高的程度是不相同的: 越靠近杂波中心的滤波器, 其改善程度愈差; 杂波谱越宽, 各滤波器的改善程度也变差。采用窄带滤波器组之所以能较MTI对消器提高改善因子,是因为它把频带细分后, 各滤波器的杂波输出功率只有各自通带范围内的杂波谱部分, 而不是整个多普勒频带内的杂波功率。
但要注意到, 杂波不仅由各滤波器的主瓣进入, 而且未加权的滤波器由于其副瓣值较高(-13.2dB)而副瓣的频率位置又处于强杂波处, 这时由副瓣进入的杂波将明显地降低其改善因子。解决的办法可以有两种, 一种是在窄带滤波器组前面先采用对消器(一次或二次), 将杂波的主要部分滤去, 这样后接的滤波器组中通过副瓣进入的杂波明显减少, 各滤波器的改善因子会提高。这种方法实际上常用, 因为滤去强杂波后, 滤波器组的动态范围可明显减小, 利于技术实现。第二种办法是采用加权法降低各个滤波器的副瓣, 同样可以提高改善因子,所付代价是滤波器的主瓣有所加宽。
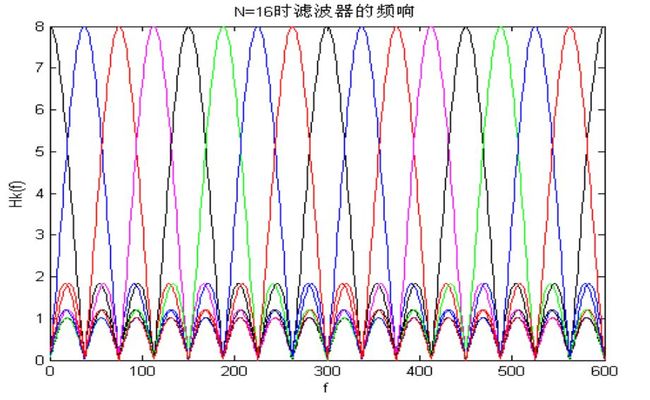
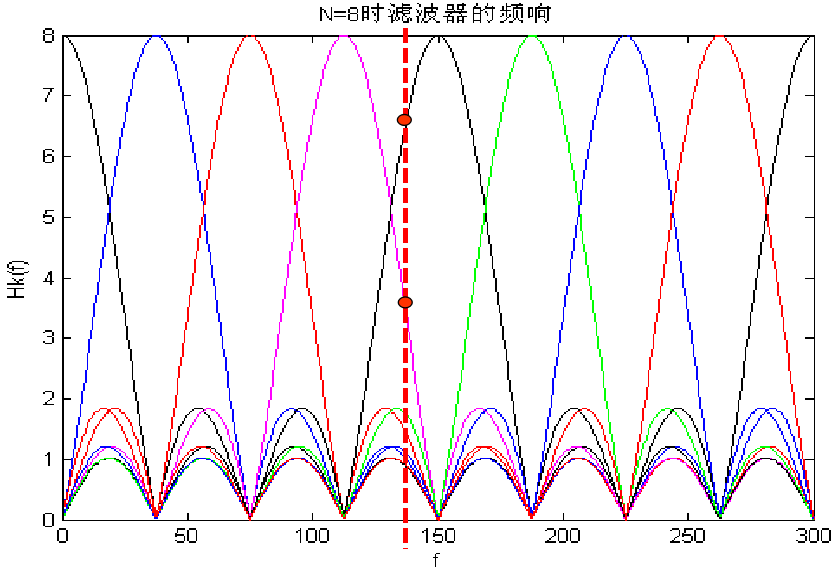
随着FFT点数的增多,滤波器的频率分辨率也在增大,也即雷达对速度的分辨率也越高。但是,随着FFT点数的增多,系统的运算量也在增大,这会影响系统的实时性。对FFT点数的选择需要综合系统对速度分辨率和实时性的要求以及雷达一个扫描周期内收到的回波数等因素来决定。
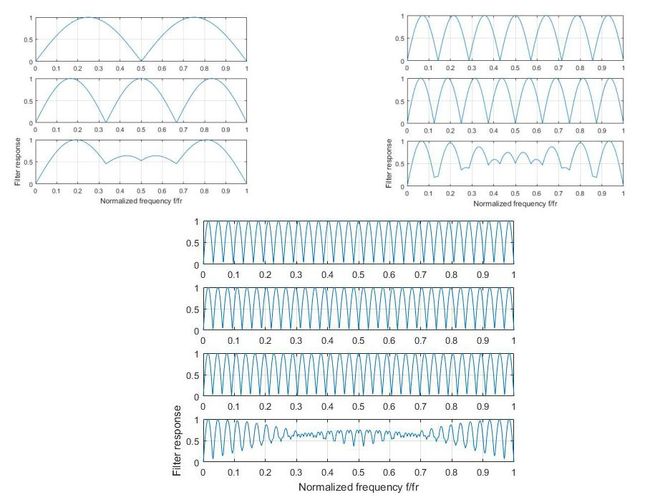
图3.4和图3.5体现出滤波器在全频段内都没有截止特性,这是一个误区,因为上述的任意一幅图都是由很多滤波器组成的,也就是说,8点FFT点数的滤波器是由8个滤波器组成的,16点FFT点数的滤波器是由16个滤波器组成的,同样,32点FFT点数的滤波器是由32个滤波器组成的。在实际的应用过程中,系统把回波信号最强的滤波器的输出作为真实的目标信号。为了说明这个问题。下面分别绘出8点FFT和16点FFT真实工作时的滤波特性。
但FFT滤波器在零频和脉冲重复频率整数倍处没有凹陷,所以无法抑制静态杂波,需要考虑其他方式帮助解决。可以考虑添加MTI对消器,或者将静态杂波对应的滤波器通道的输出去除。
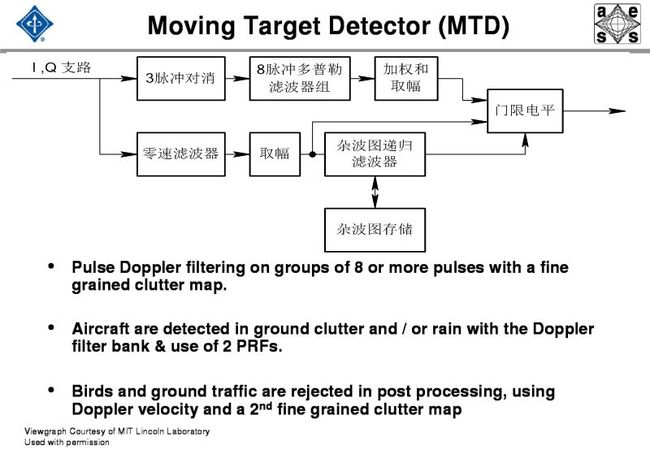
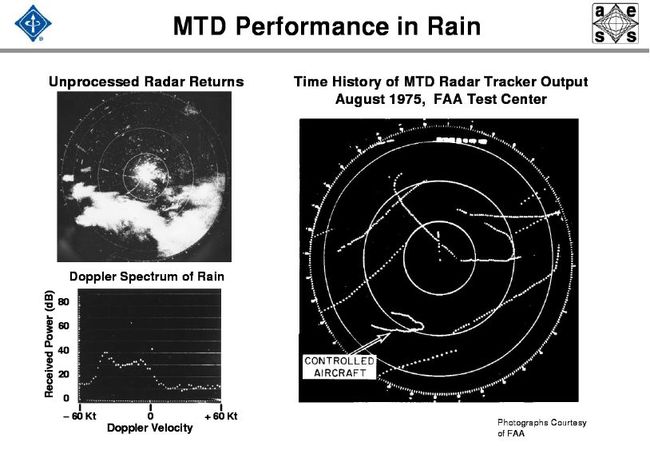
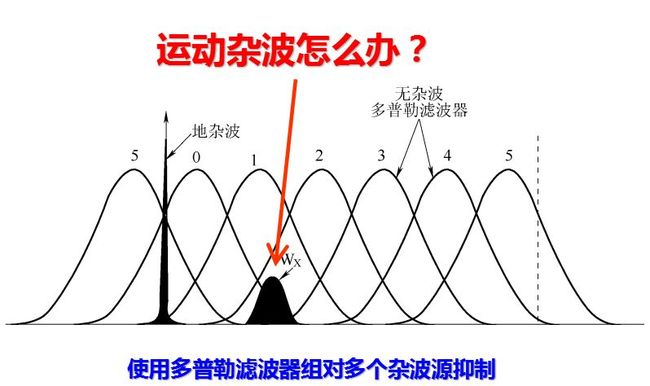
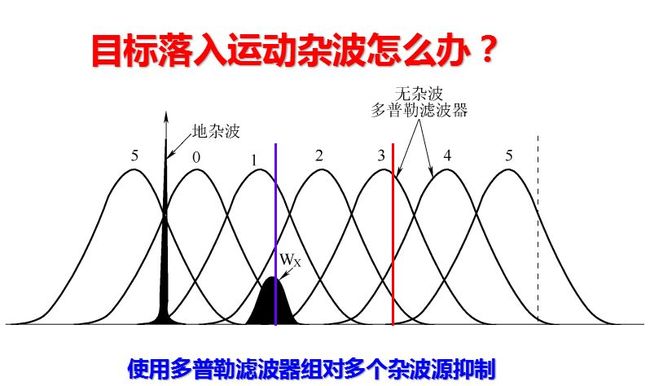
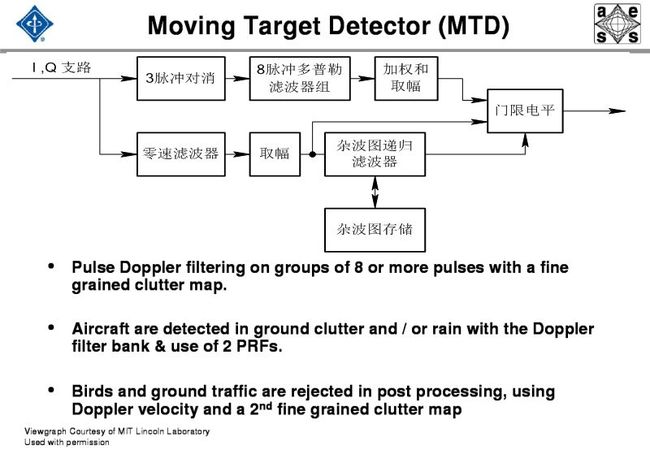
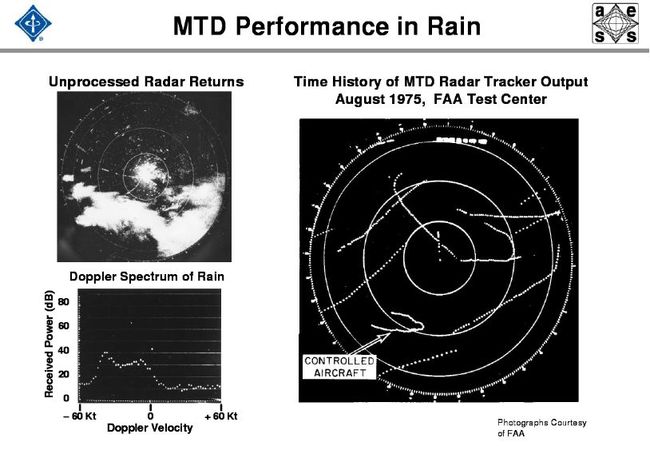
基于MTI原理,在MTD中,信号处理机使用若干个并行的多普勒滤波器、CFAR处理及为抑制点杂波剩余而增加的一个或多个高分辨力的杂波图,可进一步提高处理机的线性动态范围。在现代警戒雷达中,由于增加了这些处理方法,因此已能实现一个完整的信号处理系统,从而获得良好的杂波抑制。图15.6给出了这种MTD处理系统的一个典型实现方法。每个多普勒滤波器所设计的目标响应都是其多普勒频带中的非重叠部分,并且也抑制掉其他多普勒频率内的所有杂波源。这种方法使每个滤波器的相关信号积累最大,与单个MTI滤波器相比,可在更宽的多普勒频域内实现更大的杂波衰减。因此,一个或多个杂波滤波器能抑制掉不同多普勒频率的多个杂波源。图是MTD多普勒滤波器组抑制同时存在的地杂波和气象杂波(Wx)的一个实例。从图中可看出,滤波器3和4能明显抑制这两个杂波。
![]()
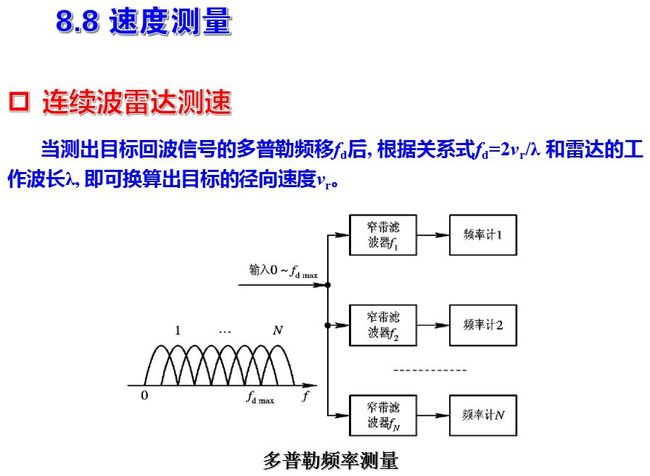
连续波雷达测速的原理框图已如图所示。图中相位检波器输出经低通滤波器取出多普勒频率信号送到终端测量和指示。低通滤波器的通频带应为Δf到fdmax, 其低频截止端用来消除固定目标回波, 同时应照顾到能通过最低多普勒频率的信号; 滤波器的高频端fdmax则应保证目标运动时的最高多普勒频率能够通过。连续波测量时, 可以得到单值无模糊的多普勒频率值。
如果要测量多普勒频率的正负值, 则图中的二次检波器应采用正交双通道处理,以避免单路检波产生的频谱折叠效应。
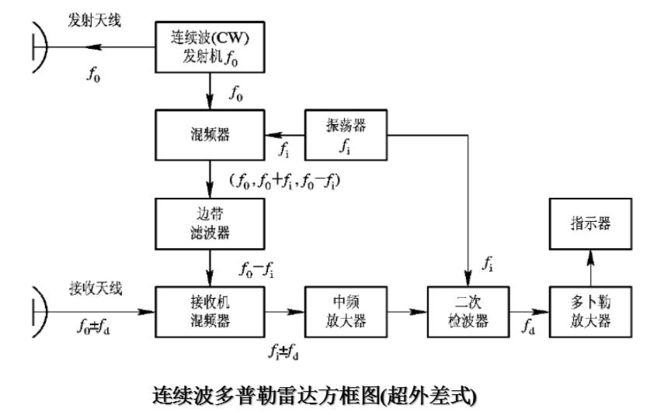
连续波多普勒雷达可用来发现运动目标并能单值地测定其径向速度。利用天线系统的方向性可以测定目标的角坐标, 但简单的连续波雷达不能测出目标的距离。这种系统的优点是: 发射系统简单, 接收信号频谱集中, 因而滤波装置简单, 从干扰背景中选择动目标性能好, 可发现任一距离上的运动目标, 故适用于强杂波背景条件(例如在灌木丛中蠕动的人或爬行的车辆)。由于最小探测距离不受限制, 故可用于雷达信管, 或用来测量飞机、 炮弹等运动体的速度。
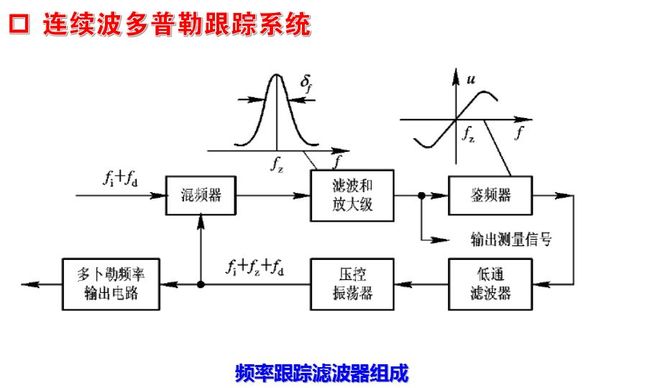
1) 频率跟踪滤波器 跟踪滤波器的带宽很窄(和信号谱线相匹配), 且当多普勒频率变化时, 滤波器的中心频率也跟随变化, 始终使多普勒频移信号通过而滤去频带之外的噪声。图画出了跟踪滤波器的组成方框图, 这就是一个自动频率微调系统。输入信号的频率为fi+fd(fi为固定目标回波的频率), 它与压控振荡器输出信号在混频器差拍后, 经过放大器和滤波器送到鉴频器。如果差拍频率偏离中频fz, 则鉴频器将输出相应极性和大小的误差控制电压, 经低通滤波器后送去控制压控振荡器的工作频率, 一直到闭环系统工作达到稳定, 这时压控振荡器的输出频率接近于输入频率和中频之和。压控振荡频率的变化就代表了信号的多普勒频率, 因而从经过处理后的压控振荡频率中即可取出目标的速度信息。
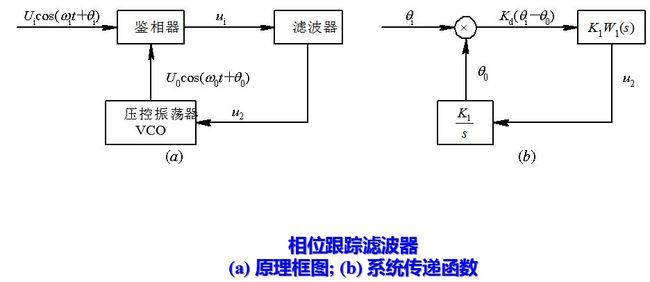
2) 锁相跟踪滤波器 频率跟踪滤波器是一个一阶有差系统, 因为系统中没有积分环节。可以采用锁相回路来得到无稳态频偏的结果。相位差是频率差积分的结果, 只有频率差等于零时才能得到固定的相位差。锁相回路的组成及其系统传递函数如图所示。设输入信号为Uicos[(ωi+Δωi )t+φi], 其相角增量为θi = Δωi t +φi; 而压控振荡器输出电压为U0cos[ (ω0 + Δω0)t +φ0], 其相角增量为θ0 = Δω0t +φ0。鉴相器的输出是输入相角θi和输出相角θ0之差的函数, 当其相角较小时, 可用线性函数表示, 这时输出电压u1=Kd(θi-θ0)。
由于频率是相位的导数, 而误差电压u2直接控制压控振荡器的频率, 故对输出相角θ0来讲, VCO相当一个积分环节。系统稳定工作后有相位误差θe=θi-θ0而没有频率误差。因此,将锁相回路用作跟踪滤波器时, 由压控振荡器输出的频率中取出多普勒频率, 将没有固定的频率误差。但用锁相回路时要求压控振荡器(VCO)的起始装定值更接近输入值, 且目标的运动比较平稳。
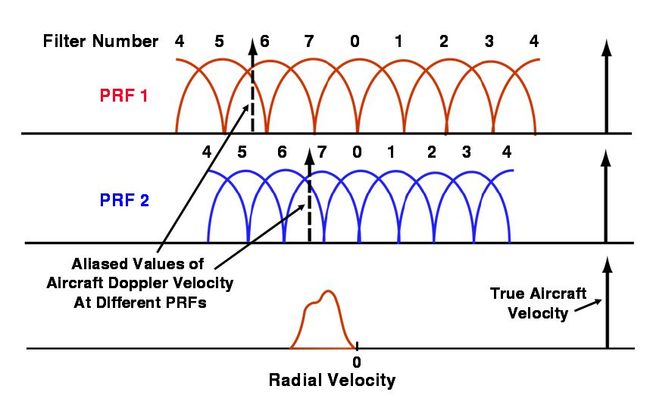
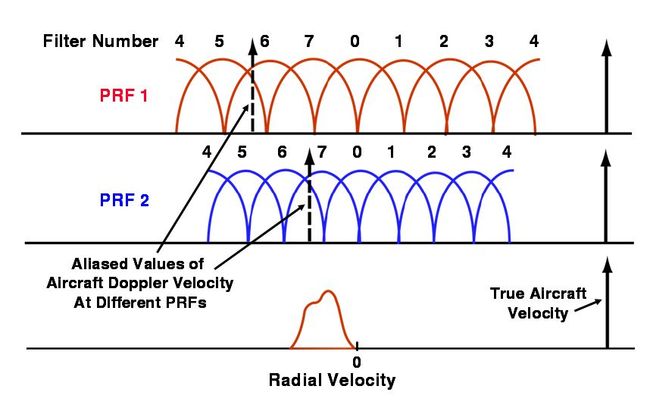
有时雷达重复频率的选择不能满足不模糊测速的要求, 即由窄带滤波器输出的数据是模糊速度值。要得到真实的速度值, 就应在数据处理机中有相应的解速度模糊措施。解速度模糊和解距离模糊的原理和方法是相同的。
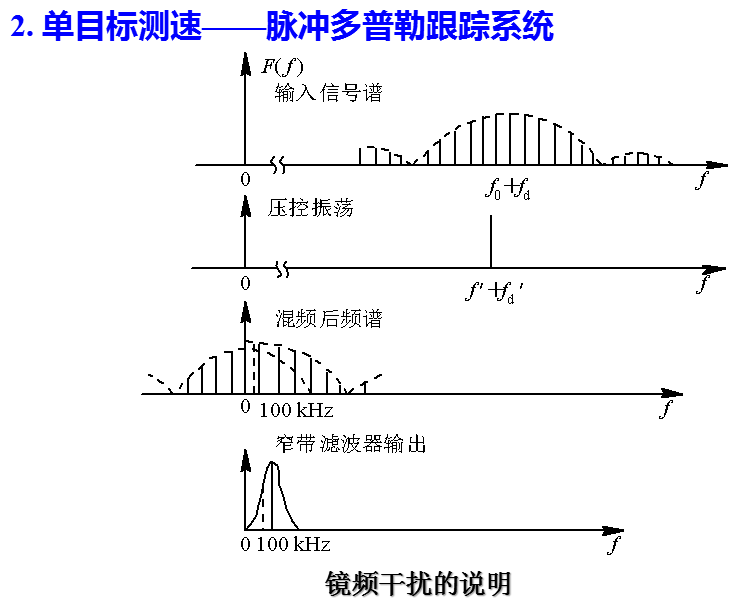
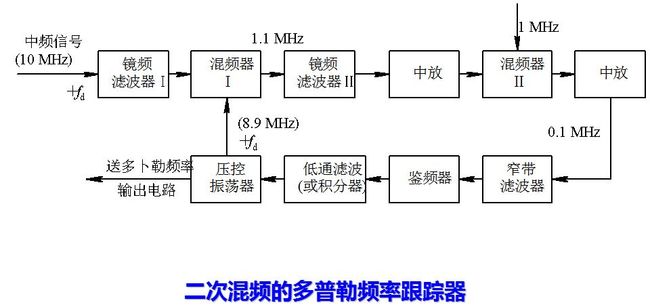
和连续波测速时不同, 脉冲雷达测速时将存在速度模糊, 即跟踪回路不是跟在中心谱线而是跟在旁边的谱线上, 压控振荡器输出的频率增量Δf=fd±nfr。因此首先要判断是否有模糊。可以用距离的微分量来作为比较的标准, 这个量作为速度虽然精度不高但却是单值的, 只要其相应于多普勒频率的测量误差小于(1/2) fr, 即Δfd= (2/λ)·Δvr<(1/2) fr即可。将测距系统送来的微分量和测速回路的输出量加以比较, 求出测速回路的模糊值n, 然后用适当的方式指令测速回路压控振荡器, 强制其频率突变nfr值, 使得压控振荡器频率和信号的中心谱线之差能通过窄带滤波器, 让系统跟踪在信号的中心谱线上, 这样, 把压控振荡器的输出送到多普勒频率输出设备就可以读出不模糊的速度值。