python量化：如何利用tushare构造FF三因子模型？

笔者是一枚大二菜狗，最近刚上完学院开的python金融量化的选修课，挣扎了几日交完了课程作业，但总觉得有点白瞎了tushare的2000积分。最近刚好看了FF的三因子模型，于是便对着投资学课本与知乎试着用代码来构建FF的三因子。文章里不含对三因子模型的检验与回归，仅仅作为对自己学习的一个记录，如果有任何地方不太严谨，还请各位大佬包容指正。

FF三因子模型介绍

FF三因子模型最初是由Fama和French在1993年提出（具体可参照论文Common risk factors in the returns on stocks and bonds），模型如下：
其中，rf是无风险利率，SMB是指做多小市值公司而做空大市值公司得到的组合收益率（根据小市值效应），HML是做多高账面价值比而做空低账面价值比公司的到的组合收益率（根据市净率指标），而MKT则是市场投资组合的超额收益率。
尽管FF三因子模型经过如此多年的实证检验已经被证实无效，但它作为多因子模型的鼻祖，对当今的量化投资的入门仍有极大的借鉴意义。

代码实现

代码的实现主要分为：数据调取->数据处理->构建因子。注意：笔者在数据处理时省略了构建前的数据清洗，并未对相应的ST股票进行完全剔除（emmm这个等我学学再来补坑），仅对空缺的股票数据值进行了简单填充。

从tushare调取数据

笔者对因子构建的时间选在了2020年的5月初到2021年的年末，构建频率按照日频。在调取数据前我们要明确FF三因子模型分别需要对SML（市值因子）、HML（账面市值比因子）与MKT（市场指数因子）进行构建 ，因此我们需要的数据分别有全部上市公司股票每日的收盘价、市净率（用以代替账面市值比BM）、总市值、沪深300的每日收益率（用以描述市场指数收益率）与无风险利率（从中国资产管理中心获得为0.000041）。而以上数据均可从强大的tushareAPI调取获得（详细的调用方法可参见tushare的官网https://tushare.pro/）。
代码实现：

#导入必要的库
import pandas as pd
import tushare as ts
import seaborn as sns
import matplotlib as mpl
import matplotlib.pyplot as plt 
from tqdm import tqdm, trange  #进度条可视化
import datetime
import time

#####构造因子前的数据获取#####
#接入tushare API
pro = ts.pro_api()  
#定义函数获取每日指标
def get_daily_basic(stock_codes,start_date,end_date):  #参数类型：list,string,string
    df = pro.daily_basic(ts_code=[''], start_date='', end_date='')  #生成一个空的dataframe
    pbar = tqdm(stock_codes)
    for codes in pbar:
        st = time.time()
        pbar.set_description('Processing '+codes)
        df1 = pro.daily_basic(ts_code=codes, start_date=start_date, end_date=end_date)
        df = pd.concat([df,df1],ignore_index=True) 
        et = time.time()
        t = et-st
        if t<0.3:
            time.sleep(0.3-t)
    return df

#市场指数收益率:选取沪深300指数 399300.SZ
index_daily = pro.index_daily(ts_code='399300.SZ', start_date='20200506', end_date='20220101').sort_values('trade_date').reset_index()

#获取所有上市公司股票列表
stocks_listL =pro.stock_basic(exchange='', list_status='L', fields='ts_code,symbol,name,area,industry,list_date,delist_date')
stock_codes = stocks_listL['ts_code'].tolist()
#获取所有上市公司的每日指标
data = get_daily_basic(stock_codes,'20200505','20220101')
data.to_csv("d:\\daily_basic_2020_to_2022.csv")  #数据量过多，存到本地方便调用

于是我们获得了这样庞大的一个矩阵（自己写的调用函数是按每只股票来循环访问接口，因为tushare接口对分钟调用次数的限制，所以调用速度较慢，于是顺手封装了个进度条tqdm来可视化）。
接下来我们要做的就是对缺失的数据进行简单填充（非常简单粗暴…）。

data.fillna(method='ffill', axis=0, inplace=False)

利用数据构建因子

根据FF三因子的构建逻辑（详细见Fama and French 1993）,我们需要将个股按照每年五月末的市值分为两组，前50%是Big组，后50%是Small组；同时按照BM账面市值比分为三组，前30%是High组，后30%是Low组，其余的都是Medium组；一旦分组形成，以年为周期不发生改变，直到下一年末再重新分组。但是，我国上市公司企业年报的披露一般都在4月末，因此在构建因子时我们应当选用5月初的数据来分组。
首先，我们定义一个函数mark_FF_group(df)来对股票所在的组合进行标记：

#（按市值分为Small与Big两组，分别为50%；按照账面市值比BM分为30%，40%，30%的H,M,L组）
def mark_FF_group(df):
    #输入的dataframe为每年五月初的数据（我国的上市公司年报一般在4月底公布）
    #1.标记H,M,L;
    df['group_BM'] = 'M'  #初始化分组为'M'
    df.loc[df['BM']>=df['BM'].quantile(0.7),'group_BM'] = 'H'  #前30%划分为'H'
    df.loc[df['BM']<df['BM'].quantile(0.3),'group_BM'] = 'L'  #后30%划分为'L'
    
    #2.标记SIZE;
    df['group_SIZE'] = 'S'  #初始化分组为'S'
    df.loc[df['mkt']>=df['mkt'].quantile(0.5),'group_SIZE'] = 'B'  #前50%划分为'B'
    
    #3.分别划分为 B/H, B/M, B/L, S/H, S/M, S/L 六个组合
    df['portflio_mark'] =df['group_SIZE'] +'/'+df['group_BM']
    
    return df

接着我们从获取的每日指标数据data中选出2020年5月初的部分，命名为data_20_5，并进行标记：

data_20_5 = pd.DataFrame(data[data['trade_date']==20200506], columns=['trade_date','ts_code','close','pb','total_mv']).rename(columns={'total_mv':'mkt'}).reset_index(drop=True)
data_20_5['BM'] = data_20_5['pb'].apply(lambda x : 1/x)
mark_FF_group(data_20_5)

按照同样的方法我们对2021年5月初的数据进行筛选分组标记，命名为data_21_5，并将标记得到两年的数据使用concat()函数进行合并：

#合并两年数据并标记
data_5 = pd.concat([data_20_5,data_21_5],ignore_index=True).reset_index(drop=True)
data_5['portflio_date'] = data_5['trade_date'].apply(lambda x:x//100)
data_5

于是我们使用merge()函数按照年份将分组完成的标记并入原来的数据data中：

#将标记好的数据与股票数据合并merge()
data_rt = pd.DataFrame(data,columns=['trade_date','ts_code','close','total_mv']).rename(columns={'total_mv':'mkt'}).reset_index(drop=True)
data_rt['portflio_date'] = data_rt['trade_date'].apply(lambda x:x//10000*100+5 if (x//100%10>=5) or (x//1000%10==1) else (x//10000-1)*100+5)
data_rt = pd.merge(data_rt,data_5.drop(['trade_date','BM','mkt','pb','close'],axis=1),how='inner',left_on=['ts_code','portflio_date'],right_on=['ts_code','portflio_date'])
data_rt

(细心的读者可能会发现下面经过合并过的数据的列数与上文从tushare调用的数据有所出入，特别说明一下笔者最初调用数据的start_date为20200101，但实际202005前的股票组合属于201905的分组，因此实际上笔者的构建时期是202005~202112)

接下来我们根据收盘价序列计算得到个股的收益率：

#股票的收益率序列
data_rt = data_rt.sort_values(by='trade_date',ascending=True)
data_rt['ret'] = data_rt.groupby('ts_code')['close'].apply(lambda x:x.pct_change()).dropna()
data_rt

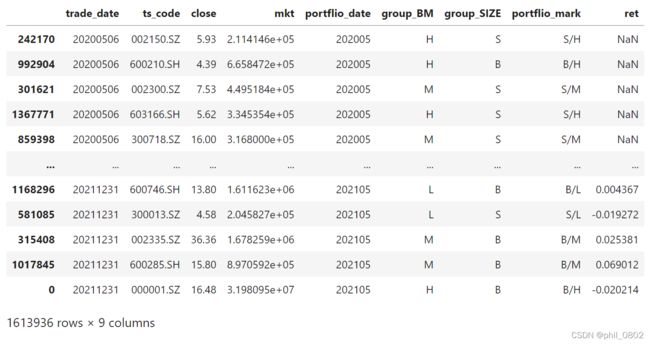
于是，在我们掌握了股票的日频收益率、每个周期的组合标记后，我们便可以开始计算按照BM值与市值划分的六种组合（B/H, B/L, B/M, S/H, S/L, S/M）的投资收益率了：

#20200506才进行建仓划分，故该日收益率ret为0
data_rt.loc[data_rt.trade_date==20200506,'ret']=0

#将每个月按照SIZE与BM分组，计算组内各支股票收益率市值加权综合收益率
port_ret = data_rt.groupby(['trade_date','portflio_mark']).apply(lambda x: (x['ret']*x['mkt']).sum()/x['mkt'].sum())
port_ret = port_ret.reset_index()  #重新设置索引
port_ret.rename(columns={port_ret.columns[-1]:'ret'},inplace=True)  #重新设置列名
port_ret=port_ret.pivot(index='trade_date',columns='portflio_mark',values='ret')  #将表格改为透视表
port_ret

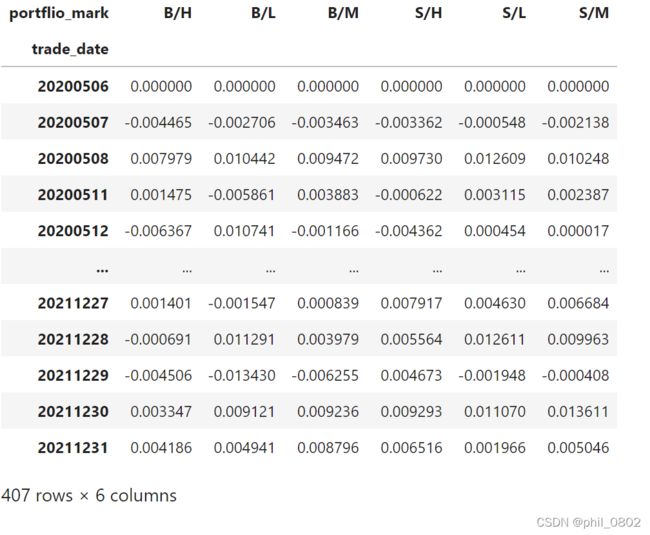
那么到这里我们已经获得了6个投资组合在周期内的投资收益率了。接下来最重要的一步就是根据SMB与HML的计算公式来进行因子的构建：
市值因子SMB的计算公式：SMB = （SL + SM +SH）/3 -(BL + BM +BH)/3

port_ret['SMB']=(port_ret['S/L']+port_ret['S/M']+port_ret['S/H'])/3-(port_ret['B/L']+port_ret['B/M']+port_ret['B/H'])/3

BM因子HML的计算公式：HML = (SH + BH)/2 - (SL + BL)/2

port_ret['HML']=(port_ret['S/H']+port_ret['B/H'])/2-(port_ret['S/L']+port_ret['B/L'])/2

得到SMB与HML因子的计算序列：

ff3=port_ret.loc[:,['SMB','HML']].copy()
ff3=ff3.reset_index()
ff3.columns=['tradedate','SMB','HML']
ff3

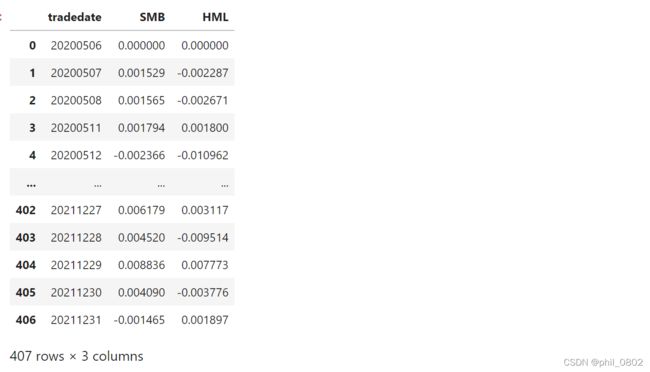
在因子序列中加入市场指数收益率mkt_rf与无风险利率rf的序列：

# index_daily
ff3['mkt_rf'] = index_daily['pct_chg'].copy().apply(lambda x:x/100)
#无风险利率rf=0.000041
ff3['rf'] = 0.000041
ff3

三因子模型序列构建完成。

总结

经过几日的研究与调试，也算终于能够把三因子模型用代码实现出来了。
从计量的角度来看，因子模型是投资组合的收益率作为解释变量来对股价进行回归检验。其实三因子组合构建本身所体现的思想并不难理解，本质上是将市场上的股票按照一定指标进行分组，构建投资组合，计算各个投资组合得到的收益率，以此得到因子。
但是在用python实现时，我发现遇到最大的几个问题便是：数据获取的类型；如何处理清洗得到的数据；对pandas库dataframe的处理仍旧不熟练，特别是merge()函数、groupby()函数的运用。作为一名刚刚入坑python金融量化的小白，我还有太多东西需要去学习。也愿自己在接下来的日子里继续加油哦！

参考链接：
[1]:股票多因子模型的回归检验 https://zhuanlan.zhihu.com/p/40984029
[2]:Fama-French三因子模型（附代码）https://zhuanlan.zhihu.com/p/374959531
[3]:Python实现Fama French三因子模型 https://zhuanlan.zhihu.com/p/190028494
[4]: 《投资学》(美)滋维·博迪 亚历克斯·凯恩 艾伦J.马库斯