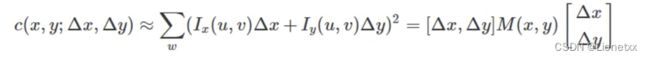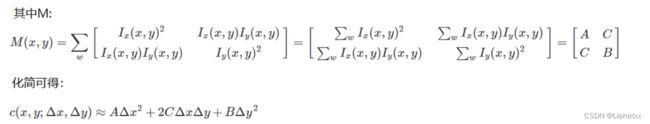OpenCV：10特征检测
特征检测的基本概念
特征检测是计算机视觉和图像处理中的一个概念。它是指使用计算机提取图像信息，决定每个图像的点是否属于一个图像特征。特征检测的结果是把图像上的点分为不同的子集，这些子集往往属于孤立的点、连续的曲线或者连续的区域
特征检测包括边缘检测、角检测、区域检测和脊检测
特征检测应用场景：
- 图像搜索，比如以图搜图
- 拼图游戏
- 图像拼接
- …
以拼图游戏为例来说明特征检测的应用流程
- 寻找特征
- 特征是唯一的（如果每个地方都有该特征，那我们就无从下手了）
- 特征是可追踪的
- 特征是能比较的
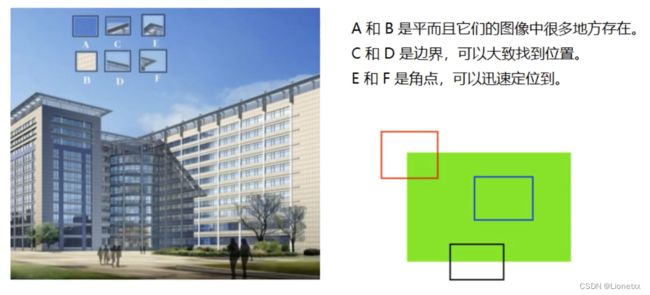
因此：
A、B（蓝色框）不是特征 ——> 不是唯一的
C、D（黑色框）不是特指 ——> 不是唯一的
E、F（红色框）是特征 ——> 唯一、可追踪、能比较
我们发现：
- 平坦部分（A、B）很难找到它在原图的位置
- 边缘部分（C、D）相对平坦部分好找一些，但是无法唯一确定
- 角点（E、F）可以一下就找到其在原图中的位置 ——> 角点不是边缘！而是拐角
图像特征就是值有意义的区域，具有独特性、易于识别性
Harris角点检测
在图像特征中最重要的就是角点，哪些是角点呢？
- 灰度梯度最大值对应的像素（附近是不同的颜色！如高楼边角一边是墙壁的颜色一边是天空的颜色）
- 两条线的交点（两个边缘就是两条线）
- 图像中灰度值的极值点（一阶导数最大，二阶导数为0）
三幅图对应三种情况：
图一在平坦位置向四周移动，灰度值变化都不大；图二上下移动灰度值变化不大，左右移动灰度值变化剧烈；图三无论朝着哪个方向移动，灰度值都剧烈变化
原理
图像I(x,y)，当在点(x,y)处平移(△x,△y)后的自相似性：
自相似性：移动后与原来点相似度有多少，其实就是差异；具体是上一个位置框的像素值 - 下一个框的像素值
加平方是因为我们只在变化量的大小，而不在乎灰度值变量还是变暗
我们的框框相当于一个卷积核，而卷积核对应每一个位置的像素都有一个权重，因此w(u,v)是这个像素框自带的权重（高斯加权：越靠近中心位置，加权系数越大）
我们需要把I(u + △x,v + △y)用泰勒公式展开，对图像图像I(x,y)在(x,y)处平移(△x,△y)后进行一阶近似：
其中Ix、Iy是图像I(x,y)的偏导数
补充泰勒公式：
一般我们用到二阶即可
近似可得：
二次项函数本质是一个椭圆函数，方程为：
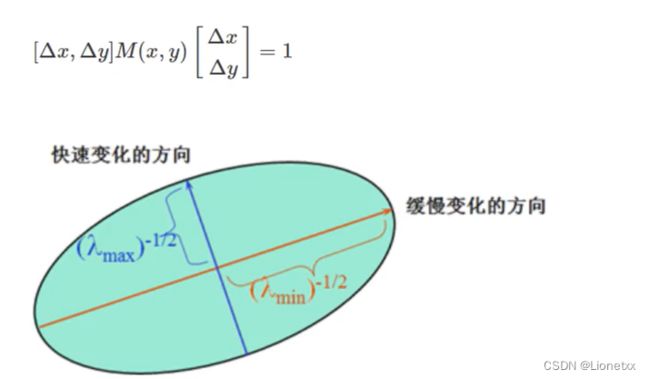
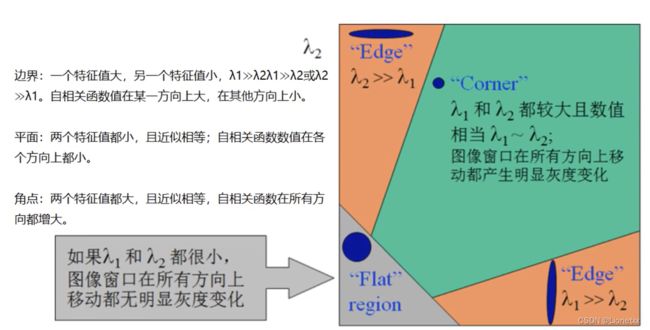
即λ越大，图像灰度值变化越大（其中λ1、λ2分别为矩阵M中：λ1 = 1 / A²、λ2 = 1 / B²）
我们总不可能再去手动比较λ1、λ2吧，那也太蠢了
opencv提供了API，这也是我们调用Harris角点检测的返回值：
角点响应：
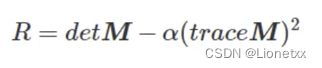
其中detM = λ1 × λ2 ，traceM = λ1 + λ2 ，α = 0.04 ~ 0.06（自己选择）
角点响应结果：返回值
-
0 < R < 1，为平面部分：如λ1 = 0.01 ；λ2 = 0.02（λ1、λ2都很小），有
-
R < 0，为边缘部分：如λ1 = 100 ； λ2 = 0.01（λ1、λ2中一个远大于另一个），有
-
R >> 0，为角点部分 ：如λ1 = 100 ； λ2 = 101（λ1、λ2都很大且数值相当），有
应用
检测窗口在图像中移动，上图对应着三种情况
- 在平坦区域移动：无论朝着哪个方向移动，衡量系统变换不大
- 在边缘区域移动：垂直边缘方向移动时（往里走或往外走），衡量系统变换剧烈
- 在角点区域移动：无论往哪个方向移动，衡量系统都变换剧烈
关键API：cv2.cornerHarris(src, blockSize, ksize, k[, dst[, borderType]])
其中：
src：操作的图片（必须是灰度图）blockSize：检测窗口的大小（没有要求必须是奇数，我们不是做卷积操作），设置的值越小越能检测出角点，值太大的话会扫描的一大块，不好检测ksize：Sobel算子的大小（原理处用到了偏导数，Sobel算子就是用于计算偏导数的）k：相当于角点响应公式中的α，取值为0.04 ~ 0.06（默认值为0.04 ）
import cv2
import numpy as np
img = cv2.imread('./chess.png')
# img = cv2.imread('./hand.png')
# 变成灰度图片
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
##----------------------------------------------------------
# 角点检测 ——> 返回角点响应R，每一个像素都可以计算出一个角点响应
R = cv2.cornerHarris(gray,blockSize = 2,ksize = 3,k = 0.04)
# 显示角点
# 设定阈值来判断角点 怎么设置？
# 返回值R中有一个最大的R值R.max()，即最大的角点响应，但我们不可能只用最大的角点，因为我们还有很多个角点，所以我们找一个关系来设置阈值
# R > ( 0.01 * R.max()) # 用ndarray和单个数字相比，返回值为bool类型：该点的角点响应大于最大角点响应的0.01倍，我们认为它就是角点
# 我们把它作为一个条件，直接对图片进行筛选
img[R > ( 0.01 * R.max() )] = [0,0,255] # 颜色改成红色
##----------------------------------------------------------
cv2.imshow('img',img)
cv2.waitKey(0)
cv2.destroyAllWindows()
图片的角点响应
与角点响应阈值做比较，大于就是True，小于就是False：R > ( 0.01 * R.max() )
将R > ( 0.01 * R.max() )作为条件img[R > ( 0.01 * R.max() )]直接对图片进行筛选，将满足角点要求的像素点筛选出来，有：
把这些点都赋值为红色(0,0,255)
结果：
