多元时间序列预测之(二)LSTNet模型
文章目录
- LSTNet论文解读
-
- 1. 问题定义
- 2. 模型解读
-
- 2.1 卷积组件
- 2.2 递归组件
- 2.3 递归-跳过层
- 2.4 时间注意力层
- 2.5 自回归组件
LSTNet论文解读
本文作为第二讲,讲述使用常规深度学习方法做多元时间序列预测的模型。由于近年图神经网络的兴起,后面文章将逐步介绍使用非常规深度学习方法的“图神经网络”方法做多元时间序列预测。
本节基于论文:Modeling Long- and Short-Term Temporal Patterns with Deep Neural Networks 用深度神经网络建模长期和短期的时间模式
在这些实际应用中,时序数据通常涉及长期和短期模式的混合,而传统的方法,如自回归模型和高斯过程可能会失败。本模型提出了一个新的深度学习框架,即长期和短期时间序列网络(LSTNet),以解决这一开放的挑战。
LSTNet使用卷积神经网络(CNN)来提取变量之间的短期局部关系依赖模式,使用递归神经网络(RNN)发现时间序列趋势的长期模式。此外,本模型利用传统的自回归模型来解决神经网络模型的尺度不敏感问题。
1. 问题定义
本文正式对多变量时间序列预测进行定义,给定一组观测到的时间序列信号: Y = y 1 , y 2 , . . . , y T Y={y_1,y_2,...,y_T} Y=y1,y2,...,yT,其中, y t ∈ R n y_t \in{R^n} yt∈Rn, n n n 是多元时间序列的变量维度,任务的目标是预测这组变量的未来值 y T + h y_{T+h} yT+h,其中 h h h 是预测步数。此时,在时间戳 T T T 处的输入矩阵是 X T = [ y 1 , y 2 , . . . , y T ] ∈ R n × T X_T=[y_1,y_2,...,y_T]\in{R^{n \times T}} XT=[y1,y2,...,yT]∈Rn×T。
2. 模型解读
本模型具有卷积组件、递归组件、递归-跳过层、时间注意层、自回归组件这五大模块。
2.1 卷积组件
该组件是一个没有池化的卷积网络,它旨在提取时间维度上的短期模式以及变量之间的局部依赖关系。卷积层由多个宽度为 w w w、高度为 n n n的滤波器(卷积核)组成。该组件在整个模型中的位置如下图(蓝框内)所示:

其中,第 k k k 个滤波器的输出为:
h k = R E L U ( W k ∗ X + b k ) h_k=RELU(W_k \ast X + b_k) hk=RELU(Wk∗X+bk)
其中, ∗ \ast ∗ 指卷积操作, h k h_k hk 是一个向量。多个不同的卷积核经过卷积操作后得到多组不同的向量,这组成了蓝框内右侧的卷积层输出矩阵。
2.2 递归组件
递归组件就是一个门控循环单元(GRU),使用RELU函数作为隐藏状态的更新激活函数。目的是将卷积层提取出的具有时间排列顺序的特征,通过GRU提取其时序特征。该组件在整个模型中的位置如下图(蓝框内)所示:

t t t时刻循环单元的隐藏状态计算为:
r t = σ ( x t W x r + h t − 1 W h r + b r ) u t = σ ( x t W x u + h t − 1 W h u + b u ) c t = R E L U ( x t W x c + r t ) ⊙ ( h t − 1 W h c ) + b c ) h t = ( 1 − u t ) ⊙ h t − 1 + u t ⊙ c t \begin{aligned} r_t &= \sigma(x_tW_{xr}+h_{t-1}W_{hr}+br) \\ u_t &= \sigma(x_tW_{xu}+h_{t-1}W_{hu}+bu) \\ c_t &= RELU(x_tW_{xc}+r_t) \odot (h_{t-1}W_{hc}) +b_c) \\ h_t &= (1-u_t) \odot h_{t-1}+u_t \odot c_t \end{aligned} rtutctht=σ(xtWxr+ht−1Whr+br)=σ(xtWxu+ht−1Whu+bu)=RELU(xtWxc+rt)⊙(ht−1Whc)+bc)=(1−ut)⊙ht−1+ut⊙ct
其中, ⊙ \odot ⊙ 是矩阵元素乘, σ \sigma σ 是激活函数, x t x_t xt 是本层的输入,也是卷积层输出矩阵对应在时间戳 t t t 的向量。本层的输出是多元时间序列经过卷积后在每个时间戳处的隐藏状态。
2.3 递归-跳过层
传统的GRU难以捕捉长期模式,于是可以使用跳过连接层,即通过间隔采样的方式,在采样序列长度不变的情况下,可以回看更长的时间,以此来捕获长期特征。该组件在整个模型中的位置如下图(蓝框内)所示:
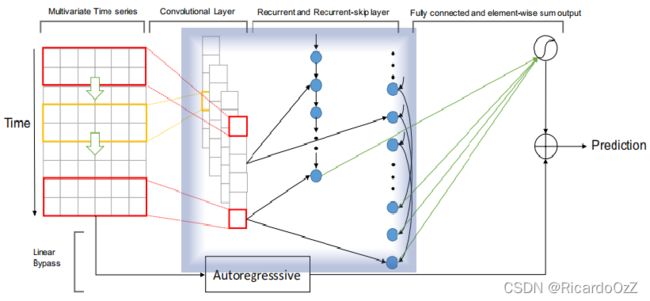
该模块依然使用GRU模型,具体更新过程如下:
r t = σ ( x t W x r + h t − p W h r + b r ) u t = σ ( x t W x u + h t − p W h u + b u ) c t = R E L U ( x t W x c + r t ) ⊙ ( h t − p W h c ) + b c ) h t = ( 1 − u t ) ⊙ h t − p + u t ⊙ c t \begin{aligned} r_t &= \sigma(x_tW_{xr}+h_{t-p}W_{hr}+br) \\ u_t &= \sigma(x_tW_{xu}+h_{t-p}W_{hu}+bu) \\ c_t &= RELU(x_tW_{xc}+r_t) \odot (h_{t-p}W_{hc}) +b_c) \\ h_t &= (1-u_t) \odot h_{t-p}+u_t \odot c_t \end{aligned} rtutctht=σ(xtWxr+ht−pWhr+br)=σ(xtWxu+ht−pWhu+bu)=RELU(xtWxc+rt)⊙(ht−pWhc)+bc)=(1−ut)⊙ht−p+ut⊙ct
其中, p p p 是间隔采样的时间长度。一般来说, p p p 的具体值要根据实验数据特性来做相应调整。
之后,可以再通过一个全连接层将递归组件和递归-跳过组件的输出组合起来。该组件在整个模型中的位置如下图(蓝框内)所示:
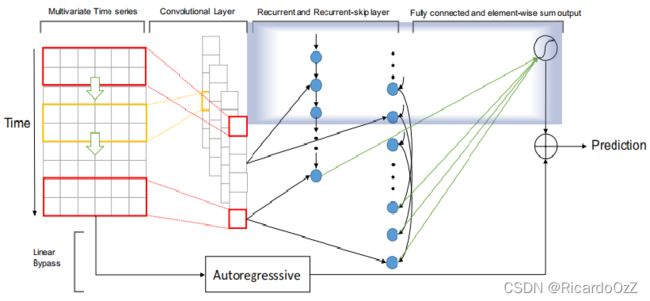
全连接层的输入包括时间戳 t t t 的递归组件隐藏状态 h t R h^R_t htR,以及递归-跳过组件的从时间戳 t − p + 1 t−p+1 t−p+1 到 t t t 的 p p p 个隐藏状态 h t − p + 1 S , h t − p + 2 S , . . . , h t S h^S_{t-p+1},h^S_{t-p+2},...,h^S_{t} ht−p+1S,ht−p+2S,...,htS。全连接层的输出计算为:
h t D = W R h t R + ∑ i = 0 p − 1 W i S h t − i S + b h^D_t=W^Rh^R_t+\sum^{p-1}_{i=0}W^S_ih^S_{t-i}+b htD=WRhtR+i=0∑p−1WiSht−iS+b
2.4 时间注意力层
然而,递归-跳过层需要一个预定义的超参数 p p p,这在非周期性或者周期长度随时间动态变化的时间序列中是不利的。为了缓解这一问题,本模型考虑了另一种方法,即注意力机制。它学习在输入矩阵的每个窗口位置的隐藏表示的加权组合。具体地说,在当前时间戳 t t t 处的注意力权重 α t ∈ R q \alpha_t \in{R^q} αt∈Rq 为:
α t = A t t n S c o r e ( H t R , h t − 1 R ) \alpha_t = AttnScore(H^R_t,h^R_{t-1}) αt=AttnScore(HtR,ht−1R)
其中, H t R , = [ h t − q R , . . . , h t − 1 R ] H^R_t,=[h^R_{t-q},...,h^R_{t-1}] HtR,=[ht−qR,...,ht−1R] 是GRU隐藏特征向量的拼接。 A t t n S c o r e AttnScore AttnScore是用于计算注意力的相似性函数,如点积、余弦相似度,或一个简单的多层感知器。
时间注意层的最终输出是将加权上下文向量 c t = H t α t c_t=H_t\alpha_t ct=Htαt和最后一个隐藏状态 h t − 1 R h^R_{t-1} ht−1R相拼接,再进行一次线性变换:
h t D = W [ c t ; h t − 1 R ] + b h^D_t=W[c_t; h^R_{t-1}]+b htD=W[ct;ht−1R]+b
2.5 自回归组件
由于卷积组件和递归组件的非线性性质,神经网络模型的一个主要缺点是输出的规模对输入的规模不敏感。
不幸的是,在特定的真实数据集中,输入信号的规模以非周期的方式不断变化,这大大降低了神经网络模型的预测精度。
我们可以考虑将LSTNet的最终预测分解为一个线性部分和一个非线性部分,其中线性部分主要关注局部规模问题,而非线性部分关注递归模式。
在LSTNet架构中,作者采用了经典的自回归(AR)模型作为线性分量。AR模型的表述如下:
h t , i L = ∑ k = 0 q a r − 1 W k a r y t − k , i + b a r h^L_{t,i}=\sum^{q^{ar}-1}_{k=0}W^{ar}_ky_{t-k,i}+b^ar ht,iL=k=0∑qar−1Wkaryt−k,i+bar
本质上,也就是一种线性层。
最后,将对神经网络部分的输出与AR分量相加,得到LSTNet的最终预测:
Y ^ t = h t D + h t L \hat{Y}_t=h^D_t+h^L_t Y^t=htD+htL