机器学习（周志华）——对数几率回归

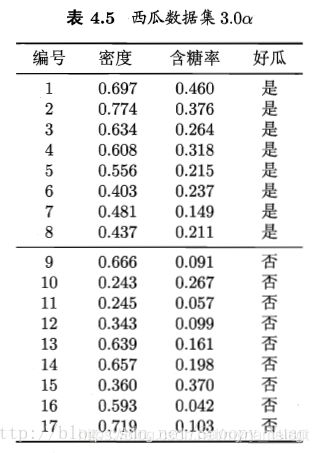
课后习题3.3,编程实现对率回归，并给出西瓜数据集3.0$a$上的结果

由公式（3.23）、（3.29）、（3.30）、（3.31）进行公式带入，

实现matlab的算法如下：

clear;clc
tic
%初始数据集
x=[0.697 0.460
    0.774 0.376
    0.634 0.264
    0.608 0.318
    0.556 0.215
    0.403 0.237
    0.481 0.149
    0.437 0.211
    0.666 0.091
    0.243 0.267
    0.245 0.057
    0.343 0.099
    0.639 0.161
    0.657 0.198
    0.360 0.370
    0.593 0.042
    0.719 0.103];
y=[1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0]';

%%对率回归的实现
%前期数据处理
x=[x ones(length(x),1)];
beta=ones(1,size(x,2));   %设定beta的初始值
n=1000;                  %设定迭代次数
%算法实现
for k=1:n
    B1=0;
    for i=1:length(x)
        B1=B1-x(i,:)*(y(i)-func_sigmod(beta,x(i,:)));
    end
    B2=0;
    for i=1:length(x)
        B2=B2+sum(x(i,:).^2)*func_sigmod(beta,x(i,:))*(1-func_sigmod(beta,x(i,:)));
    end
    beta=beta-1/B2*B1;
end
beta
toc

function y=func_sigmod(beta,x0)
y=exp(sum(beta.*x0))/(1+exp(sum(beta.*x0)));
end

Python代码实现效果如下：

import numpy as np
import math

x=np.array([[0.697,0.460],[0.774,0.376],[0.634,0.264],[0.608,0.318],[0.556,0.215],[0.403,0.237],[0.481,0.149],[0.437,0.211],[0.666,0.091],
            [0.243,0.267],[0.245,0.057],[0.343,0.099],[0.639,0.161],[0.657,0.198],[0.360,0.370],[0.591,0.042],[0.719,0.103]])
y=np.array([1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0])

##对率回归的实现

#前期数据处理
ones1=np.array([[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]])
ones1=ones1.T
x1=np.concatenate((x,ones1),axis=1)
beta=np.array([1,1,1])    #设定beta的初始值
n=1000;                   #设定迭代次数

def func_sigmod(beta,x0):
    y = math.exp(np.dot(beta,x0))/(1+math.exp(np.dot(beta,x0)))
    return y

#算法实现
for k in range(0,n):
    B1=0
    for j in range(len(x)):
        B1=B1-x1[j,:]*(y[j]-func_sigmod(beta,x1[j,:]))
    B2=0
    for j in range(len(x)):
        B2=B2+(x1[j,:]**2).sum()*func_sigmod(beta,x1[j,:])*(1-func_sigmod(beta,x1[j,:]))
    beta=beta-1/B2*B1
print(beta)