(AGC)Attributed Graph Clustering via Adaptive Graph Convolution

本文提出了一种自适应图卷积方法(AGC)，该方法利用高阶图卷积来捕获全局的社区结构，并自适应地为不同的图选择合适的顺序。

• AGC是从图信号处理谱图理论的角度来理解GNN并增强了聚类效果
• AGC可以自适应的选择高阶信息的阶数

AGC包括两个步骤:

1. 进行k阶图卷积，获得平滑的特征表示;
2. 对学习到的特征进行谱聚类，对节点进行聚类。

AGC可以很容易地使用高阶图卷积来捕获全局社区结构，并可以为不同的图选择合适的k值。

图卷积：

图信号可以被表示为向量$f=[f(v_1),...,f(v_n)]$,其中$f:V⟶\mathbb{R}$是节点上的实值函数。

给定邻接矩阵A，顶点度矩阵D$(D=diag(d_1,...,d_n))$，那么拉普拉斯矩阵L = D - A。

对称归一化的拉普拉斯算子为：$L_s=I-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$.可以被特征分解为:$L_S=U\Lambda U^{-1}$.$\Lambda =diag({\lambda }_1,...,{\lambda }_n)$是按递增次序排列的特征值，U是相关的正交特征向量。

线形图过滤器可以表示为一个矩阵：$$G=Up(\Lambda )U^{-1}\in {\mathbb{R}}^{n\times n}$$,其中$p(\Lambda )=diag(p({\lambda }_1),...,p({\lambda }_n))$被称为G的频率响应函数，可以对特征值进行放缩。

图卷积定义为图信号f与图滤波器G的乘积：$\overline{f}=Gf$.其中$\overline{f}$是过滤后的图信号。

特征矩阵X的每一列都可以看做是一个图信号，可以将特征值${\lambda }_q$作为频率，相关联的特征向量$u_q$作为图的傅里叶基。

一个图信号可以被分解为特征向量的线性组合：$f=Uz=\sum _{q=1}^n{z}_q{u}_q$.

可以看作是一组基信号的加权，其中z为q的系数，系数的大小表示基信号$u_q$在f中的强度。所以基是由该图信号的归一化拉普拉斯算子特征分解得到($L_S=U\Lambda U^{-1}$)。

如果图上的邻近节点具有相似的特征表示，则图信号是平滑的，基信号$u_q$的平滑度可以用下式测量：
$$\begin{gathered} \Omega (u_q)=\frac{1}{2}\sum _{(v_i,v_j)\in e}{a}_{ij}\Vert \frac{u_q(i)}{{\sqrt{d}}_i}-\frac{u_q(j)}{{\sqrt{d}}_j}{\Vert }_2^2 \\ =u_q^T{L}_s{u}_q={\lambda }_q \end{gathered}$$

${\lambda }_q$的大小可以反映基向量$u_q$的平滑程度.，图上的平滑程度反应了相邻节点的相似程度。图上的高频：不平滑，特征值大。低频：平滑，特征值小。

式子说明低频(特征值越小)对应的基信号越平滑，即平滑的图信号f中低频信号应该比高频信号多。可以通过低通图滤波器G进行图卷积来实现，综合上面的公式得到：$\overline{f}=Gf=Up(\Lambda )U^{-1}\cdot U_z=\sum _{q=1}^{n}p({\lambda }_q)z_q{u}_q$.

通过前面我们知道，一组基中，相对平滑的图信号有利于聚类，为了保留图信号f中的低频基信号，去除f中的高频基信号，图滤波器G应该为低通的，即频率响应函数$p(\cdot )$为递减非负函数:$p({\lambda }_q)=1-\frac{1}{2}{\lambda }_q$.

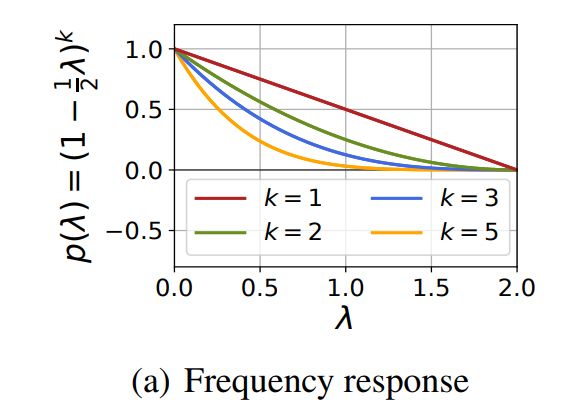
如图所示，归一化拉普拉斯Ls的特征值都属于区间[0,2]，在这个区间我们的$p(\cdot )$是递减且非负的趋势，表明它是低通的。将我们的图滤波器代入频率响应函数$p(\cdot )$：$G=Up(\Lambda )U^{-1}=U(I-\frac{1}{2}\Lambda )U^{-1}=I-\frac{1}{2}{L}_S$.

通过对特征矩阵X进行图卷积，得到过滤后的特征矩阵：$\overline{X}=GX=(I-\frac{1}{2}{L}_s)X$.

为了便于聚类，在图过滤后，希望同一类的节点具有相似的特征表示。但是，上式的一阶图卷积可能不足以实现这一点，特别是对于大型稀疏的图，因为它仅通过其1跳邻居的聚合来更新每个节点，而不考虑长距离的领域关系。为了捕获全图结构并便于聚类，提出了K阶图卷积：$\overline{X}=(I-\frac{1}{2}{L}_s{)}^{k}X$.

其中k是正整数，对应的图过滤器是：$G=(I-\frac{1}{2}{L}_S{)}^k=U(I-\frac{1}{2}\Lambda {)}^k{U}^{-1}$,频率响应函数为：$p({\lambda }_q)=(1-\frac{1}{2}{\lambda }_q{)}^k$.由上面的图片可以看出随着k的增加，$p({\lambda }_q)$变得更低，表明过滤后的节点特征X将更平滑。

前面我们得到$\overline{X}=(I-\frac{1}{2}{L}_s{)}^{k}X$代入$L_s=I-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$,Ls矩阵的第i行将与X相乘得到对应的$x_i$,
所以$x_i$的计算公式：
$$\begin{gathered} \overline{X}=(I-\frac{1}{2}{L}_s)X=\frac{1}{2}(I+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}})X \\ 其中\overline{x_i}=\frac{1}{2}(x_i+\sum _{(v_i,v_j)\in e}\frac{a_{ij}}{\sqrt{d_i{d}_j}}{x}_j) \end{gathered}$$
K阶图卷积的计算公式如下：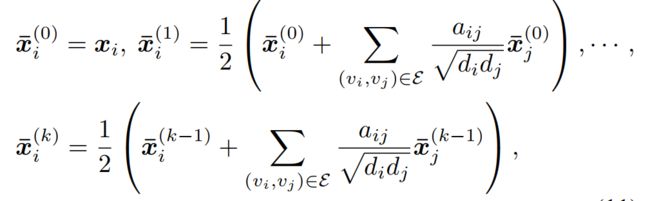
通过自适应图卷积聚类

本文使用经典的谱聚类方法，利用过滤后的特征矩阵$\overline{X}$将节点划分为m个社区。

首先应用线性核$K=\overline{X}{\overline{X}}^T$来学习节点之间的两两相似度，然后计算$W=\frac{1}{2}(|K|+|K^T|)$来确保相似度矩阵是对称非负的。最后，对W进行谱聚类，通过计算与W的m个最大特征值关联的特征向量。然后对特征向量应用K-means算法，得到聚类结果。

K阶图卷积的核心问题是如何选择一个合适的k。虽然k阶图卷积可以使邻近的节点具有相似的特征表示。但k不是越大越好，k过大会导致过平滑，即不同簇中节点的特征混合，变得难以区分。下图可以看出，随着k的增加，节点特征趋于相似。K= 12时数据显示出清晰的聚类结构。在k = 100的情况下，特征过平滑，将来自不同集群的节点混合在一起。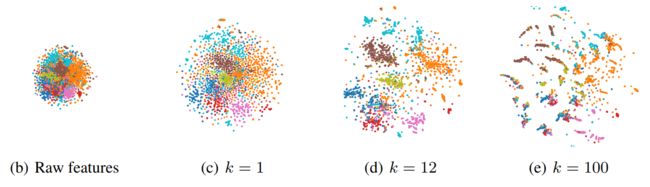
为了自适应选择阶数k，使用基于数据本身固有信息的聚类性能度量内部标准，在这里，使用的是给定划分的社区内距离$intra(C)$，他表示划分的紧凑性。

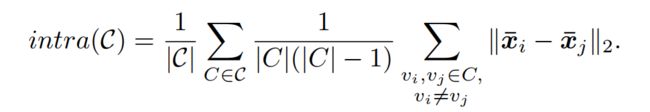
需要注意的是，社区间距离也可以用来衡量聚类性能，一个好的社区划分应该具有较大的社区间距离和较小的社区内距离。但是随着k的增加，特征变得更加平滑，将导致社区内和社区间的距离显著下降，此时，社区间距离可能不再可靠。

该方法的策略是找到社区内距离的第一个局部最小值(不断使k加1的迭代，直到社区内距离不再减少)。

AGC算法：

• 输入：节点集V，邻接矩阵A，特征矩阵X，最大迭代数max_iter
• 输出：社区划分C。
• 1：初始化$t=0,intra(C^{(0)})=+\infty$. 计算对称归一化的拉普拉斯算子$L_S=I-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$.
• 2：循环
• 3： 令t = t+1, k = t.
• 4： 根据公式进行k阶图卷积，得到$\overline{X}$.
• 5： 应用线性核 $K=\overline{X}{\overline{X}}^T$, 并计算相似度矩阵$W=\frac{1}{2}(|K|+|K^T|)$.
• 6： 对W执行谱聚类，得到社区划分$C^{(t)}$.
• 7： 根据公式计算$intra(C^{(t)})$.
• 8：直到$.d\_intra(t-1)>0ort>max\_iter$.其中($d\_intra(t-1)=intra(C^{(t)})-intra(C^{(t-1)})$ ).
• 9：设置$k=t-1,C=C^{(t-1)}$.

代码如下

import scipy.io as sio
import time
import numpy as np
import scipy.sparse as sp
from sklearn.cluster import KMeans
from metrics import clustering_metrics


def Graph_Clustering(adj, loop=True):
    # 通过公式计算图卷积G
    if loop:
        adj = adj + sp.eye(adj.shape[0])

    # sp.coo_matrix生产矩阵
    adj = sp.coo_matrix(adj)
    # 计算行和 即为每个节点的度
    rowsum = np.array(adj.sum(1))
    d_inv_sqrt = np.power(rowsum, -0.5).flatten()
    # 将无穷大位置置为0
    d_inv_sqrt[np.isinf(d_inv_sqrt)] = 0.
    # 对矩阵进行对角化
    d_mat_inv_sqrt = sp.diags(d_inv_sqrt)
    # Coordinate list (COO) 其思想是 按照(row_index, column_index, value)的方式存储每一个非0元素
    temp = d_mat_inv_sqrt.dot(adj).dot(d_mat_inv_sqrt).tocoo()
    # 代入公式计算G
    return (sp.eye(temp.shape[0]) + temp)/2


def to_onehot(prelabel):
    # 将标签转换为独热编码 eg. 假如有6类，标签不再是3而变成[0,0,1,0,0,0]
    k = len(np.unique(prelabel))
    label = np.zeros([prelabel.shape[0], k])
    # 将标签对应序号变为1
    label[range(prelabel.shape[0]), prelabel] = 1
    label = label.T
    return label


def intra_dist(prelabel, feature):
    # 计算社区内距离
    if sp.issparse(feature):
        feature = feature.todense()
    feature = np.array(feature)

    onehot = to_onehot(prelabel)

    m, n = onehot.shape
    # 统计每一类(社区)有多少节点
    count = onehot.sum(1).reshape(m, 1)
    # 数量做分母 防止溢出  将0置为1
    count[count == 0] = 1

    # 在每一行中，与有相同标签相关联的节点特征的平均值
    mean = onehot.dot(feature) / count
    # 对标签求和(平均向量的平方特征)
    a2 = (onehot.dot(feature * feature) / count).sum(1)
    # 距离
    pdist2 = np.array(a2 + a2.T - 2 * mean.dot(mean.T))

    # 不同标签之间的距离
    intra_dist = pdist2.trace()
    inter_dist = pdist2.sum() - intra_dist
    intra_dist /= m
    inter_dist /= m * (m - 1)
    return intra_dist