粗糙集相关概念及理论分析总结(一)
粗糙集
概念:粗糙集理论(Rough Set Theory,简称RST)是一种不需要提供数据之外的任何先验信息来处理不完备、不确定信息的数学工具。其最早的提出是由波兰学者Pawlak于1982年首次提出,其主要思想是利用已知的信息或者知识来近似刻画不精确或者不确定的目标概念
为了规范化,我们认为空集也是一个概念,称为空概念。为了规范化,我们认为空集也是一个概念,称为空概念。论域U中的任何子集簇(概念簇)称为关于U的抽象知识,简称知识。论域中的每一个概念(子集)表示他的一个信息粒。论域中的每一个概念(子集)表示他的一个信息粒
粗糙集基础
在粗糙集理论中,特征选择的研究对象主要以符号型取值的数据为主,表示为一个信息系统,它可以表示为一个四元组S=(U,A,V,f),其中U为非空有限对象集合,也称为论域,A为非空有限特征集合,Va∈A,Va表示特征a的值域;f:为U×A→V 是一个信息函数,∀x∈U,a∈A,定义f(x,a)表示x在特征a上的取值,则有f(x,a)∈Va。如果A=C∪D,且C∩D=∅,其中C为条件特征集合,D为决策特征集合,则信息系统被称为决策系统。
相关领域内的不同名称 :从数学角度看,粗糙集是研究集合的,人工智能角度而言,粗糙集研究的是决策表,而对于编程而言,则是一些特殊的矩阵。
主要思想 在保持分类能力不变的前提下,通过知识约简,导出问题的决策或分类规则。
概念举例子
| 病人 | 头疼 | 肌肉 | 体温 | 流感 |
|---|---|---|---|---|
| e1 | 是 | 是 | 正常 | 否 |
| e2 | 是 | 是 | 高 | 是 |
| e3 | 是 | 是 | 很高 | 是 |
| e4 | 否 | 是 | 正常 | 否 |
| e5 | 否 | 否 | 高 | 否 |
| e6 | 否 | 是 | 很高 | 是 |
相关概念整理 抽象概念具体化
如:U为论域,即为非空有限对象的集合。则U对应的为 U={e1,e2,e3,e4,e5,e6},除第一列以外,其他类则为属性,其中分为条件属性和决策属性,此案例中,最后一列则为决策属性,有些文献中 决策系统 表示为
DS=(U,A=C∪D,V,f) ,例如头疼属性则为C1,其集合表现形式则为C1={是,是,是,否,否,否},决策属性D1={否,是,是,否,是是},若决策属性只有一个,则为单决策系统,若为两个及以上,则为多决策系统。
等价类和等价关系
等价关系的定义
定义: 若R为非空集合A上的关系,则R是自反的、对称的和传递的,则称R为A上的等价关系,对于任意的x,y ∈A,若
举例说明 :(1)如果说X是汽车的集合,∼是汽车颜色相同的等价类,则一个特定等价类由所有的绿色汽车组成。X/∼自然被认为所有汽车颜色的集合。
(2)考虑到整数集合Z上的 “模2” 等价关系,x∼y当且仅当x−y是偶数。这个关系精确地引发两个等价类:[0]由所有的偶数组成,[1]由所有的奇数组成。在这种关系下,[7],[9]和[1]都表示Z/∼的同一个元素。
在简要了解等价类这个概念后,下面我们将给出粗糙集中的等价类和等价关系:
S=(U,A=C∪D,V,f)是决策信息系统,∀B⊆C,论域U的不可分辨关系被定义为:
RB={(x,y)∈U×U|f(x,a)=f(y,a),∀a∈B}
很显然,不可分辨关系是一种等价关系。它将论域U划分为U/RB,U/RB={E1,E2,…,Em}是由等价关系RB形成的等价类集合。由等价关系RB形成的等价类[x]B={y|(x,y)∈RB}是粗糙集理论中的基本知识粒。
继续以病人决策表为相关例子
设论域U={e1,e2,e3,e4,e5,e6},条件属性C={C1,C2,C3},决策属性D={d}。 C1为头疼,C2为肌肉疼,C3为体温,有三个条件属性。
先来看头疼这个条件属性C1,它的值域只有两个:“是”和“否”。
U/{C1}={{e1,e2,e3},{e4,e5,e6}}={{是},{否}}
{e1,e2,e3}为“是”
{e4,e5,e6}为“否”
C1为论域U上一个知识
再看肌肉疼这个条件属性C2,它的值域只有两个:“是”和“否”。
U/{C2}={{e1,e2,e3,e4,e6},{e5}}={{是},{否}}
{e1,e2,e3,e4,e6}为“是”
{e5}为“否”
C2为论域U上一个知识
等价类 :等价类:设R是集合A上的等价关系,与A中的一个元素a有关系的所有元素的集合叫做a的等价类
精确集和粗糙集的区别
以体温C3这个条件属性为例
U/C3={{e1,e4},{e2,e5},{e3,e6}}={X1,X2,X3}
如果X={e1,e2,e4,e5}。
那么X=X1∪X2={e1,e4}∪{e2,e5}
X可以由已有的X1,X2,X3中的若干个{X1,X2}组成,因此X是C3精确集
如果X={e1,e2,e4}
则X={e1,e4}∪{e2}
此时,X不能用X1,X2,X3中的任何一个或者若干个组合构成,那么X是C3粗糙集
上近似、下近似、等相关理论分析
对于任意的子集x∈u,x不一定能用Q中的知识精确地描述,这时需用两个近似集下近似和上近似来表示
| 病人 | 体温 |
|---|---|
| e1 | 正常 |
| e2 | 高 |
| e3 | 很高 |
| e4 | 正常 |
| e5 | 高 |
| e6 | 很高 |
在这个信息系统中 S=(U,C),其中U为论域,C={c3},c3是体温这个属性。
U/C={{e3,e6},{e2,e5},{e1,e4}}={X1,X2,X3}
若给定一个集合,X={e1,e2,e4},显然X是C的粗糙集,因为X不能被X1,X2,X3中的任何一个或者若干个组合构成。
此处的上近似看一下如何从决策系统中表示
{e3,e6}⋂X=∅⟹X1⋂X=∅
{e2,e5}⋂X={e2}⟹X2⋂X={e2}
{e1,e4}⋂X={e1,e4}⟹X3⋂X={e1,e4}
此时,称{e2,e5}和{e1,e4}为X关于C的上近似。且如下图所示 R(x) 上划线 表示其上近似区域,其区域与原先的形状相比,明显要比原来形状要大
下面阐述一下下近似
在U/C={X1,X2,X3}中,
{e3,e6}⊈X⟹X1⊈X
{e2,e5}⊈X⟹X2⊈X
而{e1,e4}⊆X⟹X3⊆X
此时,称{e1,e4}为X关于C的下近似。
就图形表示而言,下近似区域明显小于原区域
给出上下近似的定义:
在一个决策信息系统中S=(U,A=C⋃D,V,f)中,R是一个等价关系,∀X⊆U,X关于R的上近似和下近似的定义分别如下:
R¯X=⋃{x∈U∣[x]R⊆X}
R_X=⋃{x∈U∣[x]R⋂X≠∅}
[x]B={y∣(x,y)∈RB}表示是由等价关系RB形成的等价类。
通俗而言: 上近似则是将那些包含X的知识库中的集合求并得到的(包含X的最小可定义集),下近似则是那些所有的包含于X的知识库中的集合中求并得到的(包含在X内的最大可定义集)
或者说:
上近似是根据现有的知识R,判断U中一定属于和可能属于X对象所组成的集合
下近似则是判断U中所有肯定属于X的对象所组成的集合。
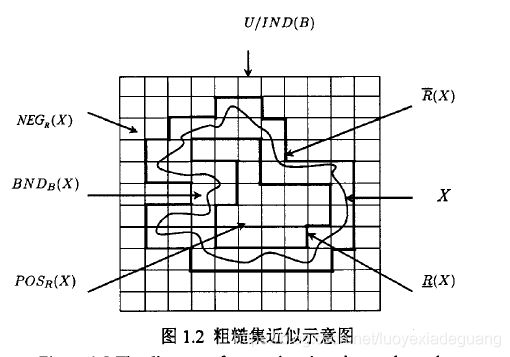
正负区域和边界域的关系
正区域: POSR(X)=R_(X) :即正区域等于下近似
负区域: NEGR(X)=U−R¯(X):即全集减去上近似
边界域: BNDR(X)=R¯(X)- R_(X):即上近似减去下近似
其满足以下性质,即
正区域∪负区域∪边界域=U(全集U)
![]()
举例子:

其中论域U={1,2,3,4,5,6,7,8,9},条件属性集C={a,b,c,f,e},决策属性集 D={d}。从上表中有:U={x1,x2,x3,x4,x5,x6,x7,x8,x9},C={a,b,c,f,e},D={d}。每个属性的值域都为{0,1}。
由上图可以得到
U/C={{1},{2,4},{3,5},{6,7},{8,9}}={U1,U2,U3,U4,U5},注意此处的C表示条件属性,其划分的依据在于U在各条件特征的值相同,如,病人2和病人4的决策特征是相同的。此处不涉及到决策特征d
假设X={1,2,3,6,7}
则 其
上近似为:R¯(X)=U1∪U2∪U3∪U4={1,2,4,3,5,6,7}
下近似 为:R_(x)={1,6,7}
正区域 为 : POSR(X)=R_(X)={1,6,7}
负区域 为: NEGR(X)=U−R¯(X)={8,9}
边界域 为:R¯(X)-- R_(X)={2,3,4,5}
本文部分引用来自:
(1) 面向动态不完备数据的特征选择模型与算法研究[D].北京交通大学,2015.
(2)相关博客链接 https://www.cnblogs.com/Gedanke/p/12357261.html
