深度学习中常用激活函数分析

0. 引言

0.1 什么是激活函数，有什么作用

激活函数是向神经网络中引入非线性因素，通过激活函数神经网络就可以拟合各种曲线。激活函数主要分为：

• 饱和激活函数（Saturated Neurons）
• 非饱和函数（One-sided Saturations）

经典的Sigmoid和Tanh就是典型的饱和激活函数，而ReLU以及其变体为非饱和激活函数。

非饱和激活函数对比饱和激活函数主要有如下优势：

1. 可以解决/抑制梯度消失问题
2. 可以加速收敛

1. 典型的饱和激活函数 —— Sigmoid & Tanh

1.1 Sigmoid激活函数

Sigmoid激活函数及其导函数定义如下：

$$S(x)=\frac{1}{1+e^{-x}}$$
$$S^{\prime }(x)=\frac{e^{-x}}{(1+e^{-x}{)}^2}=S(x)(1-S(x))$$

Sigmoid的函数图像和Sigmoid的梯度函数图像分别为下图所示。

从图像可以看出，函数两个边缘的梯度约为$0$，梯度的取值范围为 $(0,0.25)$。这就导致：

1. Sigmoid极容易导致梯度消失问题。饱和神经元会使得梯度消失问题雪上加霜，假设神经元输入Sigmoid的值特别大或特别小，对应的梯度约等于0，即使从上一步传导来的梯度较大，该神经元权重(w)和偏置(bias)的梯度也会趋近于0，导致参数无法得到有效更新。
2. 计算费时。 在神经网络训练中，常常要计算Sigmid的值进行幂计算会导致耗时增加。
3. Sigmoid函数不是关于原点中心对称的（zero-centered)。

1.1 Tanh激活函数

Tanh激活函数及其导函数定义如下：

$$\begin{array}{rl}\tanh (x)& =\frac{\sinh (x)}{\cosh (x)}\\ & =\frac{e^x-e^{-x}}{e^x+e^{-x}}\end{array}$$
$${\tanh }^{\prime }(x)=1-{\tanh }^2(x)$$

Tanh的函数图像和Tanh的梯度函数图像分别为下图所示。

优点：

1. 解决了sigmoid函数收敛变慢的问题，相对于Sigmoid提高了收敛速度。
2. 因为Tanh和Sigmoid的导函数有上下界，所以完全不用担心因为使用激活函数而产生梯度爆炸的问题
3. Tanh激活函数解决了原点中心对称问题。

缺点：
4. 指数的计算复杂。
5. 梯度消失的问题依旧保留，因为两边的饱和性使得梯度消失，进而难以训练。

2. 单侧饱和的激活函数 —— ReLU

ReLU激活函数及其导函数定义如下：

$$\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}(x)=\{\begin{array}{ll}x,& x\ge 0\\ 0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}$$
$${\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}}^{\prime }(x)=\{\begin{array}{ll}1,& x\ge 0\\ 0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}$$

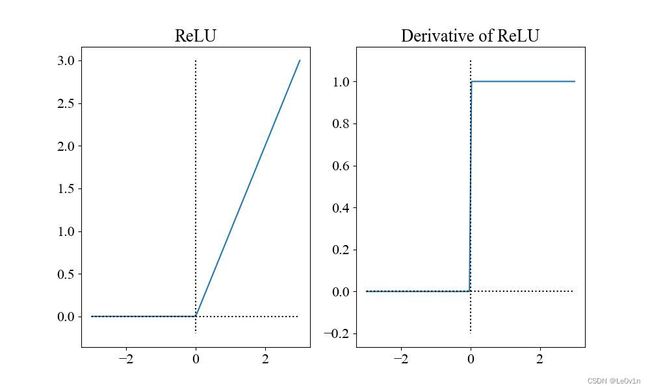
ReLU的函数图像和ReLU的梯度函数图像分别为下图所示。

根据函数图像我们首先就可以看到，即便输入很大，ReLU也可以让梯度正常的回传，因此ReLU解决梯度消失问题。

2.1 ReLU的优势

ReLU激活函数的提出就是为了解决梯度消失问题。ReLU的梯度只可以取两个值：0或1。

• 当输入小于0时，梯度为0
• 当输入大于0时，梯度为1

这样的好处就是：ReLU的梯度的连乘不会收敛到0，连乘的结果也只可以取两个值：0或1 。

• 如果值为1，梯度保持值不变进行前向传播
• 如果值为0 ,梯度从该位置停止前向传播

Sigmoid函数是双侧饱和的，即朝着正负两个方向函数值都会饱和；但ReLU函数是单侧饱和的，即只有朝着负方向，函数值才会饱和。严格意义上来说，将ReLU函数值为0的部分称作饱和是不正确的(饱和应该是取值趋近于0)，但效果和饱和是一样的。

---

假设神经元为检测某种特定特征的开关，高层神经元负责检测高级的/抽象的特征(有着更丰富的语义信息)，例如眼睛或者轮胎；低层神经元负责检测低级的/具象的特征(曲线或者边缘)。

当开关处于开启状态，说明在输入范围内检测到了对应的特征，且正值越大代表特征越明显。加入某个神经元负责检测边缘，则正值越大代表边缘区分越明显(sharp)。

假设一个负责检测边缘的神经元，激活值为1相对于激活值为0.5来说，检测到的边缘区分地更明显；但激活值-1相对于-0.5来说就没有意义了，因为低于0的激活值都代表没有检测到边缘。所以用一个常量值0来表示检测不到特征是更为合理的，像ReLU这样单侧饱和的神经元就满足要求。

---

单侧饱和还能使得神经元对于噪声干扰更具鲁棒性。假设一个双侧都不饱和的神经元，正侧的不饱和导致神经元正值的取值各不相同，这是所希望的，因为正值的大小代表了检测特征信号的强弱。但负值的大小引入了背景噪声或者其他特征信息，这会给后续的神经元带来无用的干扰且可能导致神经元之间的相关性，相关性是容易造成模型病态的。

例如检测直线的神经元和检测曲线的神经元可能有负相关性。在负值区域单侧饱和的神经元则不会有上述问题，噪声的程度大小被饱和区域都截断为0，避免了无用信息的干扰。

---

使用ReLU激活函数在计算上也是高效的。相对于Sigmoid函数梯度的计算，ReLU函数梯度取值只有0或1。且ReLU将负值截断为0 ，为网络引入了稀疏性，进一步提升了计算高效性。

2.2 ReLU的缺点 —— 神经元死亡

ReLU最大的缺点便是会导致部分神经元死亡。ReLU带来的稀疏性尽管可以提升计算高效性，但同样也可能阻碍训练过程。

通常，激活函数的输入值有一偏置项(bias)，假设bias变得太小，以至于输入激活函数的值总是负的，那么反向传播过程经过该处的梯度恒为0,对应的权重和偏置参数此次无法得到更新。如果对于所有的样本输入，该激活函数的输入都是负的，那么该神经元再也无法学习，称为神经元死亡问题。

2.3 ReLU总结

优点：—— 与 Sigmoid和Tanh激活函数相比

1. 解决梯度消失问题
2. 作为单侧饱和的激活函数，其特性非常符合神经元的工作原理
3. 将神经元负值置0（负值截断特性），增强神经元对噪声的鲁棒性
4. 为网络带来稀疏性 —— 相当于正则项，将模型部分简化
5. 计算简单，计算高效，可以提升网络的推理速度

缺点：

1. 因为负值阶段特性，会导致部分神经元死亡，无法反向传播

3. ReLU变体 — Leaky ReLU

为解决ReLU带来的神经元死亡问题，引入Leaky ReLU。

3.1 函数及其导函数

$$\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{y}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}=\{\begin{array}{ll}x,& x>0\\ \alpha x,& x\le 0\end{array}$$
$${\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{y}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}}^{\prime }=\{\begin{array}{ll}1,& x>0\\ -\alpha ,& x\le 0\end{array}$$

$\alpha$默认为$0.01$，Leaky ReLU及其导函数图像：

3.2 Leaky ReLU的优点

Leaky ReLU的提出就是为了解决神经元”死亡“问题，Leaky ReLU与ReLU很相似，仅在输入小于0的部分有差别，ReLU输入小于0的部分值都为0，而LeakyReLU输入小于0的部分，值为负，且有微小的梯度。

使用Leaky ReLU的好处就是：在反向传播过程中，对于Leaky ReLU激活函数输入小于零的部分，也可以计算得到梯度(而不是像ReLU一样值为0)，这样就避免了梯度方向锯齿问题。

3.3 不同$\alpha$的Leaky ReLU激活函数图像

3.4 随机Leaky ReLU

$\alpha$ 的分布满足均值为0，标准差为1的正态分布，该方法叫做随机Leaky ReLU(Randomized Leaky ReLU)。

原论文指出随机Leaky ReLU相比Leaky ReLU能得更好的结果，且给出了参数 $\alpha$ 的经验值 —— $\frac{1}{5.5}$ (好于0.01)。

至于为什么随机Leaky ReLU能取得更好的结果，解释之一就是：随机Leaky ReLU小于0部分的随机梯度，为优化方法引入了随机性，这些随机噪声可以帮助参数取值跳出局部最优和鞍点。

4. ReLU变体 — PReLU

函数及其导数定义如下：

$$\mathrm{P}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}=\{\begin{array}{ll}x,& x>0\\ \alpha x,& x\le 0\end{array}$$
$${\mathrm{P}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}}^{\prime }=\{\begin{array}{ll}1,& x>0\\ -\alpha ,& x\le 0\end{array}$$

PReLU (Parametrized ReLU)和Leaky ReLU比较相似，唯一不同是：$\alpha$并非人为设计，而是一个可学习参数。

5. ReLU变体 — ELU(Exponential Linear Unit)

5.1 理想激活函数的条件

理想的激活函数应满足两个条件：

1. 输出的分布是零均值的，可以加快训练速度。
2. 激活函数是单侧饱和的，可以更好的收敛。

• ReLU满足第2个条件，不满足第1个条件
• LeakyReLU和PReLU满足第1个条件，但不满足第2个条件

5.2 ELU及其导函数定义

两个条件都满足的激活函数为ELU(Exponential Linear Unit)，其导函数定义如下：

$$\mathrm{E}\mathrm{L}\mathrm{U}=\{\begin{array}{ll}x,& x>0\\ \alpha (e^x-1),& x\le 0\end{array}$$
$${\mathrm{E}\mathrm{L}\mathrm{U}}^{\prime }=\{\begin{array}{ll}1,& x>0\\ -\alpha e^x,& x\le 0\end{array}$$

其中，$\alpha$一般取$1$。其函数及其导函数图像如下：

可以看到：

• 当$x\ge 0$时，ELU=ReLU；
• 当$x<0$时，ELU的下限为$-\alpha$，无限趋近于$-\alpha$

5.4 ELU激活函数的优点

当激活值的均值非0时，就会对下一层造成一个bias，如果激活值之间不会相互抵消（即均值非0），会导致下一层的激活单元有bias shift。如此叠加，单元越多时，bias shift就会越大。

除了ReLU，其它激活函数都将输出的平均值接近0，从而加快模型收敛，类似于Batch Normalization的效果，但是计算复杂度更低。

虽然LeakReLU和PReLU都也有负值，但是它们不保证在不激活状态下（就是在输入为负的状态下）对噪声鲁棒。

反观ELU在输入取较小值时具有软饱和的特性，提升了对噪声的鲁棒性。

5.3 ELU激活函数的缺点

1. 使用ELU的神经网络训练和推理都会更慢一些，因为需要更复杂的指数运算得到函数激活值。

一般涉及到$e^x$的激活函数计算量都比较大。

6. ReLU变体 — SELU激活函数

6.1 函数及其导函数定义

SELU(Scaled Exponential Linear Units，缩放指数线性单元)其函数及其导函数定义如下：
$$\mathrm{S}\mathrm{E}\mathrm{L}\mathrm{U}=\lambda \{\begin{array}{ll}x,& x>0\\ \alpha e^x-\alpha ,& x\le 0\end{array}$$
$${\mathrm{S}\mathrm{E}\mathrm{L}\mathrm{U}}^{\prime }=\lambda \{\begin{array}{ll}1,& x>0\\ -\alpha e^x,& x\le 0\end{array}$$

其中：

• $a\approx 1.6732632423543772848170429916717$
• $\lambda \approx 1.0507009873554804934193349852946$

可以看到，它们的小数点后还有很多位，这是为了绝对精度。而且它们是预先确定的，也就是说我们不必担心如何为这个激活函数选取合适的 $\alpha$ 值。说实话，这个公式看起来和其它公式或多或少有些类似。所有新的激活函数看起来就像是其它已有的激活函数的组合。

---

其函数及其导函数图像如下所示：

6.2 SELU的注意事项

1. 当实际应用这个激活函数时，必须使用 lecun_normal 进行权重初始化
2. 如果希望应用 dropout，则应当使用 AlphaDropout

6.3 SELU激活函数的优点

1. 内部归一化的速度比外部归一化快，这意味着网络能更快收敛
2. 不可能出现梯度消失或爆炸问题

6.4 SELU激活函数的缺点

1. 这个激活函数相对较新——需要更多论文比较性地探索其在 CNN 和 RNN 等架构中应用。

使用19年使用 SELU 的 CNN 论文：Effectiveness of Self Normalizing Neural Networks for Text Classification
[该论文的摘要] 在前馈神经网络（FNN）上提出的自归一化神经网络（SNN）在各种机器学习任务中的表现优于常规FNN架构。特别是在计算机视觉领域，为SNNs提出的激活函数Scaled Exponential Linear Units（SELU）比其他非线性激活（如ReLU）表现得更好。SNN的目标是为正常化的输入产生一个正常化的输出。已有的神经网络架构，如前馈网络和卷积神经网络（CNN），缺乏规范化输出的内在性质。因此，需要额外的层，如批量归一化。尽管SNNs取得了成功，但它们在CNN等其他网络架构上的特征还没有被探索出来，尤其是在自然语言处理领域。在本文中，我们旨在展示拟议的自归一化卷积神经网络（SCNN）在文本分类中的有效性。我们分析了它们与标准CNN架构在几个文本分类数据集上的表现。我们的实验表明，SCNN以明显较少的参数取得了与标准CNN模型相当的结果。此外，在参数数量相同的情况下，它的性能也优于CNN。

7. ReLU变体 — GELU

高斯误差线性单元（Gaussian Error Linear Units, GELUs）激活函数在最近的 Transformer 模型（谷歌的 BERT 和 OpenAI 的 GPT-2）中得到了应用。GELU 的论文来自 2016 年，但直到最近才引起关注。

7.1 函数及其导函数定义

$$\begin{array}{rl}\mathrm{G}\mathrm{E}\mathrm{L}\mathrm{U}& =x\times \Phi (x)\\ & =0.5x\left(1+\tanh (\sqrt{\frac{2}{\pi }}(x+0.044715x^3))\right)\end{array}$$

其中 $Phi(x)$ 表示高斯分布的累积概率分布，即在 $(-\infty ,x]$ 区间对高斯分布的定积分。一般 $Phi(x)$ 常见的是均值为0，方差为1的版本。

$$\begin{array}{rl}{\mathrm{G}\mathrm{E}\mathrm{L}\mathrm{U}}^{\prime }& =0.5\tanh (0.0356774x^3+0.797885x)\\ & +(0.0535161x^3+0.398942x){\text{sech}}^2(0.0356774x^3+0.797885x)+0.5\end{array}$$
$$\begin{array}{rl}\text{sech}(x)& =\frac{1}{\text{ch}(x)}\\ & =\frac{2}{e^x+e^{-x}}\end{array}$$

当方差为无穷大，均值为0的时候，GeLU就等价于ReLU了。GELU可以当作为RELU的一种平滑策略。

其函数及其导函数图像如下：

可以看出：

• 当 x 大于 0 时，输出为 x
• 但 x=0 到 x=1 的区间除外，这时曲线更偏向于 y 轴 (y > x)
• 当 x > 1，可以近似看成是ReLU（但是GELU的实现比ReLU要复杂得多）

7.2 GELU激活函数的优点

1. 似乎是 NLP 领域的当前最佳
2. 在 Transformer 模型中表现最好
3. 能避免梯度消失问题。

7.3 GELU激活函数的缺点

1. 尽管是 2016 年提出的，但在实际应用中还是一个相当新颖的激活函数，因此工程经验没有像ReLU那么丰富
2. 计算量大，影响模型推理速度

7.4 GELU在使用中的建议

当训练过程中使用GELU作为激活函数进行训练的时候，建议使用一个带有动量(momentum)的优化器。

8. ReLU变体 — Mish激活函数

8.1 函数及其导函数定义

Mish: A Self Regularized Non-Monotonic Neural Activation Function，其函数及其导函数定义如下：

$$\begin{array}{rl}& \mathrm{M}\mathrm{i}\mathrm{s}\mathrm{h}=x\times \tanh (\ln (1+e^x))\\ & \ln (1+e^x)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{p}\mathrm{l}\mathrm{u}\mathrm{s}\end{array}$$
$$\begin{array}{rl}& {\mathrm{M}\mathrm{i}\mathrm{s}\mathrm{h}}^{\prime }=\frac{e^x\omega }{{\delta }^2}\\ & \omega =4(x+1)+4e^{2x}+e^{3x}+e^x(4x+6)\\ & \delta =2e^x+e^{2x}+2\end{array}$$

其图像为：

8.2 Mish激活函数的优点

1. 上无界，下有界，上无界避免了由于封顶导致的饱和，理论上对负值的轻微允许可以有更好的梯度流，而不是像ReLU中的硬零边界，下有界能带来正则效果，减少过拟合
2. 平滑的激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化，Mish主要是在光滑性上优于其他的激活函数
3. 非单调性

8.3 Mish激活函数的缺点

1. 看函数和其导函数就知道，计算量爆炸

8. ReLU变体 — Swish激活函数

8.1 函数及其导函数定义

$$\begin{array}{rl}\mathrm{S}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{h}& =x\times \sigma (\beta x)\\ & =\frac{x}{1+e^{-\beta x}}\end{array}$$
$${\mathrm{S}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{h}}^{\prime }=\sigma (\beta x)+x\beta [\sigma (\beta x)(1-\sigma (\beta x))]$$

$\beta$ 可以是常数也可以是可学习的参数。当 $\beta =0$ 时，Swish就变成了一个线性函数，当 $\beta$ 趋于 $\infty$ 时，Swish就变成了ReLU。

函数图像如下：

8.2 Swish激活函数的优点

1. 上无界，下有界
2. 平滑的，非单调的，大部分常见的激活函数都是单调的
3. 非单调
4. 处处连续且可导，更容易训练

8.3 Swish激活函数的缺点

1. 计算量大 —— 影响模型前向推理速度
2. 不稳定 —— 在不同的任务中可能产生不同的效果，不一定优于ReLU

8. ReLU变体 — SiLU激活函数

SiLU激活函数和Swish激活函数是一样的，不知道谁抄了抄谁 。

---

9. 如何选择合适的激活函数？

1. 除非在二分类问题中，否则请小心使用Sigmoid函数
2. 可以试试Tanh，不过大多数情况下它的效果会比不上 ReLU 和 Maxout
3. 如果你不知道应该使用哪个激活函数， 那么请优先选择ReLU —— 如无必要，勿增实体，优先选择最简单的
   ReLU相较于其他激活函数，有着最低的计算代价和最简单的代码实现
4. 如果你使用了ReLU， 需要注意一下Dead ReLU问题， 此时你需要仔细选择 Learning rate， 避免出现大的梯度从而导致过多的神经元 “Dead” 。
5. 如果发生了Dead ReLU问题， 可以尝试一下Leaky ReLU，ELU等ReLU变体， 说不定会有很好效果。
   有能力生成零均值分布的激活函数，相较于其他激活函数更优，注意：
   1. 这些变体通过会花费更多的计算资源，会影响网络推理速度；
   2. 当网络表现出过拟合时，随机ReLU可能会有帮助；
   3. 对PReLU来说，因为增加了需要学习的参数，当且仅当有很多训练数据时才可以试试PReLU的效果

10. 梯度爆炸

梯度误差是在神经网络训练期间计算的方向和梯度，神经网络以正确的方向和数值更新网络权重。在深度网络或递归神经网络中，梯度误差可能在更新过程中累积，造成非常大的梯度。这反过来会导致网络权重的大量更新，进而导致网络不稳定。在极端情况下，权重值可能变得太大，以至于溢出并导致NaN值现成梯度爆炸现象。

梯度爆炸是通过指数增长发生的，通过在网络层（其值大于1.0）中重复乘以梯度。

10.1 梯度爆炸现象

10.1.1 比较明显的现象

1. 模型无法“加入”训练数据，比如损失函数很差
2. 模型不稳定，每次更新的损失变化很大
3. 模型损失在训练过程中变为NaN

10.1.2 不太明显的现象

1. 模型权重在训练期间很快变化很大
2. 模型权重在训练过程中变为NaN
3. 训练期间每个节点和层的梯度误差始终高于1.0

10.2 如何解决梯度爆炸

1. 重现设计神经网络
2. 减少网络层数、减小batch szie、截断梯度
3. 使用LSTM
4. 使用梯度裁剪 (clipnorm=1.0 clipvalue=0.5)
5. 使用权重正则 —— L1 & L2

11. 常见相关面试题

Q1：什么是激活函数，为什么需要激活函数？

激活函数是在神经网络层间输入与输出之间的一种函数变换，目的是为了加入非线性因素，增强模型的表达能力。

---

Q2：了解那些激活函数以及应用？

回答主要分两类（饱和/非饱和），以及应用场景等。有时候可能特定到具体经典模型，比如:

• LSTM用到Tanh
• Transfromer中用到ReLU
• Bert中用到GeLU
• YOLO用到Leaky ReLU
• …

---

Q3：梯度消失与梯度爆炸现象与原因以及解决办法？

参看梯度消失与梯度爆炸部分。

---

Q4：ReLU激活函数为什么会出现死神经元，解决办法？

除上文提到输入为负值时，ReLU的梯度为0造成神经元死亡。还有Learning rate太高导致在训练过程中参数更新太大。

解决办法主要有：

1. 优化参数
2. 避免将learning rate设置太大，或者使用Adam等自动调节learning rate的方法
3. 更换激活函数

---

Q5：如何选择激活函数？

参看激活函数选择部分，亦可加入特定模型的使用分析。

参考

1. https://zhuanlan.zhihu.com/p/427541517
2. https://zhuanlan.zhihu.com/p/172254089
3. https://zhuanlan.zhihu.com/p/98863801
4. https://blog.csdn.net/Roaddd/article/details/114794071