PCA主成分分析实战案例

遇到的问题：

X = df.loc[:,0:4].values#提取第0-3列
y = df.loc[:,4].values #提取第4列

报错：

TypeError: cannot do slice indexing on Index with these indexers [0] of type int

修改代码为：

X = df.iloc[:,0:4].values#提取第0-3列
y = df.iloc[:,4].values #提取第4列

python代码实现PCA降维处理：

伪代码：

1.去除平均值

2.计算协方差矩阵

3.计算协方差矩阵的特征值和特征向量

4.将特征值从大到小排序

5.保留最上面的N个特征向量

6.将数据转换到上述N个特征向量构建的新空间中

1、导入数据

import numpy as np
import pandas as pd
df = pd.read_csv('iris.data')
df.head()

# 原始数据没有给定列名的时候需要我们自己加上
df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
df.head()

split data table into data X and class labels y将数据表拆分为数据X和类标签y

X = df.iloc[:,0:4].values#提取第0-3列
y = df.iloc[:,4].values #提取第4列

2、展示数据特征

from matplotlib import pyplot as plt
import math

#展示标签
label_dict = {1: 'Iris-Setosa',
              2: 'Iris-Versicolor',
              3: 'Iris-Virgnica'}

#展示特征
feature_dict = {0: 'sepal length [cm]',
                1: 'sepal width [cm]',
                2: 'petal length [cm]',
                3: 'petal width [cm]'}

# 指定绘图区域大小
plt.figure(figsize=(8, 6))
for cnt in range(4): # 这里用子图来呈现4个特征
    plt.subplot(2, 2, cnt+1)
    for lab in ('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'):
        plt.hist(X[y==lab, cnt],
                     label=lab,
                     bins=10,
                     alpha=0.3,)
    plt.xlabel(feature_dict[cnt])
    plt.legend(loc='upper right', fancybox=True, fontsize=8)

plt.tight_layout()
plt.show()

3、数据标准化

一般情况下，在进行训练前，数据经常需要进行标准化处理。

from sklearn.preprocessing import StandardScaler
#计算训练集的平均值和标准差，以便测试数据集使用相同的变换。
X_std = StandardScaler().fit_transform(X)
print (X_std)

4.计算协方差

方差：
最先提到的一个概念，也是旋转坐标轴的依据。之所以使用方差作为旋转条件是因为：最大方差给出了数据的最重要的信息。
$\mathrm{var}(X)=\frac{{\sum }_{i-1}^n\left(X_i-\bar{X}\right)\left(X_i-\bar{X}\right)}{n-1}$

协方差：
用来衡量两个变量的总体误差，方差是协方差的一种特殊情况，即当两个变量相同。可以通俗的理解为：两个变量在变化过程中是否同向变化？还是反方向变化？同向或反向程度如何？取值为负∞到正∞仿照方差的定义，度量各个维度偏离其均值的程度，定义为：
$$\mathrm{cov}(X,Y)=\frac{{\sum }_{i-1}^n\left(X_i-X\right)\left(Y_i-Y\right)}{n-1}$$

由协方差的定义可以推出两个性质：
$$1\cdot \mathrm{cov}(X,X)=\mathrm{var}(X)$$
$$2\cdot \mathrm{cov}(X,Y)=\mathrm{cov}(Y,X)$$

协方差矩阵:
协方差只能处理二维问题（即两个特征X，Y），维数多了自然需要计算多个协方差，比如n维的数 据集需要计算 $\frac{n!}{(n-2)!\ast 2}$ 个协方差，自然而然我们会想到使用矩阵来组织这些数据，协方差定义:
$C_{n\times n}=\left(c_{i,j},c_{i,j}=\mathrm{cov}\left({\mathrm{Dim}}_i,{\mathrm{Dim}}_j\right)\right)$
$C=\left(\begin{array}{lll}\mathrm{cov}(x,x)& \mathrm{cov}(x,y)& \mathrm{cov}(x,z)\\ \mathrm{cov}(y,x)& \mathrm{cov}(y,y)& \mathrm{cov}(y,z)\\ \mathrm{cov}(z,x)& \mathrm{cov}(z,y)& \mathrm{cov}(z,z)\end{array}\right)$

可见，协方差是一个对称的矩阵，且对角线是各维度上的方差。正是由于协方差矩阵为对称矩阵所以矩阵分解后特征值所对应的特征向量一定无线性关系，且相互之间一定正交，即内积为零。

#计算协方差
mean_vec = np.mean(X_std, axis=0)#均值
cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)
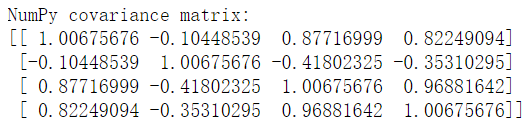
print('Covariance matrix \n%s' %cov_mat)

print('NumPy covariance matrix: \n%s' %np.cov(X_std.T))#numpy更简单

5.特征值和特征向量

对协方差矩阵的特征向量最直观的解释之一是它总是指向数据方差最大的方向（上面的u、v）。所以我们需要求得协方差矩阵，然后计算出其特征向量，通过对特征值的排序，选出我们要求的N个特征向量（即N个最重要特征的真实结构），用原数据乘上这N个特征向量而将它转换到新的空间中。（在numpy中linalg的eig方法可以求得特征值、特征向量，对特征值排序后选择最大的特征向量）

将二维特征降转为一维效果如下图（其它维数脑补）：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZlbLiKsj-1640161972021)

cov_mat = np.cov(X_std.T)#协方差矩阵

eig_vals, eig_vecs = np.linalg.eig(cov_mat)
#特征值和特征向量的提取

print('Eigenvectors \n%s' %eig_vecs)#特征向量
print('\nEigenvalues \n%s' %eig_vals)#特征值 表示特征向量的重要程度

# Make a list of (eigenvalue, eigenvector) tuples创建一个(特征值，特征向量)元组的列表
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
print (eig_pairs)
print ('----------')
# Sort the (eigenvalue, eigenvector) tuples from high to low将(特征值，特征向量)元组从高到低排序
eig_pairs.sort(key=lambda x: x[0], reverse=True)

# Visually confirm that the list is correctly sorted by decreasing eigenvalues
#视觉上确认列表是按特征值递减的顺序正确排序的
print('Eigenvalues in descending order:')
for i in eig_pairs:
    print(i[0])

#特征值归一化
tot = sum(eig_vals)
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]
print (var_exp)
cum_var_exp = np.cumsum(var_exp)#元素累计和
cum_var_exp

6.特征值的可视化

plt.figure(figsize=(6, 4))

plt.bar(range(4), var_exp, alpha=0.5, align='center',
            label='individual explained variance')
plt.step(range(4), cum_var_exp, where='mid',
             label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

7.降维

#取两个特征值最大的对应的两个特征向量构成映射基
matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1),
                      eig_pairs[1][1].reshape(4,1)))

print('Matrix W:\n', matrix_w)

#降维
Y = X_std.dot(matrix_w)#取两数的乘积
Y

8.效果对比

plt.figure(figsize=(6, 4))
#没有做降维处理，随机取两个特征
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
                        ('blue', 'red', 'green')):
     plt.scatter(X[y==lab, 0],
                X[y==lab, 1],
                label=lab,
                c=col)
plt.xlabel('sepal_len')
plt.ylabel('sepal_wid')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

plt.figure(figsize=(6, 4))
#PCA降维处理后的两个组成的特征
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
                        ('blue', 'red', 'green')):
     plt.scatter(Y[y==lab, 0],
                Y[y==lab, 1],
                label=lab,
                c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()