HMAC-SHA256
这里来学习一下前辈的关于HMAC-SHA256的文章
HMAC-SHA256是什么?
HMAC是密钥相关的哈希运算消息认证码(Hash-based Message Authentication Code)的缩写,由H.Krawezyk,M.Bellare,R.Canetti于1996年提出的一种**基于Hash函数和密钥进行消息认证的方法,**并于1997年作为RFC2104被公布,并在IPSec和其他网络协议(如SSL)中得以广泛应用,现在已经成为事实上的Internet安全标准。它可以与任何迭代散列函数捆绑使用。
人话:HMAC是一种使用单向散列函数来构造消息认证码的算法。
(单向散列函数,又称单向Hash函数、杂凑函数,就是把任意长度的输入消息串变化成固定长的输出串且由输出串难以得到输入串的一种函数。这个输出串称为该消息的散列值。一般用于产生消息摘要,密钥加密等。)
HMAC算法利用哈希运算,以一个密钥和一个消息为输入,生成一个消息摘要作为输出。
其安全性是建立在Hash加密算法基础上的。它要求通信双方共享密钥、约定算法、对报文进行Hash运算,形成固定长度的认证码。
通信双方通过认证码的校验来确定报文的合法性。HMAC算法可以用来作加密、数字签名、报文验证等[2]。
HMAC使用的Hahs函数并不仅限于一种,任何高强度的单向散列函数都可以被用于HMAC,如果将来设计出的新的单向散列函数,也同样可以使用。
使用SHA-1、SHA-224、SHA-256、SHA-384、SHA-512所构造的HMAC,分别称为HMAC-SHA1、HMAC-SHA-224、HMAC-SHA-256、HMAC-SHA-384、HMAC-SHA-512[1]。其中HMAC-SHA256就是接下来要重点介绍的。
HMAC-SHA256算法原理
定义1 HMAC算法
HMAC算法的数学公式为:
HMAC ( k , m ) = H ( k’ ⊕ opad , H ( k’ ⊕ ipad, m ) )
其中:
H 为密码Hash函数(如MD5或SHA-2),能够对明文进行分组循环压缩;
k 为密钥(secret key);
m 为要认证的消息;
k’ 是从原始密钥 k 导出的另一个密钥(如果 k 短于散列函数的输入块大小,则向右填充零;如果比该块大小更长,则对 k 进行散列)(这里用的估计就是PBKDF2)
ipad 内部填充(0x5C5C5C…5C5C,一段十六进制常量);
opad 外部填充(0x363636…3636,一段十六进制常量)。
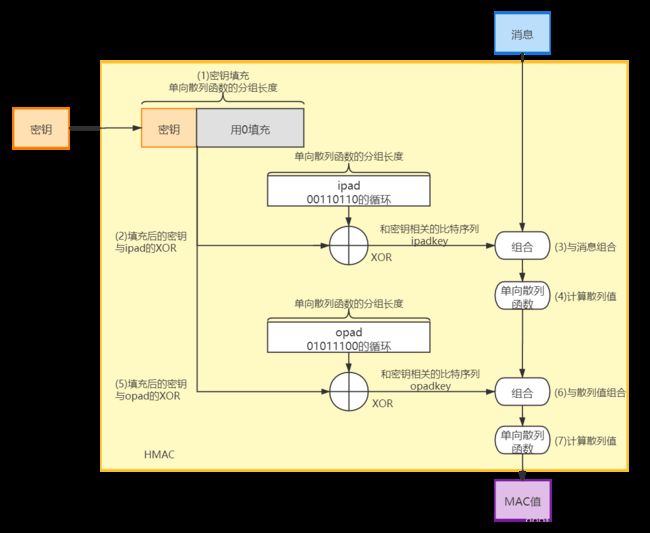
HMAC的计算步骤
如果密钥比单向散列函数分组长度要短,就需要在末尾填充0,直到其长度达到单向散列函数的分组长度为止。
如果密钥比分组长度要长,则要用单向散列函数求出密钥的散列值,然后将这个散列值用作HMAC的密钥。
② 处理后的密钥与ipad进行XOR
将处理后的密钥与被称为ipad的比特序列进行XOR运算。ipad是将00110110这一比特序列不断循环反复直到达到分组长度所形成的比特序列,其中ipad的i是inner的意思。
XOR运算所得到的值,是一个和单向散列函数的分组长度相同,且和密钥相关的比特序列。这里将这个比特序列称为ipadkey。
③ 与消息组合
随后,将ipadkey与消息组合,也就是将和密钥相关的比特序列(ipadkey)附加在消息的开头。
④ 计算散列值
将步骤③的结果作为单向散列函数的输入,并计算出散列值。
⑤ 处理后的密钥与opad进行XOR
将填充后的密钥与被称为opad的比特序列进行XOR运算,opad是将01011100这一比特序列不断循环反复直到达到分组长度所形成的比特序列,其中opad的o是outer的意思。
XOR运算所得到的结果也是一个和单向散列函数的分组长度相同,且和密钥相关的比特序列。这里将这个比特序列称为opadkey。
⑥ 与散列值组合
将步骤④的结果拼在opadkey的后面。
⑦ 计算散列值
将步骤⑥的结果输入单向散列函数,并计算出散列值,这个散列值就是最终的MAC值。
通过上述流程可以看出,最后得到的MAC值,一定是一个和输入的消息以及密钥都相关的长度固定的比特序列。
SHA-256算法
什么是SHA-256算法?
散列函数它被认为是一种单向函数——根据函数输出的结果,极难回推输入的数据。散列函数把消息数据打乱混合,压缩成散列值(摘要),使得数据量变小。
SHA-256由美国国家安全局研发,是SHA-2下细分出的一种算法,属于SHA算法之一,是SHA-1的后继者。SHA-256(Secure Hash Algorithm 256,安全散列算法256)是散列函数(或哈希函数)的一种,对于任意长度的消息,SHA256都会产生一个256-bit(32-byte数组)的哈希值,称作消息摘要。
摘要通常用一个长度为64位的十六进制字符串来表示。当接收到消息的时候,这个消息摘要可以用来验证数据是否发生改变,即验证其完整性。[2]
SHA-256的算法描述
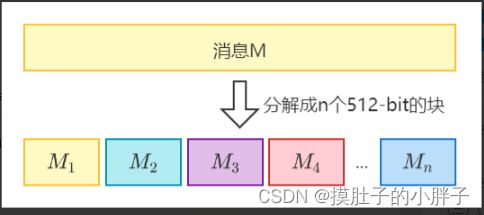
首先进行信息预处理,如下图所示,将原始消息分成若干个512-bit大小的消息块。最后一个消息块需要进行信息补全,并附上原消息的长度信息。消息被分成n块后,需要进行n次迭代,最后一次的结果就是最终的哈希值,即256bit的数字摘要。
在16位的系统中(比如8086微机) 1字 (word)= 2字节(byte)= 16(bit)
在32位的系统中(比如win32) 1字(word)= 4字节(byte)=32(bit)
在64位的系统中(比如win64)1字(word)= 8字节(byte)=64(bit)
SHA256算法的最小运算单元为“字”(word, 32-bit)。下图的256-bit的中间状态Hi被描述为8个字。
512-bit的消息块Mi将由16个字扩展为64个字,并与Hi混合,压缩成新的散列值Hi+1。
第i块数据经Map函数映射的结果,将作为第i+1块的输入,即Map(H_(i-1))=H_i。H0是预设好的hash初值(自然数中前8个质数的平方根的小数部分,取前32-bit),依次对数据进行Hash映射,得到的最后一个状态Hn便是最终的数字摘要。
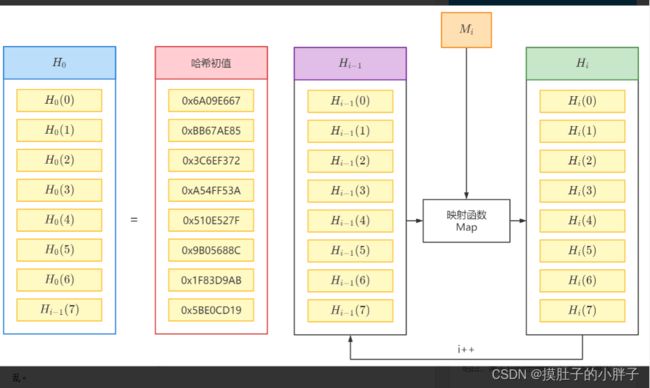
而其中最关键的操作为映射函数Map,其内部相当于是一个循环加密的过程,不断将原始信息进行打乱。
HMAC-SHA256算法实现
HMAC-SHA256算法,即使用SHA-256生成哈希值的HMAC算法。
依据HMAC算法和SHA-256算法内容,可知HMAC-SHA256算法的明文分组长度B为512-bit,可通过任意长度密钥K(最小推荐长度为256-bit,一般应大于B),得出长度为256-bit散列值(摘要)。定义为:
〖HMAC〗_SHA256 (k,m)= SHA256(k’⊕opad∥SHA256(k’⊕ipad∥m))
其中:
SHA256 为SHA-256加密算法,其输出散列值长度256-bit;
|| 拼接操作,将两个字符串拼接在一起;
B Hash函数明文分组长度,SHA-256算法中为512-bit;
k 为密钥(secret key);
m 为要认证的消息;
k’ 是从原始密钥 k 导出的另一个密钥(若 k 短于B,则向右填充零,直到与B相同;若k长于B,则对 k 进行一次SHA256散列计算)
ipad 内部填充(0x5C5C5C…5C5C,512-bit常量);
opad 外部填充(0x363636…3636,512-bit常量)。
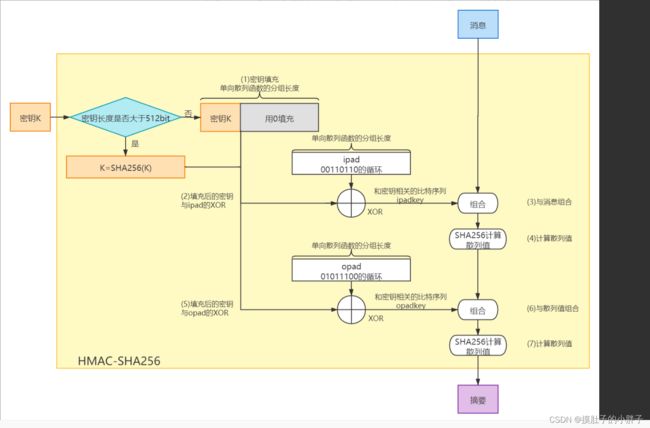
HMAC-SHA256的算法步骤
如果密钥比SHA-256分组长度(512-bit)要短,就需要在末尾填充0,直到其长度达到单向散列函数的分组长度为止。
如果密钥比SHA-256分组长度(512-bit)要长,则要用SHA-256算法求出密钥的散列值,然后将这个散列值用作HMAC的密钥。
② 处理后的密钥与ipad进行XOR
将处理后的密钥与被称为ipad的比特序列进行XOR运算。ipad是将00110110这一比特序列不断循环反复直到达到SHA-256分组长度(512-bit)所形成的比特序列,其中ipad的i是inner的意思。
XOR运算所得到的值,是一个和SHA-256分组长度(512-bit)相同,且和密钥相关的比特序列。这里将这个比特序列称为ipadkey。
③ 与消息组合
随后,将ipadkey与消息组合,也就是将和密钥相关的比特序列(ipadkey)附加在消息的开头。
④ 计算散列值
将步骤③的结果作为SHA-256函数的输入,并计算出散列值。
⑤ 处理后的密钥与opad进行XOR
将填充后的密钥与被称为opad的比特序列进行XOR运算,opad是将01011100这一比特序列不断循环反复直到达到SHA-256分组长度(512-bit)所形成的比特序列,其中opad的o是outer的意思。
XOR运算所得到的结果也是一个和SHA-256分组长度(512-bit)相同,且和密钥相关的比特序列。这里将这个比特序列称为opadkey。
⑥ 与散列值组合
将步骤④的结果拼在opadkey的后面。
⑦ 计算散列值
将步骤⑥的结果输入SHA-256函数,并计算出散列值,这个散列值就是最终的摘要内容。
通过上述流程可以看出,最后得到的摘要内容,一定是一个和输入的消息以及密钥都相关的长度固定的比特序列。
参考链接:
可搜索加密技术 - 学习笔记(二)- 预备知识:HMAC-SHA256函数
从零入门HMAC-SHA256
HMAC简介及HMAC-SHA256实现Demo