前缀、中缀、后缀表达式
我们平常使用的表达式一般为中缀表达式,而且一般只有中缀表达式有括号。
三种表达式
前缀表达式: +ab, 这种也叫做波兰式
中缀表达式: a+b, 这种正常表达式需要带括号, 而波兰式不用带括号
后缀表达式: ab+, 这种也叫做逆波兰式
一般而言,我们最常遇到中缀表达式转化为后缀表达式的方法。
中缀表达式转后缀表达式:
假定有中缀表达式1 + (( 2 + 3)* 4 ) – 5,请将它转化为后缀表达式。
方法一:利用表达式树
首先将中缀表达式转换为表达式树,然后后序遍历表达式树,所得结果就是后缀表达式。
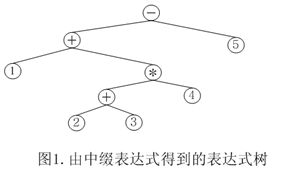
将中缀表达式转化为表达式树方法:表达式树的树叶是操作数,而其他的节点为操作符,根节点为优先级最低且靠右的操作符(如上述表达式优先级最低的是- 和+,但 + 更靠右,所以根为+),圆括号不包括。如上述中缀表达式转换后的表达式树如下:
经过后序遍历表达式树后得到的后缀表达式为:12 3 + 4 * + 5 –
方法二:利用辅助栈
从左到右遍历中缀表达式的每个操作数和操作符。
当读到操作数时,立即把它输出,即成为后缀表达式的一部分;
若读到操作符,判断该符号与栈顶符号的优先级,
若该符号优先级高于栈顶元素,则将该操作符入栈,
否则就一次把栈中运算符弹出并加到后缀表达式尾端,直到遇到优先级低于该操作符的栈元素,然后把该操作符压入栈中。
如果遇到”(”,直接压入栈中,如果遇到一个”)”,那么就将栈元素弹出并加到后缀表达式尾端,但左右括号并不输出。最后,如果读到中缀表达式的尾端,将栈元素依次完全弹出并加到后缀表达式尾端。
仍然以上面的表达式为例,其转换过程如下:
利用辅助栈后缀表达式与用表达式树的结果一样,都为:1 2 3 + 4 * + 5 –
#include
using namespace std;
const int maxSize = 20;
int getPriority(char i)
//得到符号的优先级
{
switch (i)
{
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
}
}
int infixToPostfix(char infix[],
char s2[])
{
char s1[maxSize];
//符号堆栈
int top1 = -1, top2 = -1;
//top1是符号堆栈的标号, top2是结果数组的标号
int stackMax = 0;
//记录堆栈最大处的标号
int i = 0;
//指向原数组的标号
while (infix[i] != '\0')
//控制循环的原数组循环的末尾
{
if (('a' <= infix[i] &&
infix[i] <= 'z') ||
(('0' <= infix[i] &&
infix[i] <= '9')))
//如果选到数字或者字母, 直接写入结果数组
{
s2[++top2] = infix[i];
i++;
}
else if (infix[i] == '(')
//如果遇到左括号, 直接写入符号堆栈
{
s1[++top1] = '(';
if (top1 > stackMax)
stackMax = top1;
i++;
}
else if (infix[i] == '+' ||
infix[i] == '-' ||
infix[i] == '*' ||
infix[i] == '/')
//如果遇到运算符则分类讨论
{
if (top1 == -1 ||
s1[top1] == '(' ||
getPriority(infix[i]) >
getPriority(s1[top1]))
//若在栈底, 在括号底, 或者操作符优先级高, 则操作符入栈
{
s1[++top1] = infix[i];
if (top1 > stackMax)
stackMax = top1;
i++;
}
else //否则出栈
s2[++top2] = s1[top1--];
}
else if (infix[i] == ')')
//如果遇到右括号, 则将其与对应左括号之间的符号出栈
{
while (s1[top1] != '(')
s2[++top2] = s1[top1--];
top1--;
i++;
}
}
while (top1 != -1)
//这里将堆栈中剩余的符号推出堆栈
s2[++top2] = s1[top1--];
return stackMax + 1;
//这里top1是堆栈标号, 必须+1才是数目
}
int main()
{
int top2 = -1;
char s2[maxSize];
char infix[maxSize] = "a+b-a*((c+d)/e-f)+g";
cout << infixToPostfix(infix, s2) << endl;
int i = 0;
while (s2[i] != '\0')
cout << s2[i++];
cout << endl;
return 0;
}
/*结果
5
ab+acd+e/f-*-g+
*/
方法三:加括号法/直接法
将中缀表达式(a+b)*c+d-(e+g)*h转换为后缀表达式
注意每一个配对的括号内都包含两个子表达式和一个运算符
((((a+b)*c)+d)-((e+g)*h))
随后将同一括号内的运算符提取到括号后
((((ab)+c)*d)+((eg)+h)*)-
随后将括号去除得到: ab+c*d+eg+h*-即为后缀表达式
后缀表达式转换为中缀表达式
假定有后缀表达式1 2 3 + 4 * +5 – ,请将它转化为前缀表达式。
方法一:利用表达式树
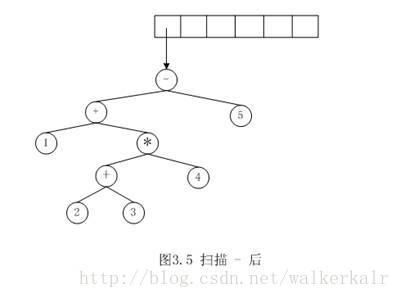
从左到右扫面后缀表达式,一次一个符号读入表达式。如果符号是操作数,那么就建立一个单节点树并将它推入栈中。如果符号是操作符,那么就从栈中弹出两个树T1和T2(T1先弹出)并形成一颗新的树,该树的根就是操作符,它的左、右儿子分别是T2和T1。然后将指向这棵新树的指针压入栈中。
前三个符号是操作数,因此创建三颗单节点树并将指向它们的指针压入栈中。
“+”被读入,因此指向最后两颗树的指针被弹出,形成一颗新树,并将指向新树的指针压入栈中。以下的流程图以相同原理执行。
最后再中序遍历所得的表达式树即得到我们所需的中缀表达式:1+((2+3)*4)-5
方法二:加括号法/直接法
将ab+c*d+eg+h*-转换为中缀表达式
从左到右逐个比较
遇到连续两个表达式加一个运算符的组合
即将其转换为中缀, 运算流程如下:
(a+b)c*d+eg+h*-
((a+b)*c)d+eg+h*-
(((a+b)*c)+d)eg+h*-
(((a+b)*c)+d)(e+g)h*-
(((a+b)*c)+d)((e+g)*h)-
((((a+b)*c)+d)-((e+g)*h))
(a+b)*c+d-(e+g)*h
————————————————
中缀表达式转换为前缀表达式
假定有中缀表达式1 + (( 2 + 3)* 4 ) – 5,请将它转化为前缀表达式。
方法一:利用表达式树
先将表达式用表达式树来表示,然后在前序遍历表达式树即得到我们所需的前缀表大式。表达式树前面已经介绍过,这里不再累赘。
此处,经过前序遍历所得前缀表达式为:- + 1 * + 2 3 4 5
方法二:利用辅助栈
首先构造一个运算符栈,然后从右至左扫描中缀表达式。如果是操作数,则直接输出,作为前缀表达式的一个直接转换表达式Temp(最后,前缀表达式由该表达式翻转得到);如果是运算符,则比较优先级:若该运算符优先级大于等于栈顶元素,则将该运算符入栈,否则栈内元素出栈并加到Temp表达式尾端,直到该运算符大于等于栈顶元素的优先级时,再将该运算符压入栈中。遇到右括号直接压入栈中,如果遇到一个左括号,那么就将栈元素弹出并加到Temp表达式尾端,但左右括号并不输出。最后,若运算符栈中还有元素,则将元素一次弹出并加到Temp表达式尾端,最后一步是将Temp表达式翻转。
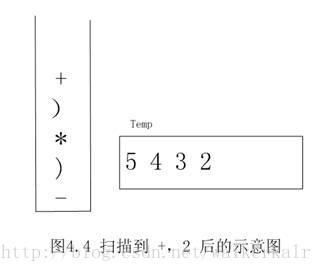
其过程如下图所示:
从右到左开始扫描,5为数字放入Temp中,-为操作符入栈。
遇到左括号,元素弹出直到遇到右括号为止。
所得前缀表达式为:- + 1 * + 2 3 4 5
#include
using namespace std;
const int maxSize = 20;
int getPriority(char i)
//得到符号的优先级
{
switch (i)
{
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
}
}
int getStringSize(char s[])
//注意仅用于字符数组
{
int i = 0;
while (s[i] != '\0')
i++;
return i;
}
int infixToPrefix(char infix[],
char s2[])
{
char s1[maxSize];
//符号堆栈
int top1 = -1, top2 = -1;
//top1是符号堆栈的标号, top2是结果数组的标号
int stackMax = 0;
//记录堆栈最大处的标号
int i = getStringSize(infix) - 1;
//指向原数组的标号, 注意转前缀是逆序
while (i != -1)
//控制循环的原数组循环的结束
{
if (('a' <= infix[i] &&
infix[i] <= 'z') ||
(('0' <= infix[i] &&
infix[i] <= '9')))
//如果选到数字或者字母, 直接写入结果数组
{
s2[++top2] = infix[i];
i--;
}
else if (infix[i] == ')')
//如果遇到右括号, 直接写入符号堆栈
{
s1[++top1] = ')';
if (top1 > stackMax)
stackMax = top1;
i--;
}
else if (infix[i] == '+' ||
infix[i] == '-' ||
infix[i] == '*' ||
infix[i] == '/')
//如果遇到运算符则分类讨论
{
if (top1 == -1 ||
s1[top1] == ')' ||
getPriority(infix[i]) >=
getPriority(s1[top1]))
//若在栈底, 在括号底, 或者操作符优先级高或者相等, 则操作符入栈
//注意转前缀时候入栈更简单, 优先级相同即可入栈
{
s1[++top1] = infix[i];
if (top1 > stackMax)
stackMax = top1;
i--;
}
else //否则出栈
s2[++top2] = s1[top1--];
}
else if (infix[i] == '(')
//如果遇到左括号, 则将其与对应右括号之间的符号出栈
{
while (s1[top1] != ')')
s2[++top2] = s1[top1--];
top1--;
i--;
}
}
while (top1 != -1)
//这里将堆栈中剩余的符号推出堆栈
s2[++top2] = s1[top1--];
return stackMax + 1;
//这里top1是堆栈标号, 必须+1才是数目
}
int main()
{
int top2 = -1;
char s2[maxSize];
char infix[maxSize] = "a+b-a*((c+d)/e-f)+g";
cout << infixToPrefix(infix, s2) << endl;
int i = getStringSize(s2) - 1;
while (i != -1)
cout << s2[i--];
cout << endl;
return 0;
}
/*结果
6
+-+ab*a-/+cdefg
*/
方法三:加括号法/直接法
将中缀表达式(a+b)*c+d-(e+g)*h转换为前缀表达式
注意每一个配对的括号内都包含两个子表达式和一个运算符
((((a+b)*c)+d)-((e+g)*h))
随后将同一括号内的运算符提取到括号前
-(+(*(+(ab)c)d)*(+(eg)h))
随后将括号去除得到: -+*+abcd*+egh即为前缀表达式
前缀表达式转换为中缀表达式:
假定有前缀表达式 - + 1 * + 23 4 5,请将它转化为中缀表达式。
方法一:辅助栈
首先创建一个数字栈。从右到左扫描前缀表达式,如果遇到操作数,则入栈。如果遇到操作符,则将栈顶元素弹出(后扫面的数字位于表达式前面),并和操作符结合写成表达式,作为中缀表达式。如果遇到的操作符优先级大于已存在表达式的最后执行操作符的优先级,则将已存在的表达式加上()。
如下是前缀表达式转为中缀表达式的示意图:
扫描到操作数直接入栈。
扫描到操作符,将两个栈顶元素弹出,并和操作符结合写成表达式。
表达式不是(2+3)*4,因为1比2、3、4后扫描到。
表达是不是5-(1+(2+3)*4),因为5是最早扫面到的数字。
所以中缀表达式为5-(1+(2+3)*4)。
————————————————
版权声明:本文为CSDN博主「walkerkalr」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/walkerkalr/article/details/22798365