Network in Network 算法解析

创新点

文章的新点：

1. 采用 mlpcon 的结构来代替 traditional 卷积层；

2. remove 卷积神经网络最后的 全连接层，采用 global average pooling 层代替；

mplconv 结构的提出：

conventional 的卷积层 可以认为是linear model , 为什么呢，因为 局部接收域上的每每一个tile 与 卷积核进行加权求和，然后接一个激活函数；它的 abstraction 的能力不够， 对处理线性可分的的 concept 也许是可以的，但是更复杂的 concepts 它有能力有点不够了，所以呢，需要引入 more potent 的非线性函数；

基于此，提出了 mlpcon 结构，它用多层的感知器（其实就是多层的全连接层）来替代单纯的卷积神经网络中的 加 权求和； mlpcon 指的是： multilayer perceptron + convolution;

两者的结构如下所示：其中下图的 Mlpconv 的有两层的隐含层；

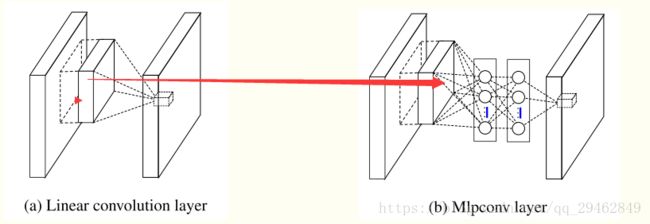
说明：在mlpconv中的每一层的后面都跟着一个 ReLU激活函数；用于加入更多的nonlinearity;

global average pooling 结构：

卷积神经网络最后的全连接层可以说作为了一个分类器，或者作为了一个 feature clustering. 它把卷积层学习到的特征进行最后的分类； intuitively, 根本不了解它是怎么工作的， 它就像一个黑盒子一样，并且它也引入了很多的参数，会出现 overfitting 现象； （我认为其实最后的 全接层就是一个分类器）

本文，remove掉了 全连接层， 使用 global average pooling 来代替； 举个例子更容易说明白： 假设分类的任务有100 classes， 所以设置网络的最后的 feature maps 的个数为 100， 把每一个feature map 看作成 对应每一类的 概率的相关值 ，然后对每一个 feature map 求平均值（即 global average pooling), 得到了 100维的向量， 把它直接给 softmax层，进行分类；（其实100个数中最大值对应的类别即为预测值， 之所以再送给 softmax层是为了求 loss，用于训练时求梯度）

网络的整体结构：

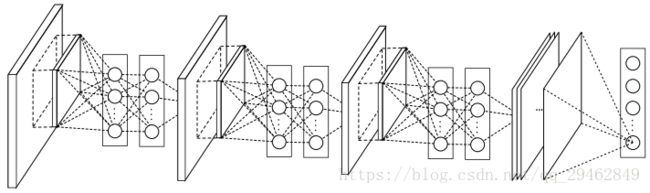
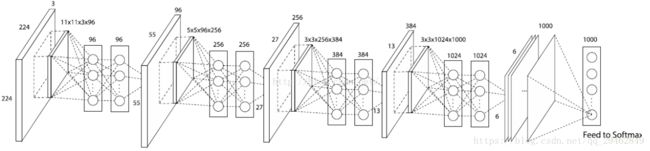
mlpconv 的细节：

输入为一个feature map, 输出为一个feature map 时：

输入为多个feature map, 输出为一个feature map 时：

输入为多个feature map, 输出为多个feature map 时：

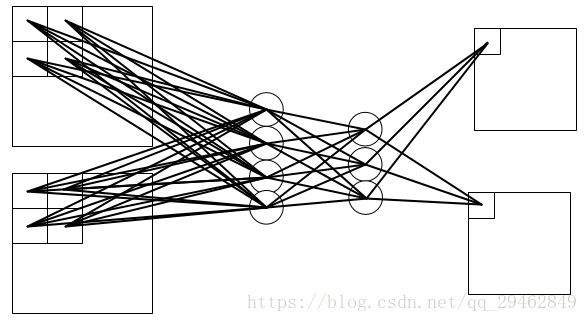
发现了什么 ？

在 卷积神经网络中，无论是输入还是输出，不同的 feature map 之间的卷积核是不相同的；

在mlpconv中，不同的 feature map 之间的开头与能结尾之间的权值不一样，而在 隐含层之间的权值是共享的；

另外：

全连接层之间可以看作一特殊的卷积层，其中卷积核的大小为 1*1， feature maps的 个数即为全连接层中的每一层的units的数目；

所以呢，假设上面的第三个图中的输入为2*（4*4）， 输出为2 *（3*3）时：

第一层的卷积核大小为2*2， 步长为1， 输入为2*（4*4）， 输出为4*（3*3）；

第二层的卷积核大小为1*1， 步长为1， 输入为4*（3 3）， 输出为 3（3*3）；

第三层的卷积核大小为1*1， 步长为1， 输入为3*（3*3)， 输出为 2*（3*3）；

global average pooling 的细节：

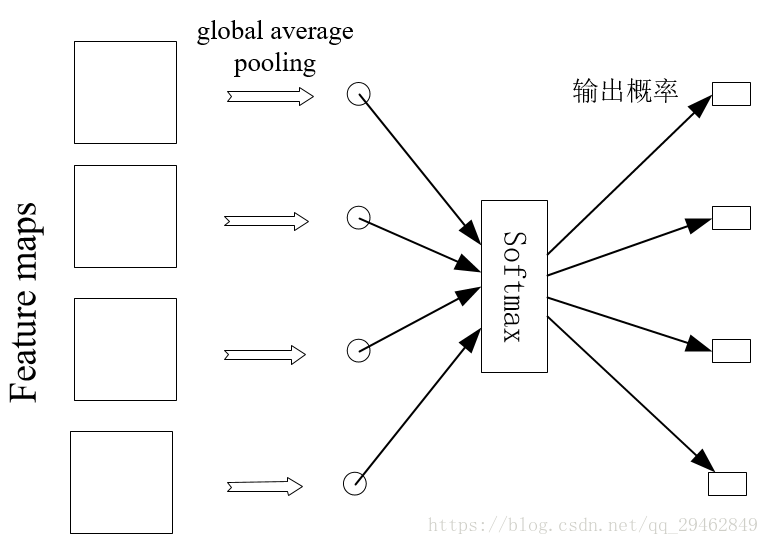
当分类的类别有4种时，则最后的 global average pooling 应该是这样的：

NIN结构的caffe实现：

因为我们可以把全连接层当作为特殊的卷积层，所以呢， NIN在caffe中是非常 容易实现的：NIN Caffe Code~这是由BVLC（Berkeley Vision Learning Center）维护的一个caffe的各种model及训练好的参数权值，可以直接下载下来用的；

其它：

文中的观点：通过实验说明了 global average pooling 也可以起到很好的 regular的作用。

另外，一个比较有趣地地方就是：在 可视化最后一层 feature maps时，它的激活区域与原始图片中目标所在的区域竟然相似；amazing!