北京大学Tensorflow2.0学习笔记 -- 神经网络优化篇
Tensorflow2.0 学习笔记 – 神经网络优化篇
本讲目标:学会神经网络优化过程,使用正则化减少过拟合,使用优化器更新网络参数
预备知识
条件选择函数 tf.where(条件语句,真返回A,假返回B)
a = tf.constant([1,2,3,1,1])
b = tf.constant([0,1,3,4,5])
# 若a>b,返回a对应位置的元素,否则返回b对应位置的元素
c = tf.where(tf.greater(a,b),a,b)
print(c)
运行结果:
![]()
返回一个[0,1)之间的随机数 np.random.RandomState.rand(维度)
import numpy as np
rdm = np.random.RandomState(seed=1)#seed=常数每次生成随机数相同
a = rdm.rand() # 返回一个随机标量
b = rdm.rand(2,3)# 返回维度为2行3列随机数矩阵
print("a:",a)
print("b:",b)
运行结果:

将两个数组按垂直方向叠加 np.vstack(数组1,数组2)
a = np.array([1,2,3])
b = np.array([4,5,6])
c = np.vstack((a,b))
print("c:\n",c)
运行结果:

网格函数 np.mgrid[起始值:结束值:步长,起始值:结束值:步长,…],x.ravel() 将x变为一维数组(即把当前变量拉直),np.c_[数组1,数组2,…] 使返回的间隔数值点配对
x,y = np.mgrid[1:3:1,2:4:0.5] # [起始值,结束值)
grid = np.c_[x.ravel(),y.ravel()]
print("x:",x)
print("y:",y)
print("grid:\n",grid)
运行结果:我们可以把它理解为两个数组元素进行(无序对)全排列组合

神经网络复杂度
- 空间复杂度:
层数 = 隐藏层的层数 + 1个输出层
总参数 = 总 w w w参数个数 + 总 b b b参数个数 - 时间复杂度:
乘加运算次数
指数衰减学习率
- 可以先用较大的学习率,快速得到较优解,然后逐步减小学习率,是模型在训练后期稳定
- 指数衰减学习率 = 初始学习率 × 学习衰减率(当前轮数/多少轮衰减一次)
import tensorflow as tf
w = tf.Variable(tf.constant(5, dtype=tf.float32))
epoch = 40
LR_BASE = 0.2
LR_DECAY = 0.99
LR_STEP = 1
for epoch in range(epoch): # for epoch 定义顶层循环,表示对数据集循环epoch次,此例数据集数据仅有1个w,初始化时候constant赋值为5,循环40次迭代。
with tf.GradientTape() as tape: # with结构到grads框起了梯度的计算过程。
lr = LR_BASE * LR_DECAY ** (epoch/LR_STEP)
loss = tf.square(w + 1)
grads = tape.gradient(loss, w) # .gradient函数告知谁对谁求导
w.assign_sub(lr * grads) # .assign_sub 对变量做自减 即:w -= lr*grads 即 w = w - lr*grads
print("After %s epoch,w is %f,loss is %f" % (epoch, w.numpy(), loss))
激活函数
优秀的激活函数
【非线性】:激活函数非线性时,多层神经网络可逼近所有函数
【可微性】:优化器大多用梯度下降更新参数
【单调性】:当激活函数是单调的,能保证单层网络的损失函数是凸函数
【近似恒等性】: f ( x ) ≈ x f(x) ≈x f(x)≈x当参数初始化为随机小值时,神经网络更稳定
激活函数输出值的范围:
- 激活函数输出为有限值时,基于梯度的优化方法更稳定
- 激活函数输出为无限值时,建议调小学习率
损失函数
-
S i g m o i d Sigmoid Sigmoid 函数 tf.nn.sigmoid(x)
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1+e^{-x}} f(x)=1+e−x1

特点:(1)易造成梯度消失;(2)输出非0均值,收敛速度慢;(3)幂运算复杂,训练时间长 -
T a n h Tanh Tanh 函数 tf.math.tanh(x)
f ( x ) = 1 − e − 2 x 1 + e − 2 x f(x) = \frac{1-e^{-2x}}{1+e^{-2x}} f(x)=1+e−2x1−e−2x

特点:(1)输出是0均值;(2)易造成梯度消失;(3)幂运算复杂,训练时间长 -
R e L u ReLu ReLu 函数 tf.nn.relu(x)
f ( x ) = m a x ( x , 0 ) f(x)=max(x,0) f(x)=max(x,0)

【优点】:解决了梯度消失问题;只需判断是否大于0,计算速度快;收敛速度远快于sigmoid和tanh
【缺点】:输出非0均值,收敛速度慢;Dead ReLu问题:某些神经元可能被激活,导致相应的参数永远不能被更新**(改进方法:避免过多的负数特征送入relu函数,即通过设置更小的学习率,减少参数分布的巨大变化)** -
L e a k y R e L U Leaky ReLU LeakyReLU 函数 tf.nn.leaky_relu(x)
f ( x ) = m a x ( a x , x ) f(x)=max(ax,x) f(x)=max(ax,x) 是对ReLU函数的一个微调,尽可能减少负数特征造成参数长期难以更新

激活函数对于初学者的建议:
- 首选ReLU激活函数
- 学习率设置最小值
- 输入特征标准化,即让输入特征满足以0为均值,1为标准差的正态分布
- 初始参数中心化,即让随机生成的参数满足以0为均值, 2 当 前 输 入 特 征 层 数 \sqrt{\frac{2}{当前输入特征层数}} 当前输入特征层数2为标准差的分布
损失函数
- 损失函数(loss):预测值(y)与已知答案(y_)的差距
均方误差MSE
- 原始公式: M S E ( y _ , y ) = ∑ i = 1 n ( y − y _ ) 2 n MSE(y\_,y)=\frac{\sum_{i=1}^n(y-y\_)^2}{n} MSE(y_,y)=n∑i=1n(y−y_)2
- tensorflow API:
loss_mse = tf.reduce_mean(tf.square(y_-y))
交叉熵函数CE
- 用来表示两个概率分布之间的距离
- 原始公式: H ( y _ , y ) = − ∑ y _ ⋅ l n y H(y\_,y)=-\sum{y\_\cdot lny} H(y_,y)=−∑y_⋅lny
- tensorflow API:
loss_ce = tf.losses.categorical_crossentropy(y_,y)
loss_ce1 = tf.losses.categorical_crossentropy([1,0],[0.6,0.4])
loss_ce2 = tf.losses.categorical_crossentropy([1,0],[0.8,0.2])
print("loss_ce1:",loss_ce1)
print("loss_ce2:",loss_ce2)
# softmax与交叉熵结合:输出先过softmax函数,再计算y与y_的交叉熵损失函数
# tf.nn.softmax_cross_entropy_with_logits(y_,y)
y_ = np.array([[1,0,0],[0,1,0],[0,0,1],[1,0,0],[0,1,0]])
y = np.array([[12,3,2],[3,10,1],[1,2,5],[4,6.5,1.2],[3,6,1]])
y_pro = tf.nn.softmax(y)
loss_ce1 = tf.losses.categorical_crossentropy(y_,y_pro)
loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_,y)
print("分步计算的结果:\n",loss_ce1)
print("结合计算的结果: \n",loss_ce2)
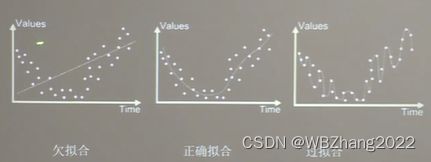
欠拟合与过拟合
- 欠拟合的解决办法:增加输入特征项;增加网络参数;减少正则化参数
- 过拟合的解决办法:数据清洗;增大训练集;采用正则化;增大正则化参数
正则化减少过拟合
正则化在损失函数中引入模型复杂度指标,利用给 w w w 加权值,弱化了训练数据的噪声(一般不正则化 b b b)

正则化的选择:
- L1正则化:大概率会使很多参数变为0,因此该方法可通过稀疏参数,即减少参数的数量,降低复杂度
- L2正则化:会使参数很接近零但不为零,因此该方法可通过减小参数值的大小降低复杂度
优化器更新网络参数
待优化参数 w w w ,损失函数 l o s s loss loss,学习率 l r lr lr,每次迭代一个batch,t表示当前batch迭代的总次数:
- 计算 t t t 时刻损失函数关于当前参数的梯度 g t = ∇ l o s s = ∂ l o s s ∂ w t g_t=\nabla loss=\frac{\partial{loss}}{\partial{w_t}} gt=∇loss=∂wt∂loss
- 计算 t t t 时刻一阶动量 m t m_t mt 和动量 V t V_t Vt
- 计算 t t t 时刻下降梯度: η t = l r ⋅ m t / V t \eta_t=lr \cdot m_t/\sqrt{V_t} ηt=lr⋅mt/Vt
- 计算 t + 1 t+1 t+1 时刻参数: w t + 1 = w t − η t = w t − l r ⋅ m t / V t w_{t+1}=w_t-\eta_t=w_t-lr \cdot m_t/\sqrt{V_t} wt+1=wt−ηt=wt−lr⋅mt/Vt
一阶动量:与梯度相关的函数
二阶动量:与梯度平方相关的函数
随机梯度下降SGD
m t = g t V t = 1 m_t=g_t\quad V_t=1 mt=gtVt=1
η = l r ⋅ m t / V t = l r ⋅ g t \eta=lr\cdot m_t/\sqrt{V_t}=lr\cdot g_t η=lr⋅mt/Vt=lr⋅gt
w t + 1 = w t − η ⋅ m t / V t = w t − l r ⋅ g t w_{t+1}=w_{t}-\eta \cdot m_t/\sqrt{V_t}=w_t-lr\cdot g_t wt+1=wt−η⋅mt/Vt=wt−lr⋅gt
即 w t + 1 = w t − l r ⋅ ∂ l o s s ∂ w t 即w_{t+1}=w_t-lr\cdot\frac{\partial{loss}}{\partial{w_t}} 即wt+1=wt−lr⋅∂wt∂loss
#SGD
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b1自更新
含动量的随机梯度下降SGDM
m t = β ⋅ m t − 1 + ( 1 − β ) ⋅ g t V t = 1 m_t=\beta\cdot m_{t-1}+(1-\beta)\cdot g_t\quad V_t=1 mt=β⋅mt−1+(1−β)⋅gtVt=1
η t = l r ⋅ m t / V t = l r ⋅ m t = l r ⋅ β ⋅ m t − 1 + ( 1 − β ) ⋅ g t \eta_t=lr \cdot m_t/\sqrt{V_t}=lr\cdot m_t=lr\cdot\beta\cdot m_{t-1}+(1-\beta)\cdot g_t ηt=lr⋅mt/Vt=lr⋅mt=lr⋅β⋅mt−1+(1−β)⋅gt
w t + 1 = w t − η t = w t − l r ⋅ ( β ⋅ m t − 1 + ( 1 − β ) ⋅ g t ) w_{t+1}=w_t-\eta_t=w_t-lr\cdot(\beta\cdot m_{t-1}+(1-\beta)\cdot g_t) wt+1=wt−ηt=wt−lr⋅(β⋅mt−1+(1−β)⋅gt)
m_w,m_w = 0,0
beta = 0.9
# sgd-momentun
m_w = beta * m_w + (1-beta) * grads[0]
m_b = beta * m_b + (1-beta) * grads[1]
w1.assigned_sub(lr*m_w)
b1.assigned_sub(lr*m_b)
Adagrad
在SGD基础上增加二阶动量
m t = g t V t = ∑ τ = 1 t g τ 2 m_t=g_t\quad V_t=\sum_{\tau=1}^{t}g_{\tau}^2 mt=gtVt=∑τ=1tgτ2
η t = l r ⋅ m t / ( V t ) = l r ⋅ g t / ∑ τ = 1 t g τ 2 \eta_t=lr\cdot m_t/(\sqrt{V_t})=lr\cdot g_t/ \sqrt{\sum_{\tau=1}^{t}g_{\tau}^2} ηt=lr⋅mt/(Vt)=lr⋅gt/∑τ=1tgτ2
w t + 1 = w t − η t = w t − l r ⋅ g t / ∑ τ = 1 t g τ 2 w_{t+1}=w_t-\eta_t=w_t-lr\cdot g_t/\sqrt{\sum_{\tau=1}^{t}g_{\tau}^2} wt+1=wt−ηt=wt−lr⋅gt/∑τ=1tgτ2
v_w,v_b = 0,0
#adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w)
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b)
RMSProp
在SGD基础上增加二阶动量
m t = g t V t = β ⋅ V t − 1 + ( 1 − β ) ⋅ g t 2 m_t=g_t\quad V_t=\beta\cdot V_{t-1}+(1-\beta)\cdot g_{t}^2 mt=gtVt=β⋅Vt−1+(1−β)⋅gt2
η t = l r ⋅ m t / V t = l r ⋅ g t / ( β ⋅ V t − 1 + ( 1 − β ) ⋅ g t 2 ) \eta_t=lr\cdot m_t/\sqrt{V_t}=lr\cdot g_t/(\sqrt{\beta \cdot V_{t-1}+(1-\beta)\cdot g_t^2}) ηt=lr⋅mt/Vt=lr⋅gt/(β⋅Vt−1+(1−β)⋅gt2)
w t + 1 = w t − η t = w t − l r ⋅ g t / ( β ⋅ V t − 1 + ( 1 − β ) ⋅ g t 2 ) w_{t+1}=w_t-\eta_t=w_t-lr\cdot g_t/(\sqrt{\beta\cdot V_{t-1}+(1-\beta)\cdot g_{t}^2}) wt+1=wt−ηt=wt−lr⋅gt/(β⋅Vt−1+(1−β)⋅gt2)
v_w,v_b = 0,0
beta = 0.9
# adadelta
v_w = beta * v_w + (1-beta) * tf.square(grads[0])
v_b = beta * v_b + (1-beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
Adam
同时结合SGDM一阶动量和RMSProp二阶动量
m t = β 1 ⋅ m t − 1 + ( 1 − β 1 ) ⋅ g t m_t=\beta_1\cdot m_{t-1}+(1-\beta_1)\cdot g_t mt=β1⋅mt−1+(1−β1)⋅gt
修正一阶动量的偏差: m t ^ = m t 1 − β 1 t \hat{m_t}=\frac{m_t}{1-\beta_{1}^t} mt^=1−β1tmt
修正二阶动量的偏差: V t ^ = V t 1 − β 2 t \hat{V_t}=\frac{V_t}{1-\beta_{2}^t} Vt^=1−β2tVt
η t = l r ⋅ m t ^ / V t ^ = l r ⋅ m t 1 − β 1 t / V t 1 − β 2 t \eta_t=lr\cdot \hat{m_t}/\sqrt{\hat{V_t}}=lr\cdot\frac{m_t}{1-\beta_{1}^t}/\sqrt{\frac{V_t}{1-\beta_{2}^t}} ηt=lr⋅mt^/Vt^=lr⋅1−β1tmt/1−β2tVt
w t + 1 = w t − η t = w t − l r ⋅ m t 1 − β 1 t / V t 1 − β 2 t w_{t+1}=w_t-\eta_t=w_t-lr\cdot\frac{m_t}{1-\beta_{1}^t}/\sqrt{\frac{V_t}{1-\beta_{2}^t}} wt+1=wt−ηt=wt−lr⋅1−β1tmt/1−β2tVt
m_w,m_b = 0,0
v_w,v_b = 0,0
beta1,beta2 = 0.9,0.999
delta_w,delta_b = 0,0
global_step = 0
# Adam
m_w = beta1 * m_w + (1-beta1) * grads[0]
m_b = beta1 * m_b + (1-beta1) * grads[1]
v_w = beta2 * v_w + (1-beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1-beta2) * tf.square(grads[1])
m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))
w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))