蓝桥杯 试题 算法训练 数字游戏 C++ 详解

题目：

给定一个1～N的排列a[i]，每次将相邻两个数相加，得到新序列，再对新序列重复这样的操作，显然每次得到的序列都比上一次的序列长度少1，最终只剩一个数字。
例如:
  3  1  2  4
  4  3  6
  7  9
16
现在如果知道N和最后得到的数字sum，请求出最初序列a[i]，为1～N的一个排列。若有多种答案，则输出字典序最小的那一个。数据保证有解。

---

前言：

目前有 2 种方法求解：1.穷举 + 傻瓜式求解         2.穷举 + 找规律求解

但不管怎么样，穷举的方法都有必要掌握。

（下面分为： 一、自己纯手写实现穷举          二、利用C++库函数实现穷举）

---

开始：

零、穷举

本题考查的是关于 1 ~ N 的排列，字典序排列的穷举。

举例：

N = 2，字典序排列为：12，21 共2种（2 * 1）

N = 3，字典序排列为：123，132，213，231，312，321 共6种（3 * 2 * 1）

N = 4，字典序排列为：…… 共24种（4 * 3 * 2 * 1）

那么我们要做到，知道 N 就可以穷举出它的所有排序，按字典序来。

---

一、自己纯手写实现穷举

（写的时候没有上网查，我自己想了很久，所以我的方法也仅仅是一种参考，并不是最优解）

通过对 N = 3，N = 4，N = 5 进行纸上的推导，发现：

当 N = 3        初始状态：123

123 >> 132（将 2 和 3 互换）

132 >> 213（暂时没有规律）

213 >> 231（将 1 和 3 互换）

231 >> 312（没有发现什么规律，仅仅是肉眼知道2后面没有别的情况了，所以就把 2 改为 3 ）

312 >> 321（结束，目前知道，当倒数第一位比倒数第二位大的时候，那就交换它们）

这点很好理解嘛，从数学的角度，将个位大的数字与十位小的数字交换，就是这个数全排列的下一个数，比起和百位换，仅仅大一点点而已。这点相信大家小学或者初中的数学里面有接触到，给你若干个不同的数字，如果让你手写从小到大的全部排列，应该都会写吧。（现在我们就是把自己手写懂的方法用代码实现，关键就是找出其中的规律）

当 N = 4        初始状态：1234

1234 >> 1243（嗯，当倒数第一位比倒数第二位大的时候，交换它们）

1243 >> 1324（又是这种情况，找不出什么规律）

1324 >> 1342（同理）

1342 >> 1423

打住，这个时候我们可要找规律了，目前有 4 个情况，分别是：132，231，1243，1342

不知道你能不能看出什么规律，

这里我的发现是：当出现 (小的数) (大的数) (小的数) 的时候，意味着左边那个小的数的右边已经（饱和了）不能再变大了，这个时候需要更新左边那个小的数，即让它和它右边的一干数字中比它大的当中最小的数进行交换，还是举例：

132 的下一个全排 213，我们不管其他，就看是不是 1 是和它右边比它大的数 2,3 当中最小的数 2 进行交换的？是吧。再看：

231 的下一个全排 312，2 还是和它右边比它大的数 3 当中最小的数 3 进行交换的。同理：

1243 的下一个全排 1324，2 还是和它右边比它大的数 3,4 当中最小的数 3 进行交换的。

1342 的下一个全排 1423，3 还是和它右边比它大的数 4 当中最小的数 4 进行交换的。

同时，交换完以后左边那个小的数的右边是不是又要重新开始进行排列啊，我用的是冒泡排序。

---

推导结束。综合就是：如果倒数第一个数比倒数第二个数大，就交换它们（结束）。不然从右往左检查，如果有(小数)(大数)(小数)的情况，将左边的小数交换它右边比它大的数当中最小的那个数，然后对它右边进行从小到大的排序（结束）。

这就是我自己想出来的方法。代码如下：

#include
using namespace std;

bool func(int* p, int n)
{
	//标记是否退出
	int index_return = 1;

	//如果满足数组的每一项都比后一项大：例 12345 -> 54321
	for (int i = 1; i <= n - 2; i++)
	{
		if (*(p + i) < *(p + i + 1))
		{
			index_return = 0;
		}
	}
	
	//如果上面 if 语句一次 = 0 都没有执行，证明确实每一项都比后一项大，则证明穷举完毕。
	if (index_return == 1)
	{
		return false;
	}

	//如果倒数第一项比倒数第二项大，交换之，然后结束。
	if (*(p + n) > *(p + n - 1))
	{
		int temp = *(p + n);
		*(p + n) = *(p + n - 1);
		*(p + n - 1) = temp;
		return true;
	}

	//标记左一个小数的位置，下标。
	int index = 0;

	//循环数组，从右至左，查找(小数)(大数)(小数)
	for (int i = n - 1; i >= 1; i--)
	{
		if (*(p + i + 1) < *(p + i) && *(p + i) > *(p + i - 1))
		{
			//标记位置
			index = i - 1;

			//将左(小数)右一个视为第一个符合条件的数。
			int max_min = index + 1;

			//遍历左(小数)右边的数据，找出：比左(小数)大的数(当中)最小的数
			for (int j = index + 1; j <= n; j++)
			{
				//有则记录其位置，下标。
				if (*(p + j) > *(p + index) && *(p + j) < *(p + max_min))
				{
					max_min = j;
				}
			}

			//交换之
			int temp = *(p + max_min);
			*(p + max_min) = *(p + index);
			*(p + index) = temp;

			//记得退出
			break;
		}
	}

	//每次进行这样的交换后，其右边的数据都要进行排序(升序)
	for (int i = index + 1; i <= n - 1; i++)
	{
		for (int j = index + 1; j <= n - 1 - (i - index - 1); j++)
		{
			if (*(p + j) > *(p + j + 1))
			{
				int temp = *(p + j);
				*(p + j) = *(p + j + 1);
				*(p + j + 1) = temp;
			}
		}
	}
	return true;
}

int main()
{
	int n, sum;
	cin >> n >> sum;

	//定义 [11] 为了加多一个 0 填充，这样第几个数对应的下标也是几，方便上面函数的书写。
	int ii[11] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };

	//二维数组用于推导上面一维数组的结果。
	int ii_2[11][11] = { 0 };

	do
	{
		//将一维数组的结果拷贝到二维数组的第二行，下标是 1 ，方便写循环条件。
		for (int i = 1; i <= n; i++)
		{
			ii_2[1][i] = ii[i];
		}

		//进行推导
		for (int i = 2; i <= n; i++)
		{
			for (int j = 1; j < n - (i - 2); j++)
			{
				ii_2[i][j] = ii_2[i - 1][j] + ii_2[i - 1][j + 1];
			}
		}

		//如果符合条件则退出，不然一直循环到穷举完毕。
		if (ii_2[n][1] == sum)
		{
			for (int i = 1; i <= n; i++)
			{
				cout << ii_2[1][i] << " ";
			}
			break;
		}
	//穷举完毕，函数将返回false，自然也会退出循环。
	} while (func(ii, n));

	return 0;
}

---

二、利用C++库函数实现穷举

介绍：next_permutation(数组元素起始位置，数组元素结束位置);//作用是求下一个字典序排列

【还有prev_permutation()函数，作用是求上一个字典序排列。有空可以了解一下】

还是C++库函数更加强大，还可以对字符进行排序。

这样代码更加简洁，可以写成：

#include
using namespace std;
#include

int main()
{
	int n, sum;
	cin >> n >> sum;

	int ii[11] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };

	int ii_2[11][11] = { 0 };

	do
	{
		for (int i = 1; i <= n; i++)
		{
			ii_2[1][i] = ii[i];
		}

		for (int i = 2; i <= n; i++)
		{
			for (int j = 1; j < n - (i - 2); j++)
			{
				ii_2[i][j] = ii_2[i - 1][j] + ii_2[i - 1][j + 1];
			}
		}

		if (ii_2[n][1] == sum)
		{
			for (int i = 1; i <= n; i++)
			{
				cout << ii_2[1][i] << " ";
			}
			break;
		}

	} while (next_permutation(ii + 1, ii + n + 1));

	return 0;
}

这是在我之前的代码基础上面修改的，当然是可以再优化的。

---

比如上面都是：穷举 + 傻瓜式求解

可以在判断条件上面优化：穷举 + 找规律求解

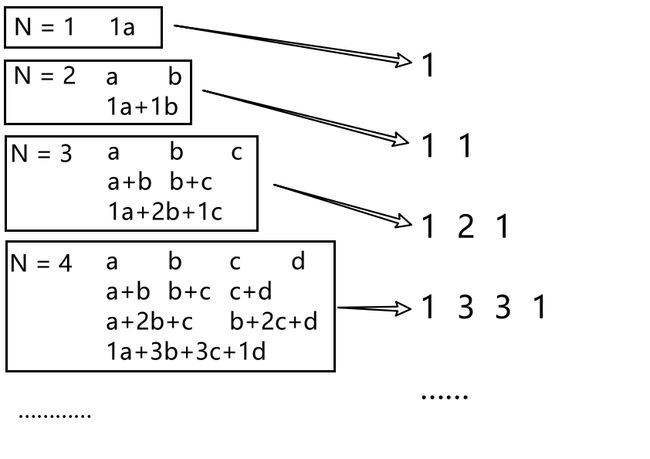
找规律：

知道这个规律，只需要将得到的字典序排列分别 乘与 对应的杨辉三角再求和判断即可。

这样就不用将字典序排列放在二维数组中进行推导查看结果了，更加高效。

---

分享我的想法就到这里，接下来就靠各位同学自行去思考和优化了。

（赶着做下一题去了……）