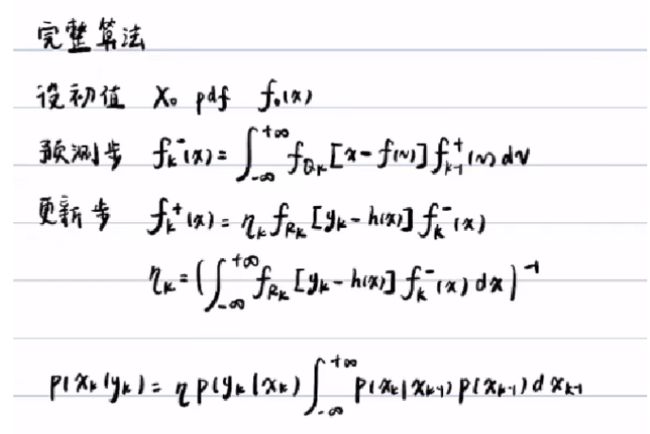opencv学习记录2-Kalman滤波

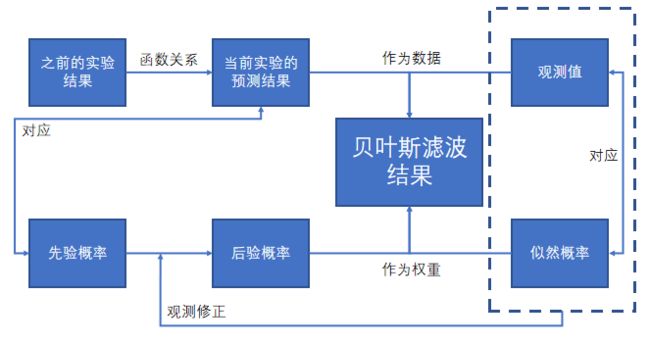
贝叶斯滤波

1.理论

贝叶斯推断方法的关键是任何推断都必须且只须根据后验分布，而不能再涉及样本分布

2.贝叶斯滤波的基本方法：

优缺点：

• 优点：可以有效滤除噪声，得到比较精准的状态估计

• 缺点：需要做无穷积分，大多数情况下没有解析解

卡尔曼滤波是它的改进版）

实例

利用opencv自带的kalmanfilter类实现对鼠标轨迹的跟踪

步骤

卡尔曼滤波器算法分为两个阶段：

1. 预测：使用由当前点计算的协方差来估计目标的新位置

2. 更新：记录目标的位置，并为下一次循环计算修正协方差

kalman = cv2.KalmanFilter(4, 2)

表示Kalman滤波器转移矩阵维度为4，测量矩阵维度为2

（因为状态量有4个：x，y方向分别的位移和速度，可观测的量有2个：x，y方向的位移）

测量矩阵：

转移矩阵：

例：

kalman.measuremenMatrix = np.array([[1, 0, 0, 0], [0, 1, 0, 0]], np.float32)
kalman.transitionMatrix = np.array([[1, 0, 1, 0], [0, 1, 0, 1],
                                    [0, 0, 1, 0], [0, 0, 0, 1]], np.float32)

过程噪声和测量噪声以一个经验值估计（来源csdn）

kalman.processNoiseCov = np.array([[1, 0, 0, 0], [0, 1, 0, 0],
                                   [0, 0, 1, 0], [0, 0, 0, 1]], np.float32) * 0.003
kalman.measurementNoiseCov = np.array([[1, 0], [0, 1]], np.float32) * 0.5

具体操作：

3. 初始化数组，存放测量坐标和鼠标运动预测的数据

4. 传递进当前测量的坐标值

5. 修正卡尔曼滤波预测结果

6. 调用kalman类的predict，得到预测值矩阵（用来估算目标位置

7. 将上一次测量值和当前测量值连线；将上一次预测值和当前预测值连线

注意：

• Kalman这个类需要初始化下面变量：

转移矩阵，测量矩阵，控制向量(没有的话，就是0)，过程噪声协方差矩阵，测量噪声协方差矩阵，后验错误协方差矩阵，前一状态校正后的值，当前观察值。

• cv2.KalmanFilter(4,2)表示转移矩阵维度为4，测量矩阵维度为2

• 卡尔曼滤波模型假设k时刻的真实状态是从(k − 1)时刻的状态演化而来，符合下式：

        X(k) = F(k) * X(k-1) + B(k)*U(k) + W（k）

其中

F(k) 是作用在xk−1上的状态变换模型（/矩阵/矢量）。

B(k) 是作用在控制器向量uk上的输入－控制模型。

W(k) 是过程噪声，并假定其符合均值为零，协方差矩阵为Qk的多元正态分布。

完整代码：

import cv2
import numpy as np

# 创建一个画图区域
frame = np.zeros((700, 700, 3), np.uint8) 

# 初始化测量坐标和鼠标运动预测的数组
last_measurement = current_measurement = np.array((2, 1), np.float32)
last_prediction = current_prediction = np.zeros((2, 1), np.float32)

# 用来绘制跟踪结果
def mousemove(event, x, y, s, p):
    global frame, current_measurement, measurements, last_measurement, mcurrent_prediction, last_prediction
    # 把当前预测存储为上一次预测
    last_prediction = current_prediction 
    # 把当前测量存储为上一次测量
    last_measurement = current_measurement

   
    current_measurement = np.array([[np.float32(x)], [np.float32(y)]]) 
    # 用当前测量来校正卡尔曼滤波器
    kalman.correct(current_measurement) 
    # 计算卡尔曼预测值，作为当前预测
    current_prediction = kalman.predict() 

    # 上一次测量坐标
    lmx, lmy = last_measurement[0], last_measurement[1] 
    # 当前测量坐标
    cmx, cmy = current_measurement[0], current_measurement[1] 
    # 上一次预测坐标
    lpx, lpy = last_prediction[0], last_prediction[1] 
    # 当前预测坐标
    cpx, cpy = current_prediction[0], current_prediction[1] 

    # 绘制从上一次测量到当前测量以及从上一次预测到当前预测的两条线
    # 蓝色为测量值
    cv2.line(frame, (int(lmx), int(lmy)), (int(cmx), int(cmy)), (255, 0, 0)) 
    # 粉色为预测值
    cv2.line(frame, (int(lpx), int(lpy)), (int(cpx), int(cpy)), (255, 0, 255)) 

cv2.namedWindow("kalman_tracker")
cv2.setMouseCallback("kalman_tracker", mousemove)

# 4：状态数，包括（x，y，dx，dy）坐标及速度（每次移动的距离）；2：观测量，能看到的是坐标值
kalman = cv2.KalmanFilter(4, 2)
# 系统测量矩阵
kalman.measurementMatrix = np.array([[1, 0, 0, 0], [0, 1, 0, 0]], np.float32)
# 状态转移矩阵
kalman.transitionMatrix = np.array([[1, 0, 1, 0], [0, 1, 0, 1], [0, 0, 1, 0], [0, 0, 0, 1]], np.float32) 
# 系统过程噪声协方差
kalman.processNoiseCov = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]], np.float32)*0.03

while True:
    cv2.imshow("kalman_tracker", frame)
    key = cv2.waitKey(1) & 0xFF
    if key == ord('q'):
        break
cv2.destroyAllWindows()