GAMES202 笔记 -Real-Time Ray-Tracing
目录
一、Real Time Ray Tracing(RTRT)
RTX
光路样本
二、Industrial Sulution-temporal
motion vector
G-Buffers-几何缓冲区
Back projection
Temporal Accum./Denoising
三、Implementation of filtering
Gaussian filtering
Bilateral filtering-双边滤波
Joint Bilateral filtering-联合双边滤波
四、Implementing Large filters
Separate Passes(拆分实现)
Progressively Growing Sizes
五、Outlier Removal
Outlier Detection and Clamping
Temporal Clamping
六、Specific Filtering Approaches for RTRT
SVGF-Basic Idea
SVGF-Joint Bilateral Filtering
七、RAE(Recurrent AutoEncoder)
AutoEncoder
Comparison
一、Real Time Ray Tracing(RTRT)
RTX
RTX其本质上只是硬件的提升,并不涉及任何算法部分,在显卡加装了一个用来做光追的部件,由于光线追踪做的是光线与场景的求交,结合games101我们知道光线要经历BVH或者KD-tree这种加速结构,也就是做一个树的遍历从而快速判断光线是否与三角形求交,这部分对于GPU来说是不好做的,因此NVIDA设计了专门的硬件来帮助我们每秒可以trace更多的光线。
1 sample per pixel就是每个像素采样一个样本.从而得到最后的光追结果。
光路样本
至少要有四条光线才能构成一个最基本的光路:
- primary hitpoint(从camera出发打出一根光线打到的交点)-rasterization(光栅化)
- shadow ray(primary hitpoint 和光源之间连接进行light sampling并判断是否有遮挡)
- secondary ray(在Hitpoint根据材质采样出一个方向打出一根光线,他会打到一个物体上从而得到secondary hitpoint)
- secondary shadow ray(从secondary hitpoint与光源连接判断是否会被光源看到)
path tracing本身是一种蒙特卡洛积分的方法,本身会产生噪声,我们采样的样本越多,其噪声越小。
RTRT最核心的技术正是 降噪。实时光线追踪与path tracing相比,只是进行了一算法上的些简化,算法的核心思路不变,它本身的突破是由于硬件的能力提升。
即使是1spp得到的这么糟糕的结果,通过降噪我们仍然可以得到一个很棒的效果:
目标为1SSP下:
- 质量足够好( no overblur,no artifacts)
- 速度足够快(小于2ms内完成降噪操作)
很多方法在这不适用:
- Sheared filtering serise(SF,AAF,FSF,MAAF,...)Sheared方法不行
- Other offline filtering methods (IPP,BM3D,APR,...)离线方法不行
- Deep learning series(CNN,Autoencoder,...)深度学习不行
二、Industrial Sulution-temporal
首先假设整个看的场景的运动是连续的,就是camera以某种轨迹看向不同的物体,帧与帧之间有大量的连续性。
motion vector
物体在帧与帧之间是如何运动的,知道某个点在上一帧里点对应的位置。
本质上是时间上有记忆的一种复用,找某一点在不同帧上的对应关系来得到结果。
- 认为当前帧是需要去进行filtering,前一帧时已经filtering好的。
- 利用motion vector来知道当前帧某一点在上一帧的对应位置。
- 由于我们认为场景运动是连续的,所以认为shading也是连续的,上一帧得到降噪好的结果比如颜色之类的,可以在当前帧复用,相当于增加了spp,但并不是简单的上一帧1 spp+当前帧1 spp,由于是一个递归,因此上一帧也复用了上上一帧的结果,因此spp其实是很多的,可以理解为一个指数衰减,每一帧都有百分比贡献到下一帧。
G-Buffers-几何缓冲区:
在screen space我们可以得到很多的信息,可以从camera看去通过screen space生成深度图,法线图,Albedo图等,也可以存储per pixel depth,normal,世界坐标。
Back projection
通过Back projection方法求出了motion vector
frame i: 当前帧
frame i-1:上一帧
我们找的不是像素的位置,而是当前帧像素里包含的内容在上一帧哪一个像素里。当前帧(frame i)中蓝点这个像素我们所得到的点的世界坐标,投影到上一帧(frame i-1)中对应的是哪个像素。
- 一个点的世界坐标需要通过MVP矩阵和视口矩阵从而得到在screen space上的坐标,E-viewport变换,从屏幕空间到世界坐标则依次乘逆矩阵。
- 若上一帧到这一帧发生了变换,则采用逆变换。将当前帧世界坐标乘以帧移动的逆矩阵就得到了上一帧中这个点的世界坐标。
- s'为上一帧世界坐标已知,MVP和视口变换已知,可以求出上一帧屏幕坐标。
Temporal Accum./Denoising
得到了motion vector之后,我们就可以把当前帧(noisy的图)和上一帧(没有noisy的图)线性结合在一起。
- ~ : unfiltered 表示没有filter噪声挺多的内容
- - : filtered 没有噪声或者噪声比较小的
首先对当前帧进行自己的降噪,让他不那么noise,然后在时间上,使用当前帧的结果和当前帧对应的上一帧(已经降噪了的)做线性blending.其中![]() 表示平衡系数,当前帧的贡献,在(0.1-0.2)之间。
表示平衡系数,当前帧的贡献,在(0.1-0.2)之间。
时间上的降噪的过程:
- 如果在进行rasterization(primary ray)时得到了世界坐标信息的图存储在G-buffer中
- 如果没有其信息,则在当前帧的像素通过逆视口变换和逆MVP变换得到世界坐标
- 已知motion矩阵,将世界坐标逆motion得到上一帧的世界坐标
- 将上一帧的世界坐标进行正MVP变换和视口变换得到当前帧中的像素在上一帧中的屏幕位置
- 将两个值线性blending起来从而得到当前帧最后的结果
缺点:
- switching scenes (burn-in period)-突然切换场景,由于我的上一帧并没有新场景的任何信息因此得到的结果肯定不准确,或者切换光源。
- walking backwards in a hallway (screen space issue)-在倒退的时候周围的信息会不断的增多,因此我们当前帧新出现的物体无法在上一帧的屏幕空间内找到相对应的点。
- suddenly appearing background(disocclusion)-上一帧被遮挡,当前帧未被遮挡。会产生这种残影/拖尾的现象。
避免残影:
- clamping-把上一帧拉到接近当前帧的结果。
- detection-判断是否仍要使用上一帧的结果,在工业界我们渲染是认为每个物体都有自己的编号,如果编号不同,那么认为motion vector就不在靠谱了。残影现象没有了,却产生了噪声。
阴影问题
光源从左到右移动,而场景几何并不发生移动,motion vector是0,但是由于我们一直在复用未移动的帧结果,就会导致拖影的阴影出现。场景不动的情况下 motion vector为0,如果shading改变会出现错误的显示。
地板是不动的,因此其上面的每一个像素点的motion vector为0,当我们移动物体时,其地板需要一定的时间适应,之后再在地板上反射出当前场景中的物体,也就是反射滞后。
三、Implementation of filtering
Gaussian filtering
滤波Filtering:模糊操作,从一个有噪声的图得到干净的图。采用的低通滤波器只保留低频的信息,除掉高频的信息。
- 高频信息中就全是噪声吗?那么高频中不是噪声的信息被除掉会不会导致信息丢失?
- 低频信息中就没有噪声吗?
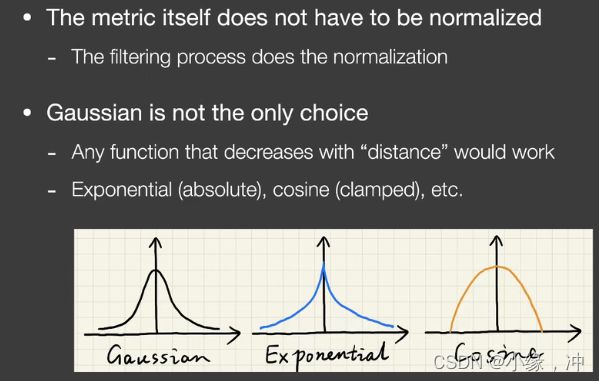
为了给光线追踪由于蒙特卡洛产生的噪声降噪时,用的是高斯的滤波器,它的滤波核为类似于正态分布,中心值高,向两边衰减:
对于任何一个中心像素i
我们需要定义 权值和(sum_of_weights),加权贡献值的和(sum_of_weighted_values)
对于中心像素i周围一圈的任意像素j(包括像素i本身)
根据像素i和像素j之间的距离和高斯的σ找对应的j贡献给i的值(权值) w_ij
将权值w_ij与像素j对应的颜色值相乘得到j的加权贡献值累加
将权值w_ij累加到sum_of_weights
进行归一化sum_of_weighted_values/sum_of_weights从而得到像素i最终的结果
- 归一化:分子是一个加权的visibility求和,分母则是权的求和也就是sum_of_weighted_values/sum_of_weights.
- 高斯的滤波核下,sum_of_weights不会为0
- 像素j输入的值i可能是一个多通道的值
Bilateral filtering-双边滤波
通过高斯我们得到了一个整体都被模糊的结果,但是我们想让边界仍然锐利,双边滤波(Bilateral filtering)将颜色变化特别剧烈的地方认为是边界。
保留边界的信息(高频):我们认为颜色变化特别剧烈的地方认为是边界,如果二者差距不是特别大我们继续用高斯处理j到i的贡献。如果像素i和像素j之间的颜色值差距过大,我们认为这两个像素分别在边界的两边,从而让像素j给i的贡献变少,就不会出现边界的模糊情况。
i和j代表一个像素,k和l代表另一个像素,前半部分为高斯滤波,如果ij之间的差距过大,则让j给i的贡献变小,I(i,j)表示第一个像素的值,I(k,l)表示第二个像素的值,他们之间的差异就是分子部分,如果差异过大,就相当于在原本的高斯核上乘上了一个指数(负距离的平方)距离差异越大,整体接近0。
通过双边滤波我们对左边的原图进行处理,可以发现山上的细节和湖面的细节被很好的模糊了,但是边界仍完美的保留了下来,这就是我们想要得到的结果,保留了低频信息但也保留了边界,但有可能分不清噪声和边界。
Joint Bilateral filtering-联合双边滤波
Gaussian filtering判断两个像素之间的绝对距离,Bilateral filtering两个像素之间的距离,和颜色之间的距离。G-BUFFER完全没有噪声,与G-buffer有关。
在RTRT中得到的结果有很明显的噪声:
如果用高斯,我们是通过两个像素之间的绝对距离找对应贡献,双边滤波的话在考虑距离的同时还会考虑两个之间的颜色变化,因为A和B都很noise,双边滤波得到的结果是不准确的。
引入深度:
从G-buffer得到各自的深度信息,我们可以看到B的深度比较浅,而A的深度比较深,所以我们不希望A有太多的贡献到B上。
引入法线:B,C二者之间的深度是差不多的,BC法线朝向是不一样的。
联合双边滤波的本质就是在kernel里多算几组不同feature下的贡献,并将其相乘得到最后的结果。
四、Implementing Large filters
滤波:对于任何一个像素,我们需要考虑他周围N * N个像素的贡献值,加权平均之后写回这个像素上。如果是large filter,也就是如果这个N * N很大,就会使得filter变得特别慢。
Separate Passes(拆分实现)
有一张图,我们先将它在水平方向上filter一遍,之后再在竖直方向上filter一遍,也就是将本来一趟N * N的,分成两趟来做,水平的1 * N和竖直的 N * 1。
如果我们使用N * N的filter,对于任何一个像素我们需要访问N^2个纹理。但如果我们将其拆分为两趟,第一趟访问N个纹理,第二趟访问N个纹理,总共访问了2N个纹理。
2D的高斯filter拆分为两个1D的高斯filter:高斯函数本身就是可拆分的
filtering == convoluation 滤波 == 卷积
Progressively Growing Sizes
我们不希望对于任何一个像素进行N * N次的纹理查询,采用一个逐步增大的filter,比如先用一个小的filter,然后用中号的filter,最后是大号的filter,通过多趟的filter得到N*N的filter得到的结果。
多趟操作,每趟都是5 * 5大小的filter,第一趟是i=0,第二趟i=1……不同趟数的5*5的filter中间是有间隔的,在第i趟时,样本之间的间隔是2^i,但每次都要采样5个。
假设要做5趟,每趟都是5 * 5的filter,那么i在第五层时候,样本之间的间隔是 2^4 = 16,第五层一共要五个样本,也就是4个间隔,大小为64。也就是说在第五层时候我们相当于做了一个64 * 64的filter,但我们对于这个像素来说,我们做了五趟,每趟5 * 5大小的filter,一共做了 125次的纹理查询,对于 64 * 64 = 4096次这个数字来说是很小。
1.为什么要逐渐增大filter,而不是一上来就使用第五趟中间间隔16个样本的filter?
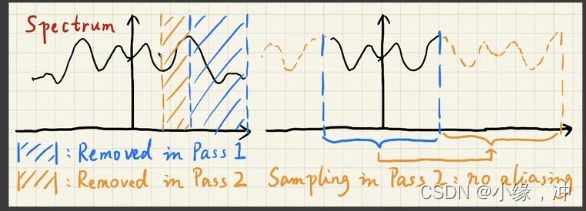
- 用更大的filter == 除掉低频信息,在第一趟时候,通过一个小范围的filter,将频谱上的高频信息(蓝色区域)除掉了,依次类推直到最后一趟除掉最低频上的信息。
2.为什么可以采样间隔那么多的样本?
- 采样 = 重复的搬移频谱,第一趟pass中出去了高频蓝色区域,然后在第二趟pass中相当于在9 * 9的filter中采样出 5*5的filter,我们采样的间隔对应到频谱上正好是右半图的蓝色部分,也就是在第一趟除掉高频信息后的区域的2倍。
五、Outlier Removal
用蒙特卡洛方法渲染一张图时,得到的结果会出现一些点过亮或者过暗,如果有一个点过亮,在经过这个7*7的filter处理过后,会影响一块区域,使得它这一块区域变亮。
Outlier Detection and Clamping
Detection:对于每个像素,我们都取他们周围一个小范围的区域,例如7*7或者5*5,然后把这个范围内颜色的均值(mean)和方差(variance)给算出来,我们认为正常的范围在均值+-若干方差内,超过这个范围的我们认为他是outlier。
Clamping:如果在范围内我们找到了outlier的点,我们把这个点的值给clamp到接近范围的值。
Temporal Clamping
当motion vector为0导致的残影现象,当前帧与上一帧中对应的信息差异过大时,我们把上一帧中的信息值给clamp到接近当前帧的信息值。
如果上一帧对应的值超出这个范围,则把他clamp到范围内,再和当前帧做线性blending,从而得到当前帧noisy-free的结果。
六、Specific Filtering Approaches for RTRT
SVGF-Basic Idea
ground truth和svgf结果非常接近,SVGF的方法与在时空上降噪的方法差不多,加了一些variance analysis和tricks.
SVGF-Joint Bilateral Filtering
Depth:
A,B侧向我们,所以深度差距比较大,按照深度来决定贡献不太合理,可以看沿着法线的那个面投影出来的深度差异。exp(x)是返回e的x次方。
深度的梯度就是往某一方向上的变化率,因此当我们知道A和B之间的距离,之后用 深度梯度 X 距离 = 实际深度变化量(垂直于平面法线上的变化 * 距离 = 实际深度变化量)
Normal:
我们用两个点法线向量求一个点积,由于求出来的值有可能是负值,因此使用max()把负的值给clamp到0。如果场景中运用了法线贴图来制造凹凸效果,我们再判断时运用平面原本的法线,而不是为了制造凹凸效果而改变过的法线。
Luminance:
在考虑颜色差异时,最简单就是应用双边滤波里给的颜色差异来考虑,比如我们将RGB转换为grayscale(灰度),这种颜色我们称其为luminance。由于噪声的存在会出现一些干扰,也就是B点虽然在阴影里,但是可能刚好选择的点是一个噪声,也就是其特别亮,此时A特别亮,B也特别亮,那么A和B就会互相贡献。
SVGF中V-variance方差:我们在考虑A点是否贡献到B点时,先看A和B点之间的颜色差异,并且除以B点周围的一个标准差。在标准差大的时候更不愿意去相信颜色差异。
B点的variance:在点的周围取一个7*7的区域算出区域里的variance,同样的操作在时间上累积下来(平均),找上一帧中对应点的variance,从而通过motion vector在temporal上把variance信息给filter下来,这样先spatial filter求出variance之后,再随时间平均从而得到了一个比较平滑的variance值。最后在使用variance时如果不放心,我们再在周围取一个3*3的区域做一次spatial filter得到variance。
spatial filter --> temporal filter --> spatial filter
SVGF会产生“残影“现象:当一个场景固定,我们只移动光源时候,阴影会随着光源的移动而变化,当前帧会复用上一帧的阴影。
七、RAE(Recurrent AutoEncoder)
- 一种结构,对Monte carlo路径追踪得到的结果进行reconstruction-对RTRT做滤波。
- 后期处理,把noise的图变clean。
- 使用G-buffers
- 神经网络会自动将temporal的结果累积起来
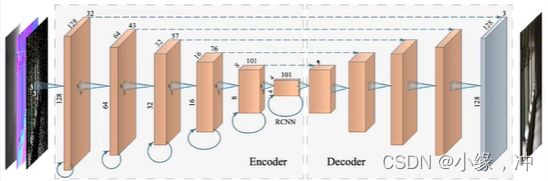
AutoEncoder,是一个漏斗形的结构,输入经过若干层神经网络后变成一个很小的东西,之后再将小的东西不断地展开,类U型神经网络。
AutoEncoder
每一层都有连向他自己的。可以利用历史的信息,每一层神经网络有一个recurrent连接,也就是每一层神经网络不仅可以连向下一层,也可以连回自己这一层。-从之前的帧中积累(并逐渐忘记)信息
Comparison