水平集图像分割并行加速算法设计与实现(串行、OpenMP、CUDA)——串行实现篇

本次水平集图像分割并行加速算法设计与实现包含：原理篇、串行实现篇、OpenMP并行实现篇与CUDA GPU并行实现篇四个部分。
原理篇主要讲解水平集图像分割的原理与背景。串行实现篇、OpenMP并行实现篇与CUDA GPU并行实现篇主要基于C++与OpenCV实现相应的图像分割与并行加速任务。本系列属于图像处理与并行程序设计结合类文章，希望对你有帮助。

串行基本流程设计

水平集图像分割串行代码设计流程如上图所示。演化开始前需要首先对原始图片进行导入，并对原始图片相关变量进行初始化，其后根据选定初始化轮廓区域结合符号距离函数进行水平集的初始化。在上述完成后，水平集演化过程开始，根据相应数据依赖关系，首先需要完成对应Heaviside函数、Dirac函数与曲率的计算，其后根据Heaviside函数计算结果对前景与背景均值进行计算。
接着便可将上述计算结果代入式(1)进行演化模拟。具体水平集图像分割与演化原理，见本人之前发布的原理篇所示。
$$\begin{array}{c}{\varphi }_{i,j}^{n+1}=L\left({\varphi }_{i,j}^n\right)\Delta t+{\varphi }_{i,j}^n\end{array}\text{\hspace{1em}(1)}$$
最后对水平集的收敛性进行判断，当零水平集所对应轮廓收敛时，则程序结束退出，反之，继续迭代进行演化。

主要模块编程实现设计

原始图片初始化模块

原始图片初始化模块主要用于对原始图片相关变量进行初始化。其会将原始图片转化为单通道的灰度图像，并根据原始图像尺寸对水平集矩阵、Heaviside函数矩阵等相关数据进行初始化，具体代码如下所示：

LevelSet::LevelSet(const Mat& src)
{
	if (src.channels() == 3)
	{
		cvtColor(src, src_, COLOR_BGR2GRAY);
		src.copyTo(image_);
	}
	else
	{
		src.copyTo(src_);
		cvtColor(src, image_, COLOR_GRAY2BGR);
	}
	src_.convertTo(src_, CV_32FC1);
	phi_ = Mat::zeros(src_.size(), CV_32FC1);
	dirac_ = Mat::zeros(src_.size(), CV_32FC1);
	heaviside_ = Mat::zeros(src_.size(), CV_32FC1);
}

水平集初始化模块

根据CV水平集模型，采用倒置的符号距离函数进行水平集的初始化，具体倒置符号距离函数公式如式(2)所示。
$$\begin{array}{c}\varphi (\mathrm{x})=\{\begin{array}{cc}-\mathrm{dist}(\mathrm{x},C)& \text{ if }\mathrm{x}\text{ is outside }C\\ 0& \mathrm{x}\in C\\ \mathrm{dist}(\mathrm{x},C)& \text{ if }\mathrm{x}\text{ is inside }C\end{array}\end{array}\text{\hspace{1em}(2)}$$
其中dist(x,C)表示点x到轮廓C上所有点的最短距离，具体转化示例见下图所示。

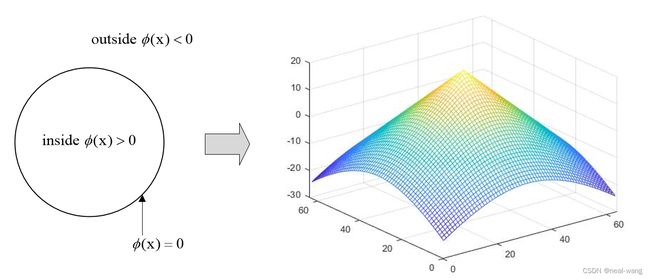
根据上图可知，其将二维平面的轮廓曲线作为零水平集（水平集曲面与z=0平面的交面），转化为一个三维水平集曲面，通过三维曲面的演化来模拟二维的轮廓演化。（当迭代收敛后直接获取对应水平集曲面的零水平集，即为分割完成后区域的轮廓）
具体水平集初始化代码如下所示：

// 初始化水平集
void LevelSet::initializePhi(Point2f center, float radius)
{
	const float c = 2.0f;
	float value = 0.0;
	for (int i = 0; i < src_.rows; i++)
	{
		for (int j = 0; j < src_.cols; j++)
		{
			value = -sqrt(pow((j - center.x), 2) + pow((i - center.y), 2)) + radius;
			if (abs(value) < 1e-3)
			{
				//在零水平集曲线上
				phi_.at<float>(i, j) = 0;
			}
			else
			{
				// 在零水平集内：为正
				// 在零水平集外：为负
				phi_.at<float>(i, j) = value;
			}

		}
	}
}

曲率模块

曲率模块主要用于对曲率进行计算。其中曲面的曲率可以运用梯度除以其模值的散度进行计算，具体计算公式为式(3)所示：
$$\begin{array}{c}{\text{ curvature }}_{ij}=\mathrm{div}\left(\frac{\nabla \varphi }{|\nabla \varphi |}\right)\end{array}\text{\hspace{1em}(3)}$$
其具体实现代码如下所示：

//  计算曲率
void LevelSet::calculateCurvature()
{
	Mat dx, dy;
	// 计算一阶梯度
	gradient(src_, dx, dy);
	Mat norm = Mat::zeros(src_.size(), CV_32FC1);
	// 计算模值
	for (int i = 0; i < src_.rows; i++)
	{
		for (int j = 0; j < src_.cols; j++)
		{
			norm.at<float>(i, j) = pow(dx.at<float>(i, j) * dx.at<float>(i, j) + dy.at<float>(i, j) * dy.at<float>(i, j), 0.5);
		}
	}
	Mat dxx, dxy, dyx, dyy;
	// 二阶梯度与散度计算
	gradient(dx / norm, dxx, dxy);
	gradient(dy / norm, dyx, dyy);
	curv_ = dxx + dyy;
}

上述gradient函数用于计算对应矩阵x方向与y方向的梯度，具体可参见本人github仓库源码。

前景背景均值模块

前景背景均值模块用于对轮廓所划分的前景与背景均值进行计算，其将调用Heaviside函数计算结果对前景和背景范围进行划分，具体代码如下所示：

// 计算像素点前景与背景均值
void LevelSet::calculatC()
{
	c1_ = 0.0f;
	c2_ = 0.0f;
	float sum1 = 0.0f;
	float h1 = 0.0f;
	float sum2 = 0.0f;
	float h2 = 0.0f;
	float value = 0.0f;
	float h = 0.0f;
	for (int i = 0; i < src_.rows; i++)
	{
		for (int j = 0; j < src_.cols; j++)
		{
			value = src_.at<float>(i, j);
			h = heaviside_.at<float>(i, j);

			h1 += h;
			sum1 += h * value;
			h2 += (1 - h);
			sum2 += (1 - h) * value;
		}
	}
	c1_ = forntpro_ * sum1 / (h1 + 1e-10);
	c2_ = sum2 / (h2 + 1e-10);
}

同时为了更好的对图像进行分割，为前景均值添加权重项forntpro_，以此可根据不同情况对分割结果进行优化。

演化模拟与收敛性判定模块

在上述模块运行完毕后，可对水平集进行迭代演化。当演化后轮廓所包含前景区域与演化前轮廓所包含前景区域相同时(水平集函数大于0的区域没有变化)，则判定水平集已经收敛，可以停止迭代跳出循环，具体代码如下所示：

// 具体演化函数
// 运用迭代法解偏微分方程，求解φ对应时间间隔的变化量
int LevelSet::evolving()
{
	showEvolving();
	showLevelsetEvolving();
	// 迭代次数
	int k;
	bool flag; //是否收敛判定标识
	for (k = 0; k < iterationnum_; k++)
	{
		clock_t begin, end; // 计时变量
		begin = clock();
		flag = false;
		heaviside();
		dirac();
		calculatC();
		calculateCurvature();
		//update phi
		// 模拟演化过程
		for (int i = 0; i < src_.rows; i++)
		{
			for (int j = 0; j < src_.cols; j++)
			{
				float curv = curv_.at<float>(i, j);
				float dirac = dirac_.at<float>(i, j);
				float u0 = src_.at<float>(i, j);
				// 能量函数中各项计算
				float lengthTerm = mu_ * dirac * curv;
				float areamterm = nu_ * dirac;
				float fittingterm = dirac * (-lambda1_ * pow(u0 - c1_, 2) + lambda2_ * pow(u0 - c2_, 2));
				float term = lengthTerm + areamterm + fittingterm;
				float phinew = phi_.at<float>(i, j) + timestep_ * term;
				float phiold = phi_.at<float>(i, j);
				phi_.at<float>(i, j) = phinew;

				if (!flag)
				{
					if (phinew * phiold < 0)
					{
						flag = true;
					}
				}

			}
		}
		showEvolving();
		showLevelsetEvolving();
		// 对是否收敛进行判断
		if (!flag)
		{
			break;
		}
		end = clock();
	}
	showEvolving();
	showLevelsetEvolving();
	return k;
}

其中showEvolving()函数用于绘制演化过程中的零水平集轮廓，showLevelsetEvolving()用于绘制水平集函数对应的色温图。
上述仅仅展现部分主要代码，详细代码见本人github仓库所示，具体链接如下 。
水平集图像分割算法串行与并行代码以及相关测试用例

测试用例说明

本次串行水平集程序的测试用例主要来源于实际生活中存在，或虚拟应用场景中存在的图形图像。

实际存在图片用例

为更加精准测试算法性能，针对实际存在实物方面，选取人脸嘴唇图片作为测试用例，其尺寸为883像素*594像素，具体如下图所示。

在上图中，包含皮肤斑纹、嘴唇反光等噪声，并含有不规则边缘，利于对算法的图像分割效果进行测试。其水平集的初始化区域选择为一个以点(400,240)为圆心，半径为200的圆，具体如下图所示。

虚拟业务场景图片用例

针对虚拟业务场景方面，本项目选取两张飞机游戏图片作为测试用例，其中飞机游戏图片一尺寸为320像素*570像素，飞机游戏图片二尺寸为476像素*752像素，具体如下面两图所示。

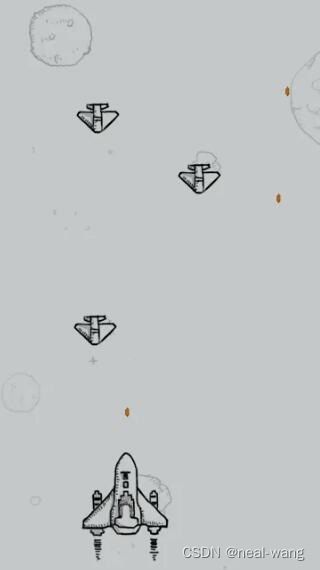
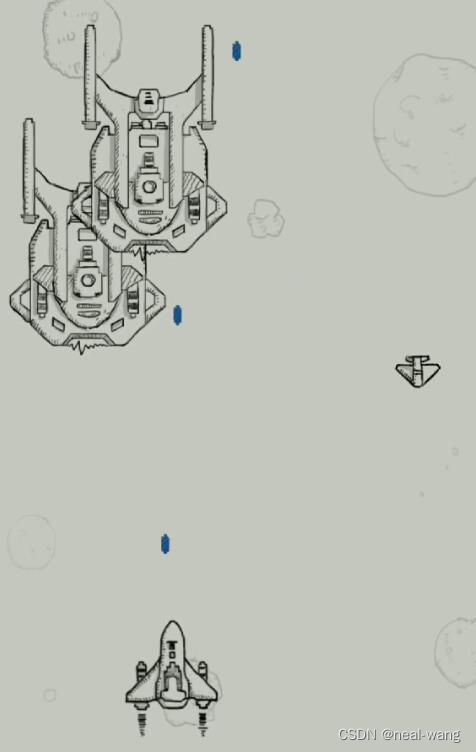
两幅图像具有不同背景与图像特征，利于测试算法针对不同分割对象的通用性。同时其中均含有浅色背景噪声（星球、陨石等），有利于对算法的分割效果进行更加精准的评估。
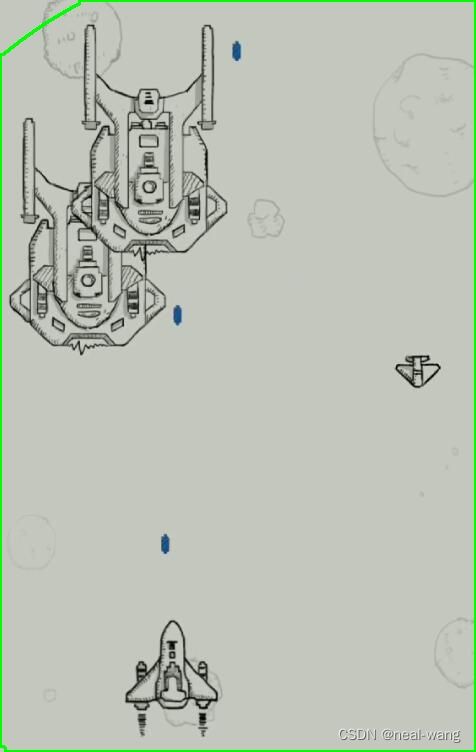
其均选择近乎全图作为水平集初始化区域。同时为进一步对模型通用进行测试，在飞机游戏图片一中，初始化区域不包含图片边缘四角，而在飞机大战图片二中，其包含图片边缘中的三个角，具体如下面两图所示。

运行环境说明

硬件运行环境

CPU：Intel® Core™ i5-9300H 4核CPU处理器

GPU：NVIDIA GeForce GTX 1050显卡

软件运行环境

OpenCV: v4.5.0

CUDA: v11.0

运行结果展示

针对人脸嘴唇图片，以时间步长为1进行测试，最大迭代次数为1000，得到的测试过程与结果展示如下图所示。

针对飞机游戏图片一，以时间步长为5进行测试，最大迭代次数为1000，得到的测试过程与结果展示如下所示。

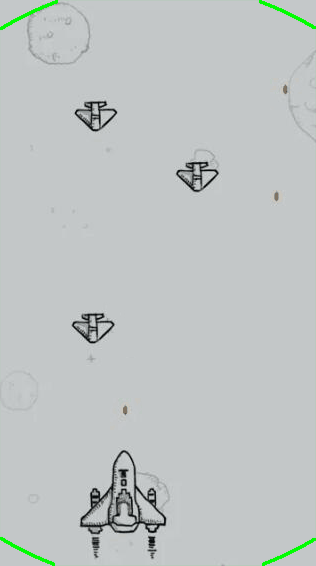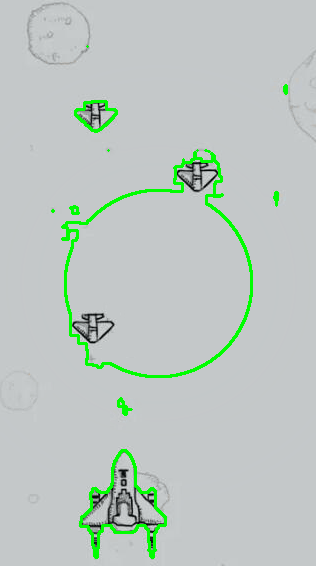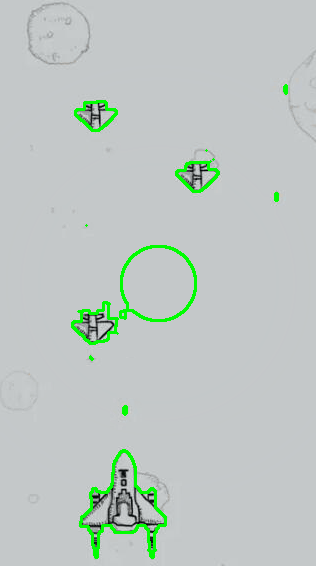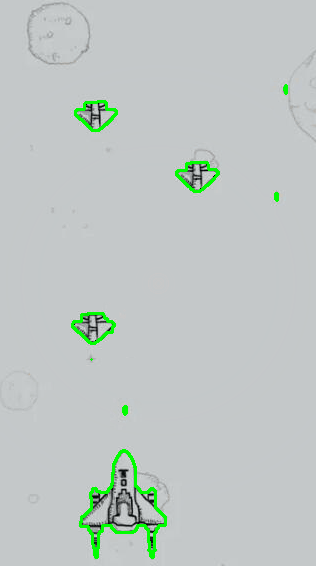
针对飞机游戏图片二，同样以时间步长为5进行测试，最大迭代次数为1000，得到的测试过程与结果展示如下所示。

上图由于gif大小限制，仅仅展示演化过程开头部分，完整过程可根据所提供代码自行运行得到。
其左侧图为对应的水平集演化色温图，深蓝色表示小于零的背景，其他颜色表示大于零部分的水平集区域，从该图中可以大致观察到水平集函数的形态与收敛过程。其右侧为对应的演化轮廓曲线（零水平集）。
从上述测试用例分割结果可以看出，水平集图像分割算法可以实现对所需目标前景的精准分割。同时其也对待分割图像中的噪声具有一定的鲁棒性。
对上述测试用例进行性能分析，分别取各图片十次运行时间进行平均，得到测试用例串行时间表，具体如下表所示：

图片名称	人脸嘴唇	飞机游戏一	飞机游戏二
串行时间(ms)	342158	34750	220024

从上表中的运行时间可以看出，水平集图像分割虽然可以得到较好的分割效果，但演化时间较长，针对上述人脸嘴唇图片需要接近6分钟才可完成分割任务，极大的限制了该算法的应用，由此对应并行加速算法的设计具有一定的现实意义。

下期将对水平集图像分割OpenMP并行加速算法的设计与实现进行讲解。