【AI】反向传播的基本原理(06)
目录
1、有个小印象
2、易混淆的函数
3、反向传播概念
4、图解反向传播算法
4.1、三层神经网络
4.2、前向传播过程
4.3、计算误差
4.4、反向传播算快速法修正W
5、链式求导法则
6、梯度下降修正W
7、举例推导
1、有个小印象
个人感觉反向传播代码实现虽然很简单,但是他的原理其实还是需要花点时间理解的,从游戏视角中理解前向和反向传播原理如下:
1)前向传播:三个人在玩你画我猜的游戏,然后第一个人给第二个人描述,再将信息传递给第三个人,由第三个人说出画的到底是啥。
2)反向传播:第三个人得知自己说的和真实答案之间的误差后,发现他们在传递时的问题差在哪里,向前面一个人说下次描述的时候怎样可以更加准确的传递信息。就这样一直向前一个人告知。
3)三个人之间的的默契一直在磨合,然后描述的更加准确。
2、易混淆的函数
损失函数:是定义在单个样本上的,算的是一个样本的误差。
代价函数:是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。
目标函数:是最终需要优化的函数。等于也就是代价函数 + 正则化项。(正则化:一种防止过拟合的方法)。
3、反向传播概念
反向传播,和前向传播比更复杂,但是他是神经网络能够学习的关键,她能够调整神经网络的参数,能让神经网络预测的更准。神经网络前向传播就是输入数据,通过一层层的传播,会输出一个输出信号,也就是预测值,他会和真实值比较,如果相近,就预测的准,如果偏差大,就预测的不准。
那预测值和真实值的差别,除了评价预测好坏以外,能不能用来调整神经网络中的的参数,是可以吗?这个利用偏差值调整参数的过程就是,反向传播。
反向传播,也叫误差反传,用误差修正网络中的参数,修正的是权重参数、偏置参数。神经网络就是看你权重和偏置准不准,如果准,预测结果就好些。神经网络的中心任务,就是找到权重、偏置的值,那我们应该怎么找呢
官方的叫法:反向传播(英语:Backpropagation,缩写为BP)是“误差反向传播”的简称,是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。(误差的反向传播)。
4、图解反向传播算法
如果去问一下了解BP算法的人“BP算法怎推导?”,大概率得到的回答是“不就是链式求导法则嘛”,我觉得这种答案对于提问题的人来说没有任何帮助。BP的推导需要链式求导不错,但提问者往往想得到的是直观的回答,毕竟理解才是王道。最形象的理解,还是画图。首先拿一个简单的三层神经网络来举例,如下:
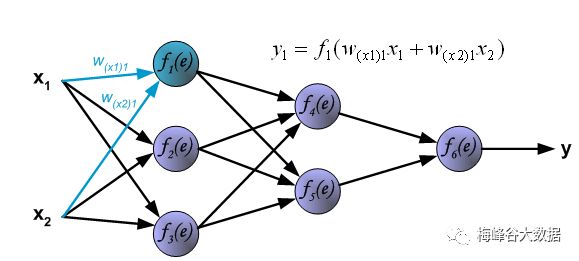
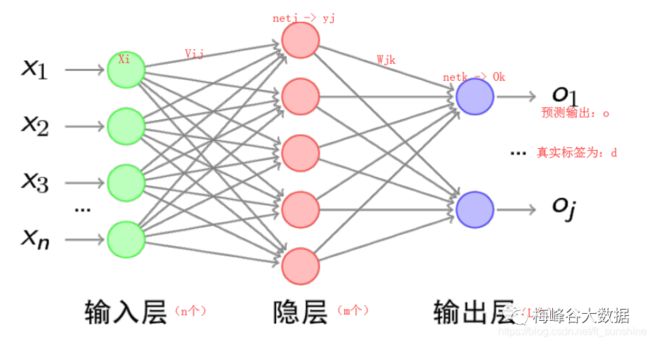
4.1、三层神经网络
每个神经元由两部分组成,第一部分(e)是输入值和权重系数乘积的和,第二部分(f(e))是一个激活函数(非线性函数)的输出, y=f(e)即为某个神经元的输出,如下:
4.2、前向传播过程
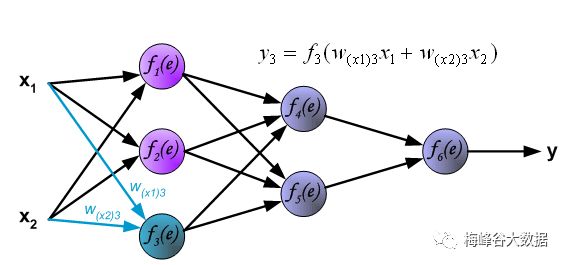
第一层计算
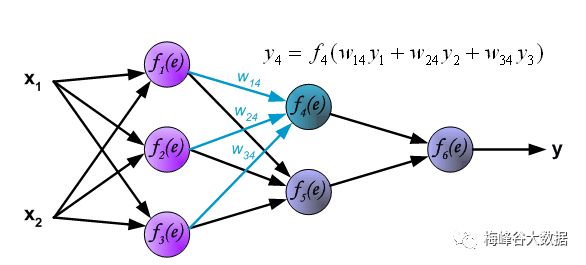
第二层计算
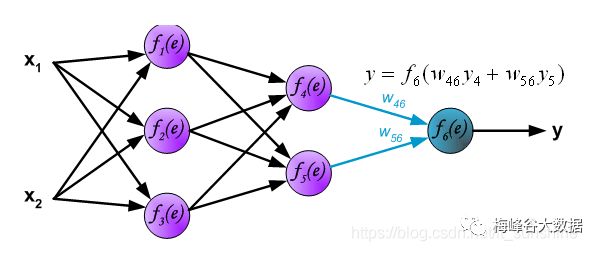
第三层计算
到这里为止,神经网络的前向传播已经完成,最后输出的y就是本次前向传播神经网络计算出来的结果(预测结果)
4.3、计算误差
这个预测结果不一定是正确的,要和真实的标签(z)相比较,计算预测结果和真实标签的误差(δ \deltaδ),如下:
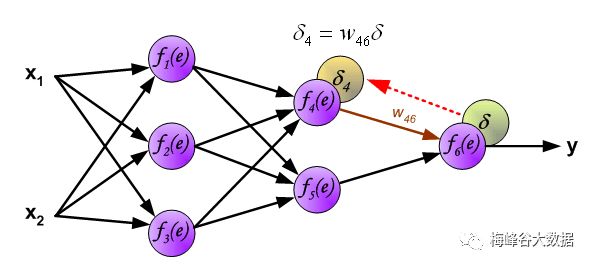
计算第三层误差
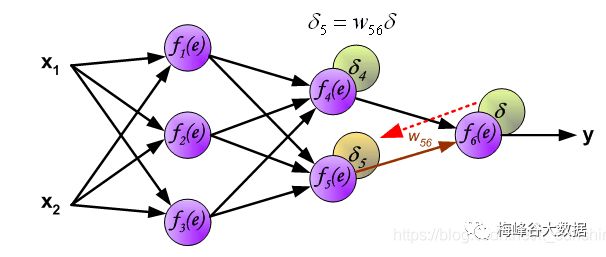
计算导数第二层误差
下面开始计算每个神经元的误差(δ \deltaδ):
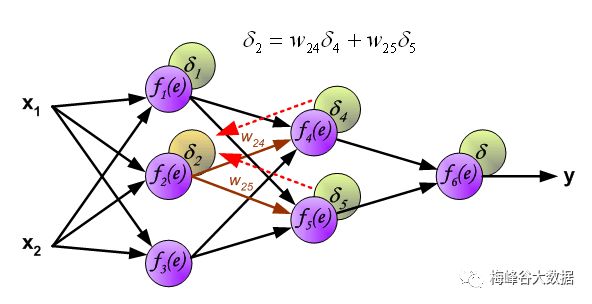
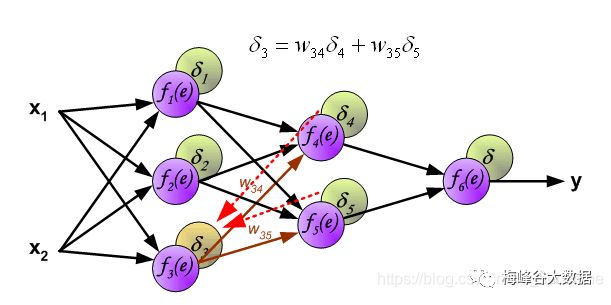
计算第一层误差
计算第一层神经元导致的误差 If propagated errors came from few neurons they are added. The illustration is below:
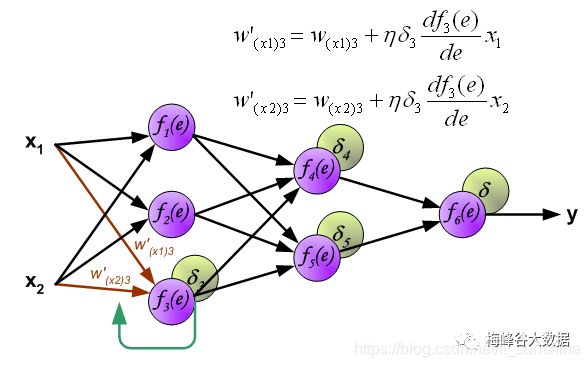
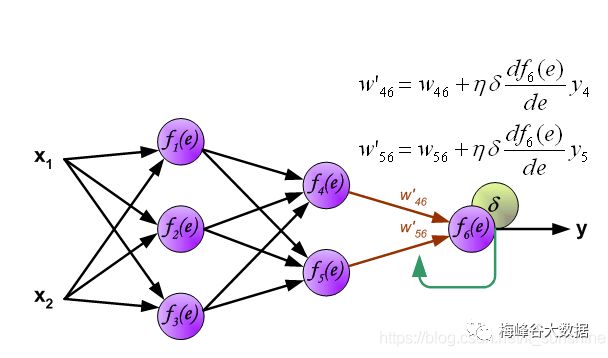
4.4、反向传播算快速法修正W
至此,每个神经元的误差都可以计算出来,下面开始利用反向传播的误差,计算各个神经元(权重)的导数,开始反向传播修改权重。
第二层网络的权重参数修正
最后一层权重修正
系数η(原文为eta)影响网络学习的速度。有几种技术可以选择这个参数。第一种方法是以大参数值开始学习过程。在建立权重系数的同时,参数逐渐减少。第二种更复杂的方法是以小参数值开始学习。在学习过程中,参数在学习提前时增加,然后在最后阶段再次降低。以低参数值开始教学过程可以确定加权系数符号
5、链式求导法则
首先明确,“正向传播”求损失,“反向传播”回传误差。同时,神经网络每层的每个神经元都可以根据误差信号修正每层的权重,只要能明确上面两点,那么下面的例子,只要会一点链式求导规则,就一定能看懂!
上图的前向传播(网络输出计算)过程如下:(此处为网络的整个误差的计算,误差E计算方法为mse)
上面的计算过程并不难,只要耐心一步步的拆开式子,逐渐分解即可。现在还有两个问题需要解决:
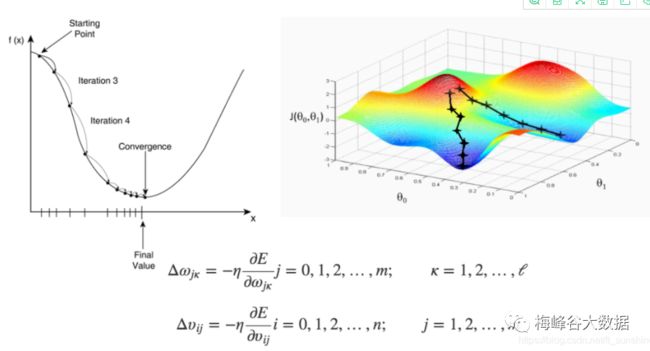
6、梯度下降修正W
第4个模块讲解了,可以通过误差不断的来修正,这样反反复复的去试,要经过很多轮的试错才能找到最佳的W。如何用最快速的方法来找到最佳W呢,答案是梯度下降算法,原理上一篇博客已经讲解。
·误差E有了,怎么调整权重让误差不断减小?
·E是权重w的函数,何如找到使得函数值最小的w。
解决上面问题的方法是梯度下降算法(简单图示如下),大家如有不太懂的可先行查阅别的资料,只要能达到理解线性回归梯度下降算法的水平即可,这里不再赘述。
解决上面问题的方法是梯度下降算法(简单图示如下)
7、举例推导
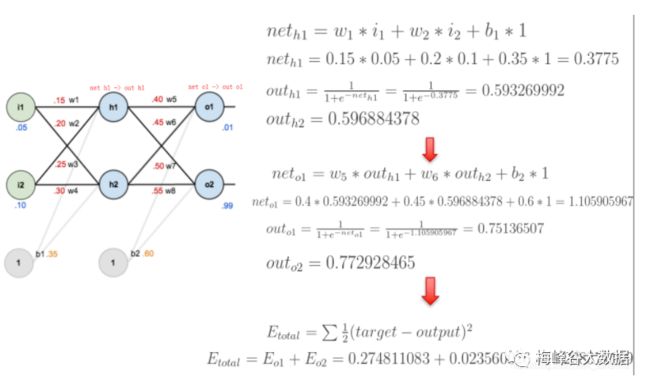
就算上面的所有东西你都看的迷迷糊糊,通过下面的例子,相信绝大多数人也能很轻松的理解BP算法。如图是一个简单的神经网络用来举例:
下面是前向(前馈)运算(激活函数为sigmoid):
下面是反向传播(求网络误差对各个权重参数的梯度):
我们先来求最简单的,求误差E对w5的导数。首先明确这是一个“链式求导”过程,要求误差E对w5的导数,需要先求误差E对out o1的导数,再求out o1对net o1的导数,最后再求net o1对w5的导数,经过这个链式法则,我们就可以求出误差E对w5的导数(偏导),如下图所示:
导数(梯度)已经计算出来了,下面就是反向传播与参数更新过程:
如果要想求误差E对w1的导数,误差E对w1的求导路径不止一条,这会稍微复杂一点,但换汤不换药,计算过程如下所示:
至此,“反向传播算法”及公式推导的过程总算是讲完了
以上雄文参主要来自CSDN博文,并加以整理,更多AI文章请关注