深度优先搜索（DFS）与广度优先搜索（BFS）算法详解

深度优先搜索（DFS）与广度优先搜索（BFS）详解

1.广度优先搜索算法

1.1.前言

和树的遍历类似，图的遍历也是从图中某点出发，然后按照某种方法对图中所有顶点进行访问，且仅访问一次。

但是图的遍历相对树而言要更为复杂。因为图中的任意顶点都可能与其他顶点相邻，所以在图的遍历中必须记录已被访问的顶点，避免重复访问。

根据搜索路径的不同，我们可以将遍历图的方法分为两种：广度优先搜索和深度优先搜索。

1.2.图及图的遍历

概念：

线性表和树两类数据结构，线性表中的元素是“一对一”的关系，树中的元素是“一对多”的关系，本章所述的图结构中的元素则是“多对多”的关系。图（Graph）是一种复杂的非线性结构，在图结构中，每个元素都可以有零个或多个前驱，也可以有零个或多个后继，也就是说，元素之间的关系是任意的。

图的遍历：

图的遍历是指从图中的某一顶点出发，按照某种搜索方法沿着图中的边对图中的所有顶点访问一次且仅访问一次。

1.3.定义

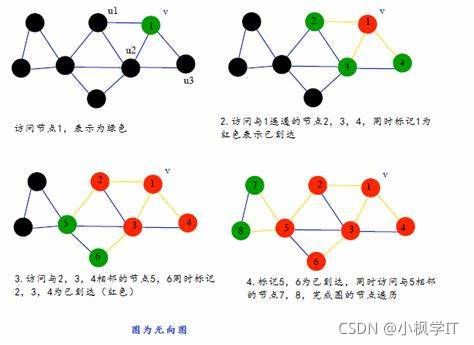
广度优先搜索算法类似于二叉树的层序遍历，是一种分层的查找过程，每向前一步可能访问一批顶点，没有回退的情况，因此不是一个递归的算法。首先访问起始顶点v，接着由v出发，依存访问v的各个未访问过的邻接顶点w1，w2，…，wi，然后依次访问w1，w2，…，wi的所有未被访问过的邻接顶点；再从这些访问过的顶点出发，访问它们所有未被访问过的邻接顶点······依次类推，直到图中所有顶点都被访问过为止。

1.4.算法图解

思路详解：

1. 以节点1为起始顶点，开始访问
2. 接着由v开始出发，依次次访问v的各个未访问过的邻接顶点$w1,w2,...,wi$，
3. 然后依次访问$w1,w2,...,wi$的所有未被访问的邻接顶点；
4. 然后再从这些访问过的顶点出发，访问它们所有未被访问过的邻接顶点
5. 直到所有顶点都被访问过为止；
6. 如果此时图中尚有顶点未被访问，则另选图中一个未被访问过的顶点作为起始点，重复上述过程，直到图中所有顶点都被访问为止；

广度优先搜索算法类似于二叉树的层序遍历，是一种分层的查找过程，每向前一步可能访问一批顶点，没有回退的情况，因此不是一个递归的算法。

性能分析：

空间复杂度：

无论是邻接表还是邻接矩阵的存储方式，BFS算法都需要借助一个辅助队列Q，n个顶点均需入队一次，在最坏的情况下，空间复杂度为$O(|V|)$。

时间复杂度：

• 邻接表：采用邻接表存储方式时，每个顶点均需搜索一次（或入队一次），故时间复杂度为$O(|V|)$，在搜索任意顶点的邻接点事每条边至少访问一次，故时间复杂度为$O(|E|)$，算法的总时间复杂度为$O(|V|+|E|)$。
• 邻接矩阵：采用邻接矩阵存储方式时，查找每个顶点的邻接点所需的时间为$O(|V|)$，故算法总的时间复杂度为$O(|V^2|)$。

1.5.代码实现：

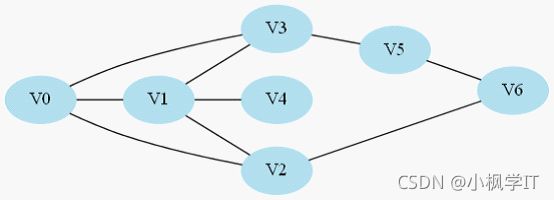
使用广度优先搜索遍历下图：

/**
 * @ClassName BFS
 * @Author Fenglin Cai
 * @Date 2021 09 30 19
 * @Description 图的广度优先搜索算法
 **/
import com.sun.istack.internal.NotNull;

import java.util.*;
//如同二叉树的层次遍历
public class BFS {

    public static class Node implements Comparable<Node> {

        private String name;

        private TreeSet<Node> set = new TreeSet<>();//有序的集合

        public Node() {
        }

        public Node(String name) {
            this.name = name;
        }

        public String getName() {
            return name;
        }

        public void setName(String name) {
            this.name = name;
        }

        public Set<Node> getSet() {
            return set;
        }

        public void setSet(TreeSet<Node> set) {
            this.set = set;
        }

        @Override
        public int compareTo(@NotNull Node o) {//排序规则
            if(name.hashCode()>o.getName().hashCode()) {
                return 1;
            }
            return 0;
        }
    }

    public Node init() {//初始化一个图及其节点
        Node nodeA = new Node("A");
        Node nodeB = new Node("B");
        Node nodeC = new Node("C");
        Node nodeD = new Node("D");
        Node nodeE = new Node("E");
        Node nodeF = new Node("F");
        Node nodeG = new Node("G");
        Node nodeH = new Node("H");
        nodeA.getSet().add(nodeB);
        nodeA.getSet().add(nodeC);
        nodeB.getSet().add(nodeD);
        nodeB.getSet().add(nodeE);
        nodeC.getSet().add(nodeF);
        nodeC.getSet().add(nodeG);
        nodeD.getSet().add(nodeH);
        nodeE.getSet().add(nodeH);
        return nodeA;
    }

    public void visite(Node node) {//访问每个节点

        System.out.print(node.getName()+" ");

    }

    public void bfs(Node start) {
        Queue<Node> queue = new LinkedList<>();//存储访问的节点

        Queue<Node> visite = new LinkedList<>();//存储访问过得节点

        queue.add(start);//起始节点添加到队列

        visite.add(start);//标识为访问过
        while (!queue.isEmpty()) {

            Node node = queue.poll();//队列头结点出队

            visite(node);

            Set<Node> set = node.getSet();//获取所有的直接关联的节点

            Iterator<Node> iterator = set.iterator();

            while(iterator.hasNext()) {

                Node next = iterator.next();

                if (!visite.contains(next)) {//不包含说明没有没有被访问

                    queue.add(next);

                    visite.add(next);
                }

            }
        }
    }

    public static void main(String[] args) {

        BFS bfs = new BFS();

        bfs.bfs(bfs.init());
    }
}

2.深度优先搜索算法

2.1.定义

与广度优先搜索不同，深度优先搜索（Depth-First-Search，DFS）类似于树的先序遍历。

思想：从一个顶点V0开始，沿着一条路一直走到底，如果发现不能到达目标解，那就返回到上一个节点，然后从另一条路开始走到底，直到所有顶点被全部走完，这种尽量往深处走的概念即是深度优先的概念。

实例：

假设按照以下的顺序来搜索：

1.V0->V1->V4，此时到底尽头，仍然到不了V6，于是原路返回到V1去搜索其他路径；

2.返回到V1后既搜索V2，于是搜索路径是V0->V1->V2->V6,，找到目标节点，返回有解。

这样就搜索到了目标节点，当然这里在可以选择多个节点时，随意选择任一节点，如果走到V1节点选择V3的话，走的路径就是

V0->V1->V3->V5->V6->V2。

2.2.算法图解

思路图解：

思路如下所示：

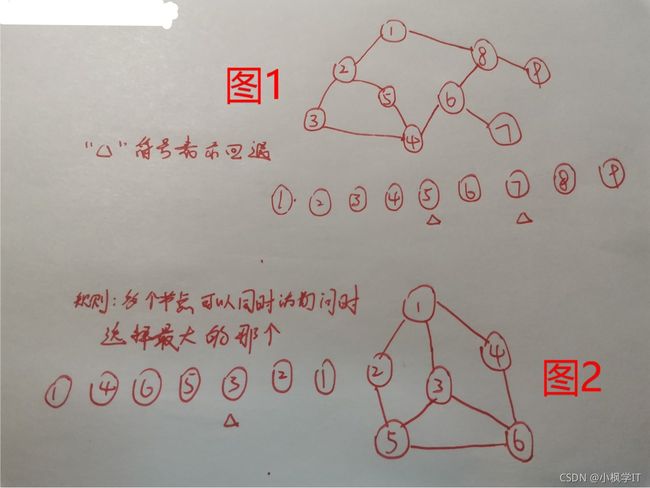
图1：

根据深度优先搜索算法的思想，且在一个节点访问下一个节点有多个选择时选最小的规则下,路径就如图中给出所示，

1. 从起始点节点1开始走，走过的路径：1->2->3->4->5
2. 在走到第5个节点时因为节点2已经走过，所以无路可走了，然后回退到节点4，再走节点6，路径：1->2->3->4->5->4->6
3. 到节点7时同样无路可走，回退到上一节点并继续走，路径：1->2->3->4->5->4->6->7->6->8->9

图2：

1. 按照图2所给的规则来，从起始节点1开始走1->4->6->5->3
2. 到节点3时因为节点1和节点6都已经走过，所以无路可走，回退到上一节点5，继续走1->4->6->5->3->5->2，

这样就遍历完了，搜索时，只需加个条件判断即可，满足条件直接跳出搜索。

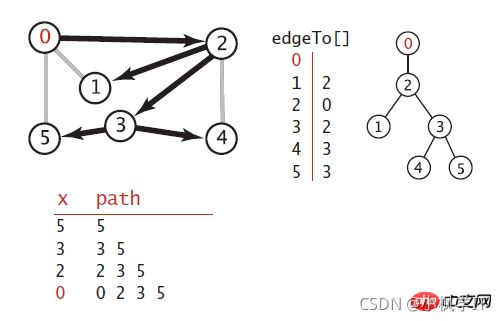
有向图转换为最小生成树

性能分析：

空间复杂度：

DFS算法是一个递归算法，需要借助一个递归工作栈，故其空闲复杂度为$O(|V|)$.

时间复杂度：

遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间取决于所用的存储结构。

• 邻接矩阵：查找每个顶点的邻接点所需的时间为$O(|V|)$，故总的时间复杂度为$O(|V{|}^2)$。
• 邻接表：查找所有顶点的邻接点所需的时间为$O(|E|)$，访问顶点所需的时间为$O(|V|)$，此时，总的时间复杂度为$O(|V|+|E|)$。

2.3.代码实现

题目描述

题目：图1是一个城堡的地形图。请你编写一个程序，计算城堡一共有多少房间（相通的所有方块为一个房间），最大的房间有多大。城堡被分割成m*n(m≤50，r≤50)个方块，每个方块可以有0~4面墙。
输入

程序从标准输入设备读入数据。第一行是两个整数，分别是南北向、东西向的方块数。在接下来的输入行里，每个方块用一个数字(0≤p≤50)描述。用一个数字表示方块周围的墙，1表示西墙，2表示北墙，4表示东墙，8表示南墙。每个方块用代表其周围墙的数字之和表示。城堡的内墙被计算两次，方块(1,1)的南墙同时也是方块(2,1)的北墙。输入的数据保证城堡至少有两个房间。

输出

城堡的房间数、城堡中最大房间所包括的方块数。结果显示在标准输出设备上。

样例输入

4
7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12 13

样例输出

5 9

思路：
要想找到一个房间，就要遍历与这个房间相关联的每一个方块，假如方块1与方块2相同，方块2与方块3、方块4相同，方块1、2、3、4构成一份房间，那我们就要遍历每一个方块以求出房间大小。在遍历的时候还要标记当前方块，以便当前方块再次被遍历。

代码实现

如下：

#include
#include
using namespace std;
 
int R, C;  //行数和列数
int color[60][60];   //用来标记当前房间是否访问过
int room[60][60];
int maxRoomArea = 0;   //用来记录面积最大的房间
int roomNumber = 0;    //房间数量
int roomArea;      //用来记录房间的面积
 
void dfs(int i, int k)
{
	if (color[i][k])
	{
		return;
	}
	roomArea++;    //房间的面积
	color[i][k] = roomNumber; //标记当前结点，防止再次遍历该节点
 
	//选择与当前结点相关联的另一个节点，继续dfs
	if ((room[i][k] & 1) == 0)dfs(i, k - 1);    //向西
	
	if ((room[i][k] & 2) == 0)dfs(i - 1, k);    //向北
	
	if ((room[i][k] & 4) == 0)dfs(i, k + 1);    //向东
	
	if ((room[i][k] & 8) == 0)dfs(i + 1, k);    //向南
	
}
 
int main()
{
	cin >> R >> C;
	for (int i = 1; i <= R; i++) {
		for (int j = 1; j <= C; j++) {
			cin >> room[i][j];
		}
	}
	memset(color, 0, sizeof(color));   //初始化
	for (int i = 1; i <= R; i++) {
		for (int j = 1; j <= C; j++) {
			if (!color[i][j]) {    //当 当前结点没有被遍历过时
				roomArea = 0;
				roomNumber++;
				dfs(i, j);
				maxRoomArea = max(roomArea, maxRoomArea);
			}
		}
	}
	cout << roomNumber << endl;
	cout << maxRoomArea << endl;
 
	system("pause");
	return 0;
}

3.深搜与广搜的比较

3.1.深度优先搜索的特点

1. 无论问题的内容和性质以及求解要求如何不同，它们的程序结构都是相同的，即都是深度优先算法（一）和深度优先算法（二）中描述的算法结构，不相同的仅仅是存储结点数据结构和产生规则以及输出要求。
2. 深度优先搜索法有递归以及非递归两种设计方法。一般的，当搜索深度较小、问题递归方式比较明显时，用递归方法设计好，它可以使得程序结构更简捷易懂。当搜索深度较大时，当数据量较大时，由于系统堆栈容量的限制，递归容易产生溢出，用非递归方法设计比较好。
3. 深度优先搜索方法有广义和狭义两种理解。广义的理解是，只要最新产生的结点（即深度最大的结点）先进行扩展的方法，就称为深度优先搜索方法。在这种理解情况下，深度优先搜索算法有全部保留和不全部保留产生的结点的两种情况。而狭义的理解是，仅仅只保留全部产生结点的算法。本书取前一种广义的理解。不保留全部结点的算法属于一般的回溯算法范畴。保留全部结点的算法，实际上是在数据库中产生一个结点之间的搜索树，因此也属于图搜索算法的范畴。
4. 不保留全部结点的深度优先搜索法，由于把扩展望的结点从数据库中弹出删除，这样，一般在数据库中存储的结点数就是深度值，因此它占用的空间较少，所以，当搜索树的结点较多，用其他方法易产生内存溢出时，深度优先搜索不失为一种有效的算法。
5. 从输出结果可看出，深度优先搜索找到的第一个解并不一定是最优解。

如果要求出最优解的话，一种方法将是后面要介绍的动态规划法，另一种方法是修改原算法：把原输出过程的地方改为记录过程，即记录达到当前目标的路径和相应的路程值，并与前面已记录的值进行比较，保留其中最优的，等全部搜索完成后，才把保留的最优解输出。

3.2.广度优先搜索法的特点

1. 在产生新的子结点时，深度越小的结点越先得到扩展，即先产生它的子结点。为使算法便于实现，存放结点的数据库一般用队列的结构。
2. 无论问题性质如何不同，利用广度优先搜索法解题的基本算法是相同的，但数据库中每一结点内容，产生式规则，根据不同的问题，有不同的内容和结构，就是同一问题也可以有不同的表示方法。
3. 当结点到跟结点的费用（有的书称为耗散值）和结点的深度成正比时，特别是当每一结点到根结点的费用等于深度时，用广度优先法得到的解是最优解，但如果不成正比，则得到的解不一定是最优解。这一类问题要求出最优解，一种方法是使用后面要介绍的其他方法求解，另外一种方法是改进前面深度（或广度）优先搜索算法：找到一个目标后，不是立即退出，而是记录下目标结点的路径和费用，如果有多个目标结点，就加以比较，留下较优的结点。把所有可能的路径都搜索完后，才输出记录的最优路径。
4. 广度优先搜索算法，一般需要存储产生的所有结点，占的存储空间要比深度优先大得多，因此程序设计中，必须考虑溢出和节省内存空间得问题。
5. 比较深度优先和广度优先两种搜索法，广度优先搜索法一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索算法法要快些。

总之，一般情况下，深度优先搜索法占内存少但速度较慢，广度优先搜索算法占内存多但速度较快，在距离和深度成正比的情况下能较快地求出最优解。因此在选择用哪种算法时，要综合考虑。决定取舍。

3.3.优缺点比较

广搜优缺点

优点

• 对于解决最短或最少问题特别有效，而且寻找深度小
• 每个结点只访问一遍，结点总是以最短路径被访问，所以第二次路径确定不会比第一次短

缺点

• 内存耗费量大（需要开大量的数组单元用来存储状态）

使用场景：计算网络数据链路层的最短跳数，走迷宫的最短路径

深搜优缺点

优点

• 能找出所有解决方案
• 优先搜索一棵子树，然后是另一棵，所以和广搜对比，有着内存需要相对较少的优点

缺点

• 要多次遍历，搜索所有可能路径，标识做了之后还要取消。
• 在深度很大的情况下效率不高

Reference

https://blog.csdn.net/qq_41738049/article/details/94338715

https://blog.csdn.net/weixin_44341938/article/details/102250450