【deep_thoughts】45_BatchNorm、LayerNorm、InstanceNorm、GroupNorm原理及pytorch手写实现API
文章目录
- 1.Batch Normalization
- 2.Layer Normalization
- 3.Instance Normalization
- 4.Group Normalization
视频链接: 45、五种归一化的原理与PyTorch逐行手写实现讲解(BatchNorm/LayerNorm/InsNorm/GroupNorm/WeightNorm)_哔哩哔哩_bilibili
备注:视频中使用的是3维[N,L,C]作为例子,本文以CV中常用的4维[N,C,H,W]进行改写举例。

1.Batch Normalization
BatchNorm2d API:BatchNorm2d — PyTorch 1.13 documentation

eps:通常用于分母的数值稳定性。如果分母是0,再加上这样一个微小的量,可以保证除法能够正常进行。eps默认的是用的是1e-5,即0. 00001。
momentum:动量。moment 通常需要跟 track_running_state 联合起来理解。通常统计量是通过这种滑动平均来算出来的,不是单一时刻的 Mini-Batch ,它是一个累计的过程,从而提高估计准确度。
affine:公式中的 γ \gamma γ 和 β \beta β。当做完归一化之后,可以再给它加一个映射,将其映射到另外一个新的分布上。相当于做一个rescale和recenter。
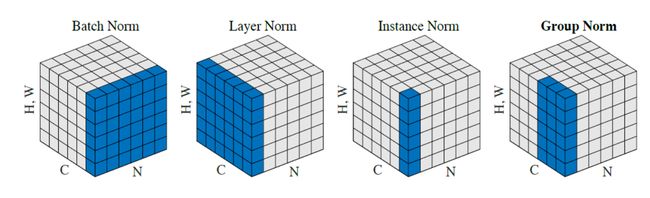
理解成:一个通道一个通道地进行归一化。
N = 4 # N:batch_size
C = 6 # C:features or channels
H, W = 2, 2
input = torch.randn(N, C, H, W)
# 1.实现 batch_norm 并验证 API
# per channel across mini-batch
# 1) 调用batch_norm API
batch_norm_op = nn.BatchNorm2d(C, affine=False) # affine 默认为真,此模块具有可学习的仿射参数
bn_y = batch_norm_op(input)
# BatchNorm2d的输入是(N,C,H,W)
# 2) 手写 batch_norm
bn_mean = input.mean(dim=(0, 2, 3), keepdim=True) # 对每一个通道求平均值,所以是除了通道的维度,计算平均值
bn_std = input.std(dim=(0, 2, 3), unbiased=False, keepdim=True) # 默认使用贝塞尔校正,把unbiased设置为False
verify_bn_y = (input - bn_mean)/(bn_std + 1e-5) # 加上防止分母消失的 1e-5
print(bn_y) # shape 均为 [4,6,2,2]
print(verify_bn_y) # 激动人心!!一毛一样!!
结果如下,可以看到结果一样,所以手写正确:
tensor([[[[ 0.3865, -1.2412],
[ 0.7278, 0.2328]],
[[ 0.4089, -2.0308],
[-0.3413, 1.0337]],
...
[[-0.3208, -1.9220],
[ 0.3307, 0.3614]]]])
tensor([[[[ 0.3865, -1.2412],
[ 0.7278, 0.2328]],
[[ 0.4089, -2.0308],
[-0.3413, 1.0337]],
...
[[-0.3208, -1.9220],
[ 0.3307, 0.3614]]]])
2.Layer Normalization
API: LayerNorm — PyTorch 1.13 documentation
官方文档中有对LayerNorm中关于NLP和CV两种维度形式进行举例。
理解成:一个batch一个batch地进行归一化。
# 2.实现 layer_norm 并验证 API
# per sample
# 1) 调用 layer_norm API
layer_norm_op = nn.LayerNorm([C, H, W], elementwise_affine=False) # 官网给了NLP和CV的两种写法
ln_y = layer_norm_op(input)
# 2) 手写 layer_norm
ln_mean = input.mean(dim=(1, 2, 3), keepdim=True) # 对每一个batch求平均值,所以是除了N的维度,计算平均值
ln_std = input.std(dim=(1, 2, 3), unbiased=False, keepdim=True)
verify_ln_y = (input - ln_mean)/(ln_std + 1e-5)
print(ln_y) # shape 均为 [4,6,2,2]
print(verify_ln_y) # 一毛一样
结果如下,可以看到结果一样,所以手写正确:
tensor([[[[ 1.0920, 0.8917],
[-1.5674, -1.0280]],
[[ 0.8238, -1.1087],
[-0.9046, -0.3045]],
...
[[ 0.5036, -1.3932],
[ 0.6199, 3.0223]]]])
tensor([[[[ 1.0920, 0.8917],
[-1.5674, -1.0280]],
[[ 0.8237, -1.1087],
[-0.9046, -0.3045]],
...
[[ 0.5036, -1.3932],
[ 0.6199, 3.0223]]]])
3.Instance Normalization
InstanceNorm2d API:InstanceNorm2d — PyTorch 1.13 documentation
理解成:对每个batch,每个channel进行归一化。
# 3.实现 instance_norm 并验证 API
# per sample, per channel
# 1) 调用 ins_norm API
ins_norm_op = nn.InstanceNorm2d(C, affine=False) # 传入通道维,默认 affine=False
in_y = ins_norm_op(input)
# 2) 手写 ins_norm
in_mean = input.mean(dim=(-1, -2), keepdim=True) # 除去样本维N和通道维C之外,剩下的H、W计算均值和标准差
in_std = input.std(dim=(-1, -2), unbiased=False, keepdim=True)
verify_in_y = (input - in_mean)/(in_std + 1e-5)
print(in_y) # shape 均为 [4,6,2,2]
print(verify_in_y) # 一毛一样!!
结果如下,可以看到结果一样,所以手写正确:
tensor([[[[-0.7156, -0.9186],
[ 0.0083, 1.6260]],
[[ 0.4793, -1.3396],
[ 1.3261, -0.4658]],
...
[[ 0.0386, -1.2782],
[-0.2736, 1.5132]]]])
tensor([[[[-0.7156, -0.9186],
[ 0.0083, 1.6260]],
[[ 0.4793, -1.3396],
[ 1.3261, -0.4658]],
...
[[ 0.0386, -1.2782],
[-0.2736, 1.5132]]]])
4.Group Normalization
API:GroupNorm — PyTorch 1.13 documentation
理解成:GroupNorm将通道划分成num_groups份,每一份为1个group,然后每个group进行与LayerNorm相同的操作,即一个batch一个batch地归一化。
# 4.实现 group_norm 并验证 API
# per sample, per group
# 1) 调用 group_norm API
num_groups = 2
group_norm_op = nn.GroupNorm(num_groups, num_channels=C, affine=False) # 传入groups数和通道维度,默认 affine=True
gn_y = group_norm_op(input)
# 2) 手写 group_norm
group_inputs = torch.split(input, split_size_or_sections=C // num_groups, dim=1) # 按照通道维进行切分
results = []
for g_input in group_inputs: # 相当于按照通道进行切分之后
gn_mean = g_input.mean(dim=(1, 2, 3), keepdim=True) # per group已经操作过了,现在是per sample,除了sample,其余维进行求均值和标准差
gn_std = g_input.std(dim=(1, 2, 3), unbiased=False, keepdim=True)
gn_result = (g_input - gn_mean)/(gn_std + 1e-5)
results.append(gn_result)
verify_gn_y = torch.cat(results, dim=1) # 按照通道维进行合并
print(gn_y) # shape 均为 [4,6,2,2]
print(verify_gn_y) # 一毛一样!!
结果如下,可以看到结果一样,所以手写正确:
tensor([[[[ 1.9588, 0.5271],
[-0.5983, -0.0513]],
[[ 0.3268, 0.1549],
[ 0.0202, -0.0592]],
...
[[-1.2460, 0.4658],
[-2.1641, 0.0483]]]])
tensor([[[[ 1.9587, 0.5271],
[-0.5983, -0.0513]],
[[ 0.3268, 0.1549],
[ 0.0202, -0.0592]],
...
[[-1.2460, 0.4658],
[-2.1641, 0.0483]]]])