机器学习笔记 - 时间序列的趋势分量
一、什么是趋势?
时间序列的趋势分量代表序列均值的持续、长期变化。 趋势是一系列中移动最慢的部分,代表了最大时间尺度的重要性。 在产品销售的时间序列中,随着越来越多的人知道该产品,市场扩张的影响可能是增加趋势。
在这里,我们将关注均值趋势。 更一般地说,一个序列中任何持续的和缓慢移动的变化都可能构成一个趋势——例如,时间序列通常在其变化中具有趋势。
二、移动平均线图
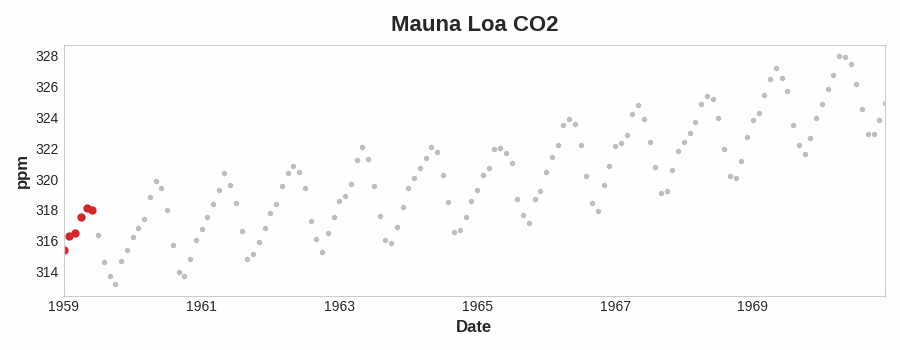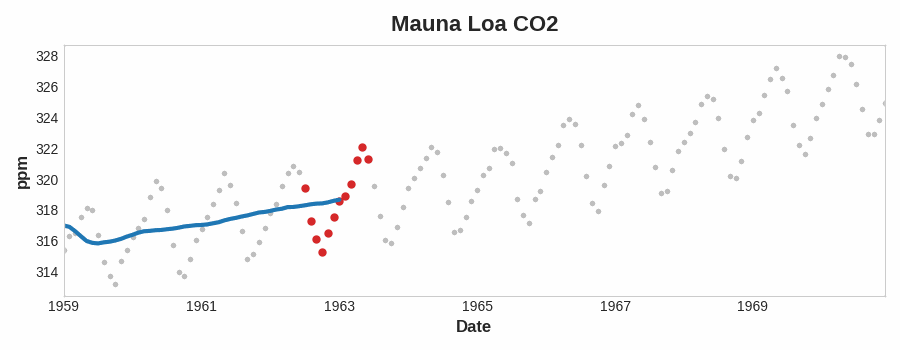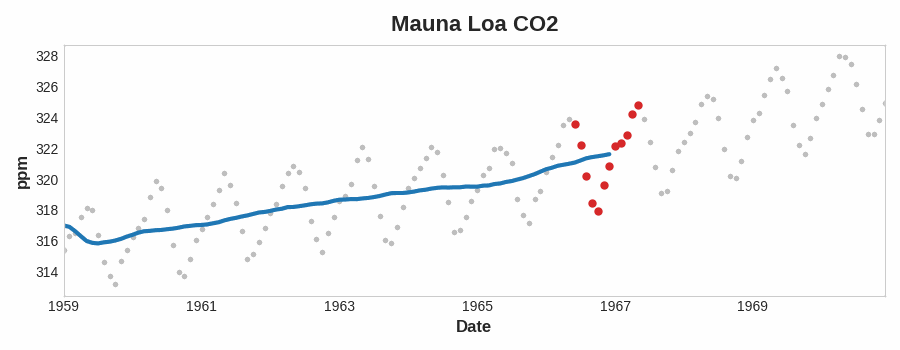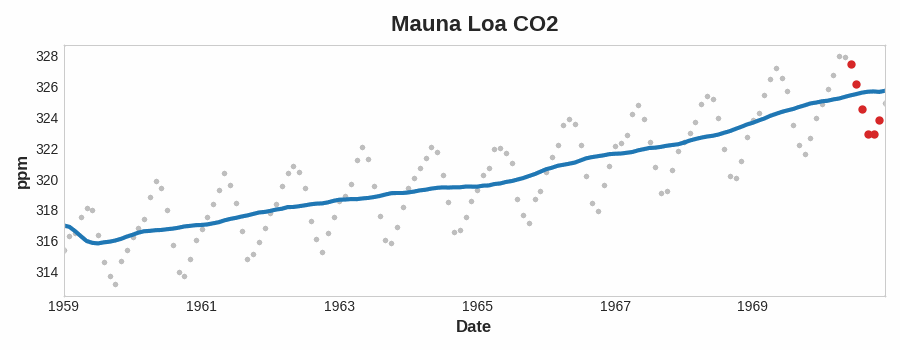
要查看时间序列可能具有什么样的趋势,我们可以使用移动平均图。 为了计算时间序列的移动平均值,我们计算某个定义宽度的滑动窗口内的值的平均值。 图表上的每个点代表位于任一侧窗口内的系列中所有值的平均值。 这个想法是为了消除序列中的任何短期波动,以便只保留长期变化。
注意上面的 Mauna Loa 系列是如何年复一年地重复上下运动的——一种短期的季节性变化。 要使变化成为趋势的一部分,它应该比任何季节性变化发生的时间更长。 因此,为了可视化趋势,我们在比该系列中的任何季节性周期更长的时间段内取平均值。 对于 Mauna Loa 系列,我们选择了一个大小为 12 的窗口来平滑每年的季节。
三、工程趋势
一旦我们确定了趋势的形状,我们就可以尝试使用时间步长特征对其进行建模。 我们已经看到如何使用时间虚拟模型本身来模拟线性趋势:
target = a * time + b我们可以通过时间虚拟变量的转换来拟合许多其他类型的趋势。 如果趋势看起来是二次的(抛物线),我们只需将时间虚拟变量的平方添加到特征集,得到:
target = a * time ** 2 + b * time + c线性回归将学习系数 a、b 和 c。
下图中的趋势曲线都是使用这些特征和 scikit-learn 的 LinearRegression 拟合的:
如果您以前没有见过这个技巧,那么您可能没有意识到线性回归可以拟合除直线以外的曲线。 这个想法是,如果您可以提供适当形状的曲线作为特征,那么线性回归可以学习如何以最适合目标的方式组合它们。
四、示例 - 隧道流量
在本例中,我们将为隧道交通数据集创建一个趋势模型。
from pathlib import Path
from warnings import simplefilter
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
simplefilter("ignore") # ignore warnings to clean up output cells
# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 5))
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=14,
titlepad=10,
)
plot_params = dict(
color="0.75",
style=".-",
markeredgecolor="0.25",
markerfacecolor="0.25",
legend=False,
)
%config InlineBackend.figure_format = 'retina'
# Load Tunnel Traffic dataset
data_dir = Path("../input/ts-course-data")
tunnel = pd.read_csv(data_dir / "tunnel.csv", parse_dates=["Day"])
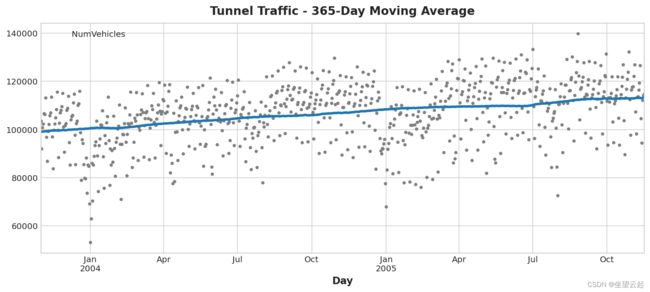
tunnel = tunnel.set_index("Day").to_period()让我们做一个移动平均线图,看看这个系列有什么样的趋势。 由于这个系列有每日观察,让我们选择一个 365 天的窗口来平滑一年内的任何短期变化。
要创建移动平均线,首先使用滚动方法开始窗口计算。 按照这个方法计算窗口的平均值。 正如我们所看到的,隧道流量的趋势似乎是线性的。
moving_average = tunnel.rolling(
window=365, # 365-day window
center=True, # puts the average at the center of the window
min_periods=183, # choose about half the window size
).mean() # compute the mean (could also do median, std, min, max, ...)
ax = tunnel.plot(style=".", color="0.5")
moving_average.plot(
ax=ax, linewidth=3, title="Tunnel Traffic - 365-Day Moving Average", legend=False,
);在上一个关于时间序列的文章中,我们直接在 Pandas 中设计了我们的时间虚拟机。 然而,从现在开始,我们将使用 statsmodels 库中的一个名为 DeterministicProcess 的函数。 使用这个函数将帮助我们避免一些棘手的失败案例,这些案例可能会随着时间序列和线性回归而出现。 order 参数是指多项式顺序:1 表示线性,2 表示二次,3 表示三次,依此类推。
from statsmodels.tsa.deterministic import DeterministicProcess
dp = DeterministicProcess(
index=tunnel.index, # dates from the training data
constant=True, # dummy feature for the bias (y_intercept)
order=1, # the time dummy (trend)
drop=True, # drop terms if necessary to avoid collinearity
)
# `in_sample` creates features for the dates given in the `index` argument
X = dp.in_sample()
X.head()| Day | const | trend |
|---|---|---|
| 2003-11-01 | 1.0 | 1.0 |
| 2003-11-02 | 1.0 | 2.0 |
| 2003-11-03 | 1.0 | 3.0 |
| 2003-11-04 | 1.0 | 4.0 |
| 2003-11-05 | 1.0 | 5.0 |
(顺便说一下,确定性过程是非随机或完全确定的时间序列的技术术语,就像 const 和趋势序列一样。从时间指数派生的特征通常是确定性的。)
我们基本上像以前一样创建趋势模型,但请注意添加了 fit_intercept=False 参数。
from sklearn.linear_model import LinearRegression
y = tunnel["NumVehicles"] # the target
# The intercept is the same as the `const` feature from
# DeterministicProcess. LinearRegression behaves badly with duplicated
# features, so we need to be sure to exclude it here.
model = LinearRegression(fit_intercept=False)
model.fit(X, y)
y_pred = pd.Series(model.predict(X), index=X.index)我们的线性回归模型发现的趋势几乎与移动平均图相同,这表明在这种情况下线性趋势是正确的决定。
ax = tunnel.plot(style=".", color="0.5", title="Tunnel Traffic - Linear Trend")
_ = y_pred.plot(ax=ax, linewidth=3, label="Trend")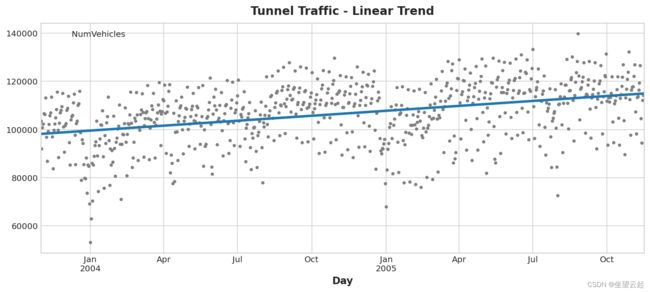 为了进行预测,我们将模型应用于“样本外”特征。 “样本外”是指训练数据的观察期之外的时间。 以下是我们如何进行 30 天预测的方法:
为了进行预测,我们将模型应用于“样本外”特征。 “样本外”是指训练数据的观察期之外的时间。 以下是我们如何进行 30 天预测的方法:
X = dp.out_of_sample(steps=30)
y_fore = pd.Series(model.predict(X), index=X.index)
y_fore.head()2005-11-17 114981.801146 2005-11-18 115004.298595 2005-11-19 115026.796045 2005-11-20 115049.293494 2005-11-21 115071.790944 Freq: D, dtype: float64
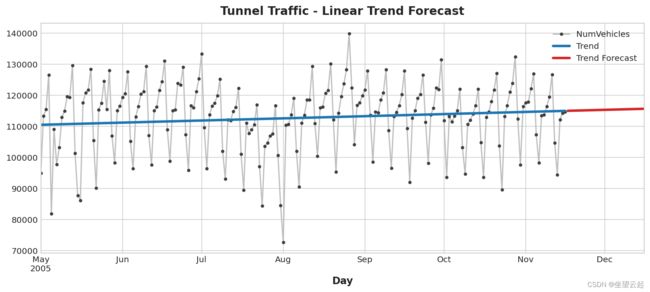
让我们绘制该系列的一部分以查看未来 30 天的趋势预测:
ax = tunnel["2005-05":].plot(title="Tunnel Traffic - Linear Trend Forecast", **plot_params)
ax = y_pred["2005-05":].plot(ax=ax, linewidth=3, label="Trend")
ax = y_fore.plot(ax=ax, linewidth=3, label="Trend Forecast", color="C3")
_ = ax.legend()趋势模型之所以有用,有很多原因。 除了作为更复杂模型的基线或起点之外,我们还可以将它们用作“混合模型”中的一个组件,其中算法无法学习趋势(如 XGBoost 和随机森林)。