CV任务中如何解决图像光照度不均匀的问题

01.图像光照对于图像任务的影响

在以图像视觉为主的CV任务当中，经常会遇到图像光照不均匀的情况，这种情况往往会影响到图像的对比度问题，从而影响到CV任务的最终结果。比如我们在做人脸识别的时候，由于每个人所处的环境的不同，目标人物脸上的光照情况也是不一样的，我们无法保证每个人的人脸光照度都是均匀的。那么就有可能会影响到最终识别的结果。如果出现这种情况，是需要我们进行一定的处理的。

一般来说，如果人脸的光照度不均匀，往往会出现可识别特征减少的情况。比如人脸光照度过高会导致被识别目标区域曝光，反应到图像上就是像素值整体偏大，甚至于接近最大值255（纯白色）；反之，如果光照度过低则会导致被识别目标区域失光，反应到图像上就是像素值整体偏低，甚至于接近最小值0（纯黑色）。

无论是光照度过高还是过低，都不适合我们对于特征的提取（点击了解：深度学习之神经网络特征综述），目标识别任务对于数据的要求是极高的，连人工智能权威学者吴恩达都说人工智能=80%数据+20%算法，可见数据对于人工智能最终呈现出的效果有多大的影响。而数据本身对于人工智能模型输出结果的影响体现就是数据的质量，户外或者室内的光照度的不同对于数据的影响是保证数据质量的极大挑战之一。

---

02.图像光照问题的解决方法

对于图像数据受到光照度不足或者曝光引起的对比度太小的情况，在图像处理中一般是图像直方图均衡化的方法来处理。直方图均衡化是通过拉伸像素强度分布范围来增强图像对比度的一种方法。例如，更亮的图像将所有像素限制在高值。但是一个好的图像会有来自图像所有区域的像素。因此，我们需要将这个直方图扩展到两端，而这就是直方图均衡化所做的事情(用简单的话来说)。这通常会改善图像的对比度。

因为直方图均衡化处理之后，原来比较少像素的灰度会被分配到别的灰度去，像素相对集中， 处理后灰度范围变大，对比度变大，清晰度变大，所以能有效增强图像。直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。这种方法通常用来增加许多图像的局部对比度，尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法，亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能。

直方图均衡化的基本原理是：对在图像中像素个数多的灰度值（即对画面起主要作用的灰度值）进行展宽，而对像素个数少的灰度值（即对画面不起主要作用的灰度值）进行归并，从而增大对比度，使图像清晰，达到增强的目的。

要想实现图像直方图均衡化的效果, 对于原图像的直方图需要做一个分布函数的映射，这个映射函数就是累积分布函数。我们在开始之前还需要考虑两个问题：第一个我问题是为什么要选用累积分布函数，第二个问题是为什么使用累积分布函数处理后像素值会均匀分布。

首先来看看第一个问题：在均衡化过程中，必须要保证两个条件：

①像素无论怎么映射，一定要保证原来的大小关系不变，较亮的区域，依旧是较亮的，较暗依旧暗，只是对比度增大，绝对不能明暗颠倒；

②如果是八位图像，那么像素映射函数的值域应在0和255之间的，不能越界。

综合以上两个条件，累积分布函数是个好的选择，因为累积分布函数是单调增函数（控制大小关系），并且值域是0到1（控制越界问题），所以直方图均衡化中使用的是累积分布函数。

再来看看第二个问题：累积分布函数具有一些比较好的性质，比较一下概率分布函数和累积分布函数，不难发现前者的二维图像是参差不齐的，而后者的图像是单调递增的。在直方图均衡化过程中，映射方法是:

其中，n是图像中像素的总和，是当前灰度级的像素个数，L是图像中可能的灰度级总数。

---

03.解决图像光照问题的代码实现

 

一般来说光照度对于图像的影响可以分为两种：整体影响和局部影响。

整体影响是指图像整体的光照度偏亮或者偏暗，这种情况相对来说比较容易处理，最简单的办法就是对全图做一次均衡化处理。

在OpenCv中，有专门针对图像光照度问题的图像直方图均衡化处理方法，就是用来处理图像光照度过亮或者过暗的问题的。

首先我们需要对图像进行一次灰度值的统计，然后将统计出来的直方图进行拉伸，从而达到均衡化的目的。下面我们将会针对一张光照度不足的图像进行全图的直方图均衡化，然后将均衡化前后的结果做一个对比，方便大家更直观的了解图像直方图均衡化的效果。

使用opencv对图像进行全局直方图均衡化处理的实现代码：

# 1）全局直方图均衡化# src = cv2.imread("../images/28.jpg",0)src = cv2.imread("./images/1.jpg",0)​# 全局直方图均衡化dst = cv2.equalizeHist(src)​# 原直方图hist_src = cv2.calcHist([src], [0], None, [256], [0, 255])# 全局均衡化后的直方图hist_dst = cv2.calcHist([dst], [0], None, [256], [0, 255])​# # 结合matplotlib展示多张图片plt.subplot(211), plt.imshow(src, cmap="gray"), plt.title("Src Image")plt.xticks([]), plt.yticks([])plt.subplot(212), plt.imshow(dst, cmap="gray"), plt.title("Dst Image")plt.xticks([]), plt.yticks([])plt.show()plt.subplot(211), plt.plot(hist_src, color="r", label="hist_src"), plt.legend()plt.subplot(212), plt.plot(hist_dst, color="b", label="hist_dst"), plt.legend()plt.show()

下面是全局直方图均衡化前后的图像对比效果：

可以发现,，无论是风景照还是人像照片，均衡化前后的图像对比都是非常明显的，原图有一种类似雾气或者黑影笼罩的感觉，通过直方图均衡化处理之后，图像的对比度和亮度明显增加了不少。

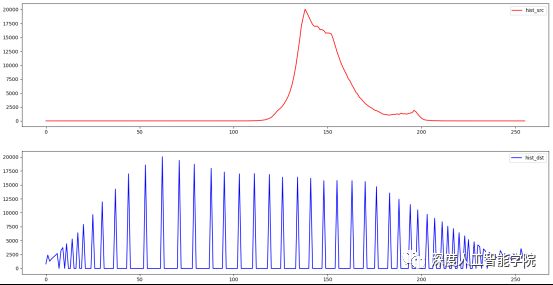
再来看看全局直方图均衡化前后的直方图变化情况：

以上是对两张不同的图像做全图直方图均衡化后的直方图展示，这种图像直方图的均衡化方法也称为全局直方图均衡化方法，主要是解决前面说到的光照度对于图像整体影响的问题。可以发现均衡化前后的直方图的形状会被拉伸，图像均衡化方法会将图像中灰度值出现频率较高的部分的分布拉伸扩展到了全图，从而增加了图像的亮度和对比度。

以上这种对于图像进行全局直方图均衡化的方法并不是适合所有场景下的图像均衡化，我们能够发现上面的直方图均衡化统计的是全图的灰度像素值，从而进行对高频部分扩展来达到均衡化的目的，但是现实情况是不一定所有的图像都是均匀的光照度较低或者灰暗，而是有的部分光照较多，有的部分光照较少。像这种情况就不适合对图像做全局的均衡化，因为这样做会让全图整体变亮，虽然会使得图像较暗的部分变亮，但也会让原本就亮的部分变得更亮，很有可能会曝光。

所以最好的办法就是对图像进行分而治之，简单来说，就是在图像上画格子，把一幅图像分割成若干个n*n的格子，然后在每个格子内做均衡化，由于图像是属于局部像素变化比较大的情况，使用自适应的局部直方图均衡化就不会影响到全图了。

值得注意的是在做直方图均衡化之前要根据图像的具体情况选定格子的大小，不然格子过大或者过小都有可能会影响到图像均衡化的结果。

使用opencv对图像进行自适应局部直方图均衡化处理的实现代码：

# 2）CLAHE(限制对比度的自适应直方图均衡化)# src = cv2.imread("../images/29.jpg", cv2.IMREAD_GRAYSCALE)​src = cv2.imread("./images/2.jpg", cv2.IMREAD_GRAYSCALE)​# 1.全局直方图均衡化img_equalize = cv2.equalizeHist(src)​​# 2.CLAHE自适应均衡化# createCLAHE(clipLimit=None, tileGridSize=None)clahe = cv2.createCLAHE(tileGridSize=(5,5))img_clahe = clahe.apply(src)​# 原直方图hist_src = cv2.calcHist([src], [0], None, [256], [0, 255])# 全局均衡化后的直方图hist_equalize = cv2.calcHist([img_equalize], [0], None, [256], [0, 255])# CLAHE均衡化后的直方图hist_clahe = cv2.calcHist([img_clahe], [0], None, [256], [0, 255])​# 结合matplotlib展示多张图片plt.subplot(311), plt.imshow(src, cmap="gray"), plt.title("Src Image")plt.xticks([]), plt.yticks([])plt.subplot(312), plt.imshow(img_equalize, cmap="gray"), plt.title("Image after Equalzie")plt.xticks([]), plt.yticks([])plt.subplot(313), plt.imshow(img_clahe, cmap="gray"), plt.title("Image after CLAHE")plt.xticks([]), plt.yticks([])plt.show()plt.subplot(311), plt.plot(hist_src, color="b", label="hist_src"), plt.legend()plt.subplot(312), plt.plot(hist_equalize, color="g", label="hist_equalize"), plt.legend()plt.subplot(313), plt.plot(hist_clahe, color="r", label="hist_clahe"), plt.legend()plt.show()

下面是对图像进行全局直方图均衡化和自适应局部直方图均衡化前后的对比效果：

通过上面两张图像的展示效果，我们发现直接对局部较暗或者较亮的图像进行全局直方图均衡化，会导致较亮的图像部分曝光，而较暗的图像部分也有可能没有达到预期的效果。

而使用了自适应的局部直方图均衡化方法不但会使得图像原本较暗的部分变亮之外，较亮的部分也不会发生曝光的现象。

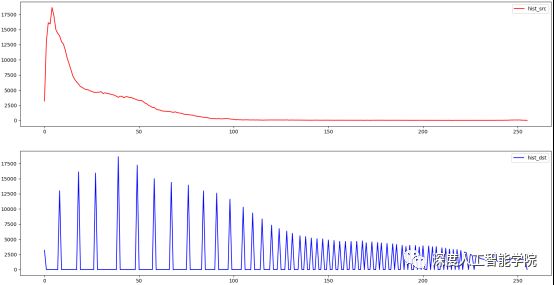
同样我们也可以观察一下原图像的直方图，以及全局直方图和自适应的局部直方图的区别：

从以上两张图像的局部直方图均衡化结果上可以很明显的看出，直接对图像做全局直方图均衡化，是对原直方图的高频部分等比例拉伸，而自适应的局部直方图均衡化方法会对低频部分的拉伸更多，从而使得局部信息变化更大，达到局部均衡化的效果。

图像直方图均衡化作为图像亮度和对比度的处理方法，在图像检测识别领域应用中能够有效地提高检测率和识别率，但是最根本的方法还是要从数据采集端把控质量才是最根本的解决办法。

深度人工智能学院是成都深度智谷科技旗下的教育品牌，我们会为人工智能学习者呈现最实用的干货技能，也会为人工智能从业者考取人工智能相关的证书提供报考服务，有意者可以联系我们。

中国人工智能学会部分证书样本：

​

工信部人工智能证书样本：

文中所使用的部分图片来自网络素材，如果有侵权，请第一时间联系我们删除！

---

 关注微信公众号：深度人工智能学院，获取更多人工智能方面的知识！