【蓝桥杯算法练习题】递归与递推

一、AcWing 92. 递归实现指数型枚举

【题目描述】
从$1\sim n$这$n$个整数中随机选取任意多个，输出所有可能的选择方案。

【输入格式】
输入一个整数$n$。

【输出格式】
每行输出一种方案。
同一行内的数必须升序排列，相邻两个数用恰好$1$个空格隔开。
对于没有选任何数的方案，输出空行。
本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

【数据范围】
$1\le n\le 15$

【输入样例】

3

【输出样例】

3
2
2 3
1
1 3
1 2
1 2 3

【分析】

---

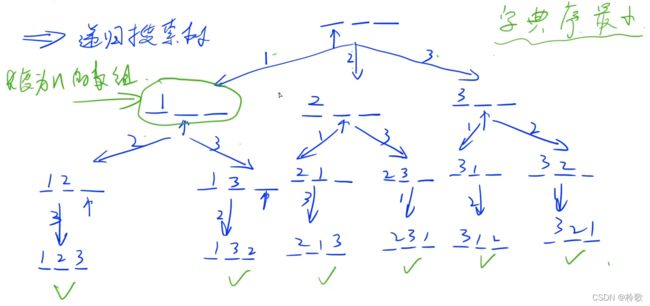
从$1\sim n$依次考虑每个数选还是不选，递归搜索树如下图所示：

---

【DFS写法代码】

#include 
using namespace std;

const int N = 20;
int n, st[N];//st[i]为0表示不选i,为1表示选i

void dfs(int u)
{
    if (u > n)
    {
        for (int i = 1; i <= n; i++)
            if (st[i]) cout << i << ' ';
        cout << endl;
        return;
    }
    for (int i = 0; i <= 1; i++)
        st[u] = i, dfs(u + 1);
}

int main()
{
    cin >> n;
    dfs(1);
    return 0;
}

【状态压缩写法代码】

#include 
using namespace std;

const int N = 20;
int n;

int main()
{
    cin >> n;
    for (int state = 0; state < 1 << n; state++)//state二进制表示中的第k位表示是否选第k个数
    {
        for (int i = 0; i < n; i++)
            if (state >> i & 1) cout << i + 1 << ' ';
        cout << endl;
    }
    return 0;
}

二、AcWing 94. 递归实现排列型枚举

【题目描述】
把$1\sim n$这$n$个整数排成一行后随机打乱顺序，输出所有可能的次序。

【输入格式】
一个整数$n$。

【输出格式】
按照从小到大的顺序输出所有方案，每行$1$个。
首先，同一行相邻两个数用一个空格隔开。
其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面。

【数据范围】
$1\le n\le 9$

【输入样例】

3

【输出样例】

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

【分析】

---

依次枚举每个位置放置哪个数即可，递归搜索树如下图所示：

---

【朴素写法代码】

#include 
using namespace std;

const int N = 10;
int res[N], st[N];//res保存排列结果,st表示1~n这几个数是否已被使用
int n;

void dfs(int u)
{
    if (u == n)
    {
        for (int i = 0; i < n; i++) cout << res[i] << ' ';
        cout << endl;
        return;
    }
    for (int i = 1; i <= n; i++)
        if (!st[i]) res[u] = i, st[i] = true, dfs(u + 1), st[i] = false;
}

int main()
{
    cin >> n;
    dfs(0);
    return 0;
}

【状态压缩写法代码】

#include 
using namespace std;

const int N = 10;
int res[N];//res保存排列结果
int n;

void dfs(int u, int state)//state的第i位如果为1表示i已被使用,为0表示未被使用
{
    if (u == n)
    {
        for (int i = 0; i < n; i++) cout << res[i] << ' ';
        cout << endl;
        return;
    }
    for (int i = 1; i <= n; i++)
        if (!(state >> i & 1)) res[u] = i, dfs(u + 1, state | 1 << i);
}

int main()
{
    cin >> n;
    dfs(0, 0);
    return 0;
}

三、AcWing 717. 简单斐波那契

【题目描述】
以下数列0 1 1 2 3 5 8 13 21 ...被称为斐波纳契数列。
这个数列从第$3$项开始，每一项都等于前两项之和。
输入一个整数$N$，请你输出这个序列的前$N$项。

【输入格式】
一个整数$N$。

【输出格式】
在一行中输出斐波那契数列的前$N$项，数字之间用空格隔开。

【数据范围】
$0<N<46$

【输入样例】

5

【输出样例】

0 1 1 2 3

【分析】

---

递推水题，无需分析。

---

【代码】

#include 
using namespace std;

const int N = 50;
int n, f[N];

int main()
{
    cin >> n;
    f[1] = 1;
    for (int i = 2; i < n; i++) f[i] = f[i - 2] + f[i - 1];
    for (int i = 0; i < n; i++) cout << f[i] << ' ';
    return 0;
}

四、AcWing 95. 费解的开关

【题目描述】
你玩过“拉灯”游戏吗？
$25$盏灯排成一个$5\times 5$的方形。
每一个灯都有一个开关，游戏者可以改变它的状态。
每一步，游戏者可以改变某一个灯的状态。
游戏者改变一个灯的状态会产生连锁反应：和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字$1$表示一盏开着的灯，用数字$0$表示关着的灯。

例如下面这种状态：

10111
01101
10111
10000
11011

在改变了最左上角的灯的状态后将变成：

01111
11101
10111
10000
11011

再改变它正中间的灯后状态将变成：

01111
11001
11001
10100
11011

给定一些游戏的初始状态，编写程序判断游戏者是否可能在$6$步以内使所有的灯都变亮。

【输入格式】
第一行输入正整数$n$，代表数据中共有$n$个待解决的游戏初始状态。
以下若干行数据分为$n$组，每组数据有$5$行，每行$5$个字符。
每组数据描述了一个游戏的初始状态。
各组数据间用一个空行分隔。

【输出格式】
一共输出$n$行数据，每行有一个小于等于$6$的整数，它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态，若$6$步以内无法使所有灯变亮，则输出$-1$。

【数据范围】
$0<n\le 500$

【输入样例】

3
00111
01011
10001
11010
11100

11101
11101
11110
11111
11111

01111
11111
11111
11111
11111

【输出样例】

3
2
-1

【分析】

---

本题有两种解题思路：

1. 使用BFS将终点状态（全为$1$）反推$6$步所能到达的所有状态搜索出来，然后根据每次输入的状态直接查表判断是否合法即可。
2. 枚举第一行所有开关的全部可能的状态，可以使用一个二进制数$state$，它的第$i$位表示第$i$个开关是否按下。当第一行的状态确定了，我们从第二行开始逐行枚举每一个开关，如果当前开关$(i,j)$的上一个开关状态是0，即$g[i-1][j]={=}^{\prime }{0}^{\prime }$，那么当前开关一定要按，因为是逐行枚举的，上一行的状态已经是确定的了，也就是无法再按了，只有当前开关能改变上一行开关的状态。那么我们枚举完后面四行时，第$1\sim 4$行一定已经全为1了，这时候我们枚举最后一行的每个开关，如果每个开关的状态都为1，那么用记录下的操作次数去更新最终答案。最后判断最终答案是否小于$6$即可。

方法一的时间复杂度难以计算，因此选用第二种方法。
PS：字符0（ASCII码为$48$）与字符1（ASCII码为$49$）相互转换的方式为^=1即可，因为二进制表示中只有最后一位不同。

---

【代码】

#include 
#include 
#include 
using namespace std;

const int N = 10;
char g[N][N], backup[N][N];
int n;
int dx[5] = { -1, 0, 1, 0, 0 }, dy[5] = { 0, 1, 0, -1, 0 };

void op(int x, int y)
{
    for (int i = 0; i < 5; i++)
    {
        int nx = x + dx[i], ny = y + dy[i];
        if (nx >= 0 && nx < 5 && ny >= 0 && ny < 5) g[nx][ny] ^= 1;
    }
}

int main()
{
    cin >> n;
    while (n--)
    {
        for (int i = 0; i < 5; i++) cin >> backup[i];
        int res = N;
        for (int state = 0; state < 32; state++)
        {
            memcpy(g, backup, sizeof backup);
            int cnt = 0;
            for (int i = 0; i < 5; i++)
                if (state >> i & 1) op(0, i), cnt++;
            for (int i = 1; i < 5; i++)
                for (int j = 0; j < 5; j++)
                    if (g[i - 1][j] == '0') op(i, j), cnt++;
            for (int i = 0; i < 5; i++)
                if (g[4][i] == '0') break;
                else if (i == 4) res = min(res, cnt);
        }
        if (res > 6) cout << -1 << endl;
        else cout << res << endl;
    }
    return 0;
}

五、AcWing 93. 递归实现组合型枚举

【题目描述】
从$1\sim n$这$n$个整数中随机选出$m$个，输出所有可能的选择方案。

【输入格式】
两个整数$n,m$，在同一行用空格隔开。

【输出格式】
按照从小到大的顺序输出所有方案，每行$1$个。
首先，同一行内的数升序排列，相邻两个数用一个空格隔开。
其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面（例如1 3 5 7排在1 3 6 8前面）。

【数据范围】
$n>0$
$0\le m\le n$
$n+(n-m)\le 25$

【输入样例】

5 3

【输出样例】

1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5

【分析】

---

组合型枚举与全排列不同的地方在于DFS时需要额外传入一个参数$start$，表示这个位置的数需要从$start$开始往后选，而不能选前面的数，其递归搜索树如下图所示：

优化：如果从$start$开始之后的所有数的数量小于当前剩余的空位则一定无解，直接剪枝即可。

---

【代码】

#include 
using namespace std;

const int N = 30;
int res[N];
int n, m;

void dfs(int u, int start)//当前位置为u,从start开始枚举每一个数
{
    if (n - start + 1 < m - u) return;//剪枝
    if (u == m)
    {
        for (int i = 0; i < m; i++) cout << res[i] << ' ';
        cout << endl;
        return;
    }
    for (int i = start; i <= n; i++) res[u] = i, dfs(u + 1, i + 1);
}

int main()
{
    cin >> n >> m;
    dfs(0, 1);
    return 0;
}

六、AcWing 1209. 带分数

【题目描述】
$100$可以表示为带分数的形式：$100=3+\frac{69258}{714}$
还可以表示为：$100=82+\frac{3546}{197}$
注意特征：带分数中，数字$1\sim 9$分别出现且只出现一次（不包含$0$）。
类似这样的带分数，$100$有$11$种表示法。

【输入格式】
一个正整数。

【输出格式】
输出输入数字用数码$1\sim 9$不重复不遗漏地组成带分数表示的全部种数。

【数据范围】
$1\le N<10^6$

【输入样例1】

100

【输出样例1】

11

【输入样例2】

105

【输出样例2】

6

【分析】

---

首先将带分数的形式表示成$n=a+\frac{b}{c}$，即$b=n\ast c-a\ast c$，因此我们可以枚举$a,c$，通过这两个值即可算出$b$的值。

首先开一个判重数组$st[i]$表示数字$i$是否已经用过，然后实现一个$dfs\_a$函数，函数有两个参数$u,a$，分别表示当前已经用了多少个数字以及$a$的值，由于$a,b,c$一定都要存在，因此都必须大于$0$。当$a>=n$时，一定无解，可以进行剪枝。否则$a$暂时就是合法的，进而可以枚举$c$（详细过程后文再说）。枚举$a$的方式也就是使用不同的数进行排列，可以通过将不同的数插入到$a$的末尾即可，例如：$1,12,123,13,132,2,21,213,\dots$

枚举$c$时我们也写一个$dfs\_c$函数，函数有三个参数$u,a,c$，前两个参数同$dfs\_a$一样，参数$c$表示$c$的值。如果当前的$c$合法（也就是不为$0$），那么我们就可以通过式子计算出$b$的值（需要注意$n\ast c$有可能爆$int$）。此时我们首先要判断$b$是否为$0$，如果为$0$则不合法；其次判断$b$中的每一位的数字是否为$0$或者已经在$a,c$中使用过，若是则不合法，若不是则将这个数字进行标记已使用；最后判断$1\sim 9$中的每一个数字是否都被使用了，如果有一个没被使用则不合法，否则$a,b,c$就是一组合法的解，答案加一。

---

【代码】

#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int N = 10;
bool st[N], temp[N];
int n, res;

bool check(int a, int c)
{
    LL b = (LL)n * c - a * c;//注意n*c可能会爆int
    if (!b) return false;
    memcpy(temp, st, sizeof st);//注意进行备份,因为要修改标记数组
    while (b)
    {
        int x = b % 10;//取b的个位数
        b /= 10;//把b的个位数删去
        if (!x || temp[x]) return false;//如果这一位为0或者重复出现则返回false
        temp[x] = true;
    }
    for (int i = 1; i <= 9; i++)//判断abc中的数字是否1~9全部出现过
        if (!temp[i]) return false;
    return true;
}

void dfs_c(int u, int a, int c)
{
    if (u > 9) return;//a和c的位数已经超过9位时肯定无解
    if (c > 0 && check(a, c)) res++;//当c>0时判断当前的ac取值是否合法
    for (int i = 1; i <= 9; i++)
        if (!st[i]) st[i] = true, dfs_c(u + 1, a, c * 10 + i), st[i] = false;
}

//u表示a和c的总位数
void dfs_a(int u, int a)
{
    if (a >= n) return;
    if (a > 0) dfs_c(u, a, 0);//当a>0时,枚举c的排列
    for (int i = 1; i <= 9; i++)//判断1~9是否使用过,如果没有那么在a的末尾插入这个数
        if (!st[i]) st[i] = true, dfs_a(u + 1, a * 10 + i), st[i] = false;
}

int main()
{
    cin >> n;
    dfs_a(0, 0);
    cout << res << endl;
    return 0;
}

七、AcWing 116. 飞行员兄弟

【题目描述】
“飞行员兄弟”这个游戏，需要玩家顺利的打开一个拥有$16$个把手的冰箱。
已知每个把手可以处于以下两种状态之一：打开或关闭。
只有当所有把手都打开时，冰箱才会打开。
把手可以表示为一个$4\times 4$的矩阵，您可以改变任何一个位置$[i,j]$上把手的状态。
但是，这也会使得第$i$行和第$j$列上的所有把手的状态也随着改变。
请你求出打开冰箱所需的切换把手的次数最小值是多少。

【输入格式】
输入一共包含四行，每行包含四个把手的初始状态。
符号+表示把手处于闭合状态，而符号-表示把手处于打开状态。
至少一个手柄的初始状态是关闭的。

【输出格式】
第一行输出一个整数$N$，表示所需的最小切换把手次数。
接下来$N$行描述切换顺序，每行输出两个整数，代表被切换状态的把手的行号和列号，数字之间用空格隔开。
注意：如果存在多种打开冰箱的方式，则按照优先级整体从上到下，同行从左到右打开。

【数据范围】
$1\le i,j\le 4$

【输入样例】

-+--
----
----
-+--

【输出样例】

6
1 1
1 3
1 4
4 1
4 3
4 4

【分析】

---

本题我们可以直接枚举每个位置的把手是开还是不开，总共有$2^{16}$种状态，可以使用状态压缩的方式表示状态。对于每一种确定的状态，我们将原数组操作一遍（操作的过程记下开把手的位置），得到操作后的数组，判断操作后是否每个位置都为-，如果都为-且开把手的次数小于最优解的次数，那么就更新最优解，由于我们是从小到大枚举状态的，因此最少次数的解一定也是字典序最小的操作方案。

---

【代码】

#include 
#include 
#include 
#include 
using namespace std;

typedef pair<int, int> PII;
const int N = 5;
char g[N][N], backup[N][N];
vector<PII> res;

void op(int x, int y)
{
    for (int i = 0; i < 4; i++)//操作(x,y)所在的行
        if (g[x][i] == '+') g[x][i] = '-';
        else g[x][i] = '+';
    for (int i = 0; i < 4; i++)//操作(x,y)所在的列
        if (i != x)//之前已经操作过点(x,y),因此不能重复操作
            if (g[i][y] == '+') g[i][y] = '-';
            else g[i][y] = '+';
}

int main()
{
    for (int i = 0; i < 4; i++) cin >> backup[i];
    for (int st = 0; st < 1 << 16; st++)//st的每一位表示这个开关按还是不按
    {
        memcpy(g, backup, sizeof backup);
        vector<PII> temp;
        for (int i = 0; i < 4; i++)
            for (int j = 0; j < 4; j++)
                if (st >> (i * 4 + j) & 1) op(i, j), temp.push_back({ i, j });
        for (int i = 0; i < 16; i++)//遍历一遍操作完的数组判断是否全为'-'
            if (g[i / 4][i % 4] == '+') break;
            else if (i == 15 && (res.empty() || temp.size() < res.size())) res = temp;
    }
    cout << res.size() << endl;
    for (auto t : res) cout << t.first + 1 << ' ' << t.second + 1 << endl;
    return 0;
}

八、AcWing 1208. 翻硬币

【题目描述】
小明正在玩一个“翻硬币”的游戏。
桌上放着排成一排的若干硬币。我们用*表示正面，用o表示反面（是小写字母，不是零）。
比如，可能情形是：**oo***oooo
如果同时翻转左边的两个硬币，则变为：oooo***oooo
现在小明的问题是：如果已知了初始状态和要达到的目标状态，每次只能同时翻转相邻的两个硬币，那么对特定的局面，最少要翻动多少次呢？
我们约定：把翻动相邻的两个硬币叫做一步操作。

【输入格式】
两行等长的字符串，分别表示初始状态和要达到的目标状态。

【输出格式】
一个整数，表示最小操作步数

【数据范围】
输入字符串的长度均不超过$100$。
数据保证答案一定有解。

【输入样例1】

**********
o****o****

【输出样例1】

5

【输入样例2】

*o**o***o***
*o***o**o***

【输出样例2】

1

【分析】

---

如果第一枚硬币不一样，那么一定得同时翻动第一和第二枚硬币。如果第二枚硬币不一样，那么一定得同时翻动第二枚和第三枚硬币，因为第一枚硬币已经匹配了。然后继续看第三枚以此类推，由于一定有解，因此到最后一枚硬币的时候一定是一样的。

---

【代码】

#include 
using namespace std;

const int N = 110;
char st[N], ed[N];
int res;

void op(int x)
{
    if (st[x] == '*') st[x] = 'o';
    else st[x] = '*';
}

int main()
{
    cin >> st >> ed;
    for (int i = 0; st[i]; i++)
        if (st[i] != ed[i]) op(i), op(i + 1), res++;
    cout << res << endl;
    return 0;
}