Day1递归与递推--蓝桥杯学习笔记

目录

递推与递归的简单应用

例题：递归实现指数型枚举

例题：递归实现排列型枚举 

Day1练习题

蓝桥杯2013年第四届真题--带分数 

蓝桥杯往届试题：翻硬币

车厢重组（冒泡排序）

蓝桥杯2014年第五届真题：波动数列

母牛的故事

明明的随机数

---

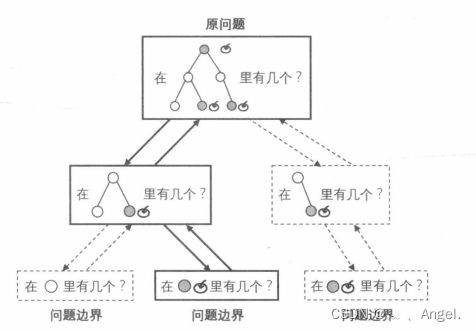
递推：以已知的“问题边界”为起点向“原问题”正向推导的扩展方式就是递推。

递归：然而在很多时候，推导的路线难以确定，这时以“原问题”为起点尝试寻找把状态空间缩小到已知的“问题边界”的路线，再通过该路线反向回溯的遍历方式就是递归。

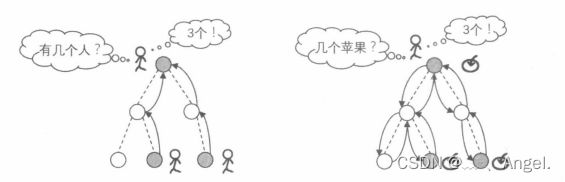
自身调用自身、回溯时还原现场，如下图所示：

下面两幅图来表示递推与递归的差别：

递推与递归的简单应用

在使用枚举算法蛮力探索问题的整个“状态空间”时，经常需要递归。按照规模大小，有如下几种常见的美剧形式和遍历方式：

例题：递归实现指数型枚举

 等价于每个整数可以选或者不选，所有可能的方案总数共有种

#include
int n,num,ans[10000];
void dfs(int dep){
	if(dep>n){
		for(int i=1;i<=num;i++){
			printf("%d ",ans[i]);
		}
		printf("\n");
		return;
	}
	//选
	ans[++num]=dep;
	dfs(dep+1);  //dep表示当前考虑的那个数
	//不选
	num--;
	dfs(dep+1);
}
int main(void){
	scanf("%d",&n);
	dfs(1);
	return 0;
}

#include
#include
using namespace std;
int n;
vector v; //动态长度数组（int型）
void dfs(int dep){
	if(dep>n){
		//print ans
		for(int i=0;i>n;
	dfs(1);
	return 0;
}

例题：递归实现排列型枚举 

#include
using namespace std;
int n,chosen[10],order[10],dep;
bool f[10];
void dfs(int dep){
	//检查边界；如果得到答案，就输出答案
	//如果说到了边界，还没得到答案，return 
	if(dep>n){
		for(int i=1;i<=n;i++)
			cout<< order[i]<<' ';
		cout<>n;
	dfs(1);
	return 0;
}

Day1练习题

蓝桥杯2013年第四届真题--带分数 

问题分析：

①递归解决排列问题

n=a+b/c
找1~9的排列     362880
在这个排列中加一个+再加一个/     64
计算符合条件的数量   2e7

时间复杂度过高会超时，蓝桥杯竞赛中允许的最高时间复杂度为1e8

②递归排列组合

n=a+b/c
n*c=a*c+b
b=c*n-a*c    只需要遍历两个未知数a和c即可确定未知数b

·枚举a ： 1~9里面先选数（递归解决指数型问题），再在选择的数中排列
·枚举c ：在剩下的数中选数，再在选择的数中排列
·确定b ：通过表达式b=c*n-a*c求值
·check ：
    看b是否合法（b当中的数字，是否包含了a和c选剩下的，而且没有和a，c重复的数字
    看等式是否成立

做题技巧：
1.排列123->整数123
    1 -> 1*10+2 -> 12*10+3 
2.整数123->排列123（检查b是否合法）

    int num;
    while(num){
        int n=num%10;
        num/=10;
    }

思路一 AC代码1：

#include
#include
#include
using namespace std;

int main(void){
	int a[]={1,2,3,4,5,6,7,8,9};
	int n,num=0;
	cin>>n;
	do{
		int num1,num2,num3;
		for(int i=1;i<8;i++){
			for(int j=i;j<8;j++){
				num1=num2=num3=0;
				for(int k=0;k

思路一 AC代码2：

#include
#include
using namespace std;
int num[9] = {1,2,3,4,5,6,7,8,9};
//分别代表 a b c 
int a ,b ,c ,n;
//获取在排列中l位置到r位置所得到的数字 
int getNum(int l,int r){
	int sum = 0; 
	for(int i=l ;i<=r ;i++){
		sum = sum*10+num[i];
	}
	return sum;
}
int main(){
	int ans = 0;
	scanf("%d",&n);
	do{
		//枚举a 
		for(int i=0 ;i<6 ;i++){
			a = getNum(0,i);
			if(a>n)break;
			if(a=c&&b%c==0&&(b/c+a)==n){
						ans++;	
					}
				}
			}
		}
	}while(next_permutation(num,num+9));
	printf("%d\n",ans);
	return 0;
}

思路二 AC代码：

#include
using namespace std;
int main(){

}

蓝桥杯往届试题：翻硬币

已知初始状态和要达到的目标状态，每次只能同时翻转两个相邻的硬币
只有偶数个不一样的时候才能达到目标状态
只要存在不一样的位置就必须翻
递推：一直往前走，只增不减

#include
#include
using namespace std;

string s1,s2;
int ans;
void fan(int i){
	if(s1[i]=='*') s1[i]='o';
	else if(s1[i]=='o') s1[i]='*';
}

int main(void){
	cin>>s1>>s2;
	
	//索引到倒数第二个，因为必须同时翻两个硬币
	for(int i=0;i

车厢重组（冒泡排序）

#include
using namespace std;
int N,a[10000],num=0,tem;
int main(void){
	cin>>N;
	for(int i=0;i>a[i];
	}
	
	for(int i=1;ia[j+1]){
				tem=a[j];
				a[j]=a[j+1];
				a[j+1]=tem;
				num++;
			}
		}
	}
	cout<

蓝桥杯2014年第五届真题：波动数列

#include
#define LL long long
#define MOD 100000007
using namespace std;
int main()
{
    LL n, s, a, b,sum_a,sum_b;
	LL dp[1010][1010] ;//dp[i][j] 代表序列前Ki的和取模n后的值为 j的方案数 
    cin>>n>>s>>a>>b;
    dp[1][(s%n+n)%n] = 1;//相当于式子的s%n，即 K1 ( (s%n+n) 是处理负数） 
    for (int i = 2; i<=n; i++){// 式子的前Ki项 
        sum_a = a*(n-i+1)%n;//假定 第i项为加上 a 那么 a 的贡献为 a*(n-i+1)%n 
        sum_b = b*(n-i+1)%n;//假定 第i项为减上 b 那么 b 的贡献为 b*(n-i+1)%n
        for (int j = 0; j < n; j++)//遍历所有前K(i-1)对n取模可能取到的值的方案数 
        {
            dp[i][(j-sum_a+n)%n] = (dp[i][(j-sum_a+n)%n] + dp[i-1][j]) % MOD;
        //前Ki项为j-sum_a对n取模的方案数 等于
		// 其它对n取模也得 j-sum_a值 加上 前K(i-1)项取模n的值j  (j-sum_a+n)防止负数 
            dp[i][(j+sum_b)%n] = (dp[i][(j+sum_b)%n] + dp[i-1][j]) % MOD;
        //前Ki项为j+sum_b对n取模的方案数 等于
		// 其它对n取模也得 j+sum_b值 加上 前K(i-1)项取模n的值j  
        }
    }
    cout<

母牛的故事

#include 
using namespace std;
int a[60];//开的稍微大一点
int main()
{
    int n;
    a[1] = 1;
    a[2] = 2;
    a[3] = 3;
    a[4] = 4;
    for(int i=5;i <= 60;i++)
        a[i] = a[i-1] + a[i-3];
    while(cin>>n && n != 0){
        cout<

明明的随机数

#include
using namespace std;
int a[10000],n,N,num=0;
int main(void){
	cin>>N;
	for(int i=1;i<=N;i++){
		cin>>n;
		a[n]=1;
	}
	for(int i=0;i<=1000;i++){
		if(a[i]==1) num++;
	}
	cout<

#include
#include

using namespace std;
int main()
{
	int tem;
	set a;
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>tem;
		a.insert(tem); //自动跳过已经存在的数 且插入时自动排序
	}
	cout<::iterator it; //set::iterator迭代器    it:集合中某一个数的地址 
	//迭代器：定义了一个it迭代器用来访问集合某个元素的地址
	for(it=a.begin();it!=a.end();it++)
	//a.begin()集合第一个数的地址
	//a.end()集合最后一个数的下一个地址
	cout<<*it<<' ';
	return 0;
}