组合数学进阶笔记

组合数学进阶

生成函数

生成函数及母函数。一共分为两类：普遍性函数、指数性函数。

普遍性函数

对于序列 $a_0,a_1,a_2,\dots$，定义 $G(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+\cdots +a_n{x}^n\dots$ 则称 $G(x)$ 是数列的生成函数。

指数性函数

生成函数是说，构造这么一个多项式函数 $g(x)$，使得 $x$ 的 $n$ 次方系数为 $f(n)$。

举个例子最清晰：

问：$x_1+x_2+\cdots +x_k=n$
问有多少种非负整数解？

解：令 $G(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+\cdots +a_n{x}^n\dots$

那么把题转化为 $G^k(x)$ 的 $n$ 次项的系数。

$G(x)=\frac{1}{1-x}(x<1)$

加一点小知识：

$\left(\begin{array}{c}n\\ k\end{array}\right)=\frac{n(n-1)(n-2)\dots (n-k+1)}{k!}$ 对于当 $n$ 为负数或小数时一样适用

运用二项式展开：

$n$ 次项系数为 $\left(\begin{array}{c}-n\\ k\end{array}\right)$，根据组合数定义：$n$ 次项系数为 $\left(\begin{array}{c}n+k-1\\ k-1\end{array}\right)$

P3711 仓鼠的数学题

设 $S_k(x)=\sum _{i=0}^x{i}^k$，给定正整数 $n$ 和序列 $a$，求：$\sum _{k=0}^n{S}_k(x)a_k$

数据范围：$1\le n\le 2\times 10^5$

解：

假设 $S_k(x)=\sum _{i=0}^{x-1}{i}^k$，之后只要把所有的 $x$ 换成 $x+1$ 即可，那么有

$S_k(x)=\frac{1}{k+1}\sum _{i=0}^k\left(\genfrac{}{}{0ex}{}{k+1}{i}\right)B_i{x}^{k+1-i}$

这个并不是很好看，所以考虑枚举 $k-i$ ：

$S_k(x)=\frac{1}{k+1}\sum _{i=0}^k\left(\genfrac{}{}{0ex}{}{k+1}{k-i}\right)B_{k-i}{x}^{i+1}$

利用二项式的对称性：

$S_k(x)=\frac{1}{k+1}\sum _{i=0}^k\left(\genfrac{}{}{0ex}{}{k+1}{i+1}\right)B_{k-i}{x}^{i+1}$

于是答案为

$\sum _{k=0}^n\frac{a_k}{k+1}\sum _{i=0}^k\left(\genfrac{}{}{0ex}{}{k+1}{i+1}\right)B_{k-i}{x}^{i+1}$

显然交换求和顺序

$\sum _{i=0}^n{x}^{i+1}\sum _{k=i}^n\frac{a_k}{k+1}\left(\genfrac{}{}{0ex}{}{k+1}{i+1}\right)B_{k-i}$

拆掉二项式

$\sum _{i=0}^n\frac{x^{i+1}}{(i+1)!}\sum _{k=i}^n{a}_{k}k!\frac{B_{k-i}}{(k-i)!}$

直接减法卷积即可，但是这里的 $x$ 实际上是 $x+1$，于是我们考虑下面的问题，求

$\sum _{i=0}^n{f}_i(x+1{)}^i$

直接利用二项式定理：

$\sum _{i=0}^n{f}_i\sum _{j=0}^i\left(\genfrac{}{}{0ex}{}{i}{j}\right)x^j$

交换求和顺序之后减法卷积即可。

Burnside引理、Polya定理

1.置换

置换简单来说就是对元素进行重排列，举个例子 $[1,n]$ 的置换是
$$\left(\begin{array}{ccccc}1& 2& 3& \dots & n\\ a_1& a_2& a_3& \dots & a_n\end{array}\right)$$

其中 $a_1,a_2,\dots a_n$ 就是对 $1,2,\dots n$ 的新排列

其实就是

#define 1 a_1
#define 2 a_2
...

2.Burnside引理

用 $D(a_j)$ 表示在置换 $a_j$ 下不变的元素的个数。$L$ 表示本质不同的方案数。

$L=\frac{1}{|G|}\sum _{j=1}^{s}D(a_j)$

对于刚才那个例子在 $N=4$ 的情况下的四种置换：
$$\left(\begin{array}{cccc}1& 2& 3& 4\\ 1& 2& 3& 4\end{array}\right)\left(\begin{array}{cccc}1& 2& 3& 4\\ 2& 3& 4& 1\end{array}\right)\left(\begin{array}{cccc}1& 2& 3& 4\\ 3& 4& 1& 2\end{array}\right)\left(\begin{array}{cccc}1& 2& 3& 4\\ 4& 1& 2& 3\end{array}\right)$$

所有方案在置换 $a_1$ 下都不变，$D(a_1)=16$

$XXXX$ 和 $EEEE$ 在置换 $a_2$ 下都不变，$D(a_2)=2$

$XXXX$ 和 $EEEE$ 以及 $XEXE$ 和 $EXEX$ 在置换 $a_3$ 下不变，$D(a_3)=4$

$XXXX$ 和 $EEEE$ 在置换 $a_4$ 下不变，$D(a_4)=2$

$\therefore L=\frac{1}{4}(16+2+4+2)=6$

Polya定理

我们发现要计算 $D(a_j)$ 很不容易，所以 Polya 老头就教我们了一个很好的办法。

我们先介绍一下循环的概念：

$(a_1{a}_2\dots a_n)=\left(\begin{array}{cccc}{a}_1& a_2& \dots & a_n\\ a_2& a_3& \dots & a_1\end{array}\right)$

例如：

$\left(\begin{array}{ccccc}1& 2& 3& 4& 5\\ 1& 3& 2& 4& 5\end{array}\right)=(23)(1)(4)(5)$

称为 $n$ 阶循环，置换的循环节数是上述的循环个数。

其实一个置换可以写成若干个不相交的循环的乘积，两个循环不相交的意思是循环 $(a_1{a}_2\dots a_n)$ 和 $(b_1{b}_2\dots b_n)$ 中 $a_i\ne b_j,i,j=1,2,\dots n$ 这样的表示是唯一的。

现在开始正式的 Polya 定理：

设 $G$ 是 $p$ 个对象的一个置换群，用 $m$ 种颜色涂染 $p$ 个对象，则不同的染色方案是：

$L=\frac{1}{|G|}(m^{c(g_1)}+m^{c(g_2)}+\cdots +m^{c(g_s)})$

其中 $G=\{g_1,g_2,\dots g_s\}$，$c(g_i)$ 为置换 $g_i$ 的循环节数 $(i=1,2,\dots s)$

继续举 Burnside 引理那个例子，我们给 $N=4$ 的环编号： $\begin{array}{cc}1& 2\\ 4& 3\end{array}$

构造一个置换群 $G^{\prime }=\{g_1,g_2,\dots g_s\}$，$|G^{\prime }|=4$ 令 $g_i$ 的循环节数为 $c(g_i)(i=1,2,3,4)$，在 $G^{\prime }$ 的作用下，其中：

$g_1$ 表示转 $0^{\circ }$ 即 $g_1=(1)(2)(3)(4),c(g_1)=4,2^{c(g_1)}=2^4=16=D(a_1)$

$g_2$ 表示转 $90^{\circ }$ 即$g_2=(4321),c(g_2)=1,2^{c(g_2)}=2^1=2=D(a_2)$

$g_3$ 表示转 $180^{\circ }$ 即 $g_3=(13)(24),c(g_3)=2,2^{c(g_2)}=2^2=4=D(a_3)$

$g_4$ 表示转 $270^{\circ }$ 即 $g_4=(1234),c(g_4)=1,2^{c(g_4)}=2^1=2=D(a_4)$

P6597 烯烃计数

有两种点 C 和 H，每个 C 点和每个 H 点都是相同的，即无标号。求满足以下条件的不同无向图的个数：

由 C 点和 H 点组成。

C 点个数 $n$，H点个数 $2n$。

每个 C 点度数为 $4$，每个 H 点度数为 $1$。

$1\le n\le 1000001$

解：

把碳-碳双键看作关键边,断开这条关键边,两边分别是一棵根节点的子节点个数 $\le 2$,除根节点外子节点个数 $\le 3$ 的无标号有根树

先用 Burnside 引理求出这棵树的方案再合并即可

设 $n$ 个点的烷基计数的普通生成函数为 $A(x)$,要求的树的普通生成函数为 $P(x)$

$P(x)=x\frac{A(x{)}^2+A(x^2)}{2}$

设答案的普通生成函数为 $Q(x)$

$Q(x)=\frac{(P(x)-1{)}^2+P(x^2)-1}{2}$

莫比乌斯反演

简化计算的一个好东东。

$F(n)$ 和 $f(n)$ 是定义在非负整数集上的两个函数，并且 $F(n)=\sum _{d|n}f(d)$ 那么：

$f(n)=\sum _{d|n}\mu (d)F(\frac{n}{d})$

$\mu$ 的定义如下：

1. 若 $d=1,\mu (d)=1$

2. 若 $d=p_1{p}_2\dots p_k$,$p_i$ 均为互异素数，$\mu (d)=(-1{)}^k$

3. 其他情况：$\mu (d)=0$

$\mu$ 函数有几个性质：

1.$\forall n\in Z^{+},\sum _{d|n}\mu (d)=\{\begin{array}{ll}1& n=1\\ 0& n>1\end{array}$

2.$\forall n\in Z^{+},\sum _{d|n}\frac{\mu (d)}{d}=\frac{\varphi (n)}{n}$

证明：

$f(n)=\sum _{d|n}\mu (d)F(\frac{n}{d})=\sum _{d|n}\mu (d)\sum _{k|\frac{n}{d}}f(k)=\sum _{k|n}f(k)\sum _{d\frac{n}{k}}\mu (d)$

$\because {\sum }_{d|n}\mu (d)=\{\begin{array}{ll}1& n=1\\ 0& n>1\end{array}$

$\therefore when\frac{n}{k}=1$就是$ n == k$,$\displaystyle\sum_{d|\frac{n}{k}}\mu(d)=1$,其余时候为$0$

也就搞出来了

P6810 Convex Hull 凸包

求：$\sum _{i=1}^n\sum _{j=1}^m\tau (i)\tau (j)\tau (\gcd (i,j))$

$\tau$ 表示约数个数，比如 $\tau (6)=4$

$1\le n,m\le 2\times 10^6,1\le p\le 10^9$

解：

原式 $$\begin{gathered} =\sum _{d=1}^{\min (n,m)}\tau (d)\sum _{i=1}^n\sum _{j=1}^m[\gcd (i,j)=d]\tau (i)\tau (j) \\ =\sum _{d=1}^{\min (n,m)}\tau (d)\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{m}{d}\rfloor }[\gcd (i,j)=1]\tau (id)\tau (jd) \\ =\sum _{d=1}^{\min (n,m)}\tau (d)\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{m}{d}\rfloor }\tau (id)\tau (jd)\sum _{q|\gcd (i,j)}\mu (q) \\ =\sum _{d=1}^{\min (n,m)}\tau (d)\sum _{q=1}^{\lfloor \frac{\min (n,m)}{d}\rfloor }\mu (q)\sum _{i=1}^{\lfloor \frac{n}{dq}\rfloor }\sum _{j=1}^{\lfloor \frac{m}{dq}\rfloor }\tau (idq)\tau (jdq) \\ =\sum _{d=1}^{\min (n,m)}\tau (d)\sum _{q=1}^{\lfloor \frac{\min (n,m)}{d}\rfloor }\mu (q)\sum _{i=1}^{\lfloor \frac{n}{dq}\rfloor }\tau (idq)\sum _{j=1}^{\lfloor \frac{m}{dq}\rfloor }\tau (jdq) \\ =\sum _{d=1}^{\min (n,m)}\tau (d)\sum _{q=1}^{\lfloor \frac{\min (n,m)}{d}\rfloor }\mu (q)\sum _{dq|i}^n\tau (i)\sum _{dq|j}^m\tau (j) \end{gathered}$$

预处理 $\mu$ 和 $\tau$ 函数的值，然后直接计算即可。

卡特兰数

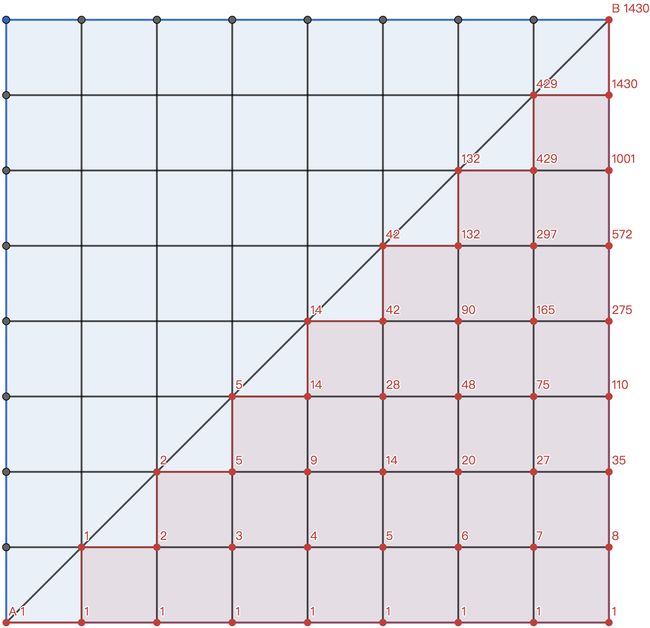
卡特兰数就是如图从A走到B并且不穿过那根红线的方法数。
运用表述法求出了几个值。

第 $n$ 个卡特兰数便是在 $n\times n$ 的方格中，从左下角走到右上角的方法数。

记：$C_n$ 为第 $n$ 个卡特兰数，如果我们假设 $C_0=1,C_1=1$ 那么，可得 $C_{n+1}=C_0{C}_n+C_1{C}_{n-1}+\cdots +C_n{C}_0$，它的通项公式为 $C_n=\frac{(2n)!}{(n+1)!\times n!}(n\ge 2)$

P2532 [AHOI2012]树屋阶梯

在一个 $n\times n$ 的图形中，用n个长方体填充，没有空缺和重复，问有几种方法？

在n=3时已给出：

$1\le n\le 500$

解：

我们发现对于任何大小为 $i$ 的树屋阶梯，都可以由左上角放一块大小为 $j$ 的以及右下角放一块大小为 $i-j-1$ 的树屋阶梯，再在空缺的地方由单个大块的矩形填充即可构成，这个构成的树屋阶梯一共有 $(j)+(i-j-1)+1$ 个钢材，正好是 $i$ 个。因为 $j$ 可以在 $0$ 到 $i-1$ 取且可以证明每一个构成的树屋阶梯一定各不相同，所以我们可以得到树屋阶梯方案与大小关系的递推式 $f_i=f_{i-1}{f}_0+f_{i-2}{f}_1\dots f_0{f}_{i-1}$。同时，我们规定 $f_0=f_1=1$。这不就是卡特兰数吗。

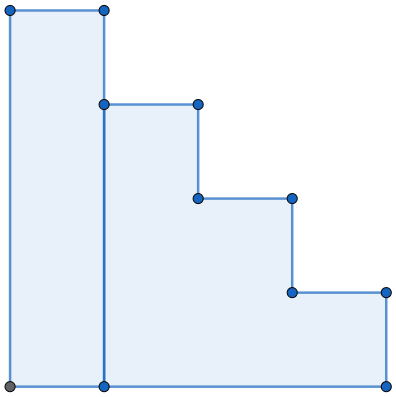
举个例子，我们可以怎么构成大小为 $4$ 的树屋阶梯呢？首先有第 $1$ 种构成方法：在左上角放上 $1$ 个任意大小为 $0$ 的树屋阶梯，在右下角放上 $1$ 个任意大小为 $3$ 的树屋阶梯，并在左下角的空缺用单个矩形填充。如图下所示：

这种构成方法下，我们能构成可行的树屋阶梯 $f_0\times f_3=1\times 5=5$ 个。

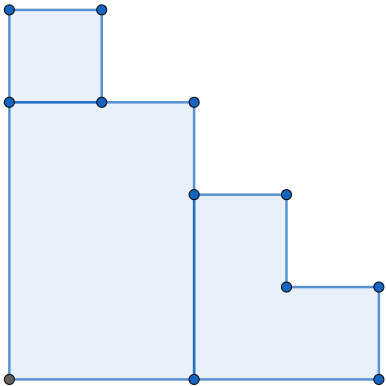
第 $2$ 种构成方法：在左上角放上 $1$ 个任意大小为 $1$ 的树屋阶梯，在右下角放上 $1$ 个任意大小为 $2$ 的树屋阶梯，并在左下角的空缺用单个矩形填充。如图下所示：

这种构成方法下，我们能构成可行的树屋阶梯 $f_1\times f_2=1\times 2=2$个。

类似地，还有 $2$ 种构成方法，本质上是和上面的 $2$ 种构成方法是一样的。所有方案数加在一起，得 $f_4=14$，正是卡特兰数了。所以直接卡特兰通项公式一下，要使用高精。

斯特林数

第一类

将n个元素排成k个轮换，记作 $\left[\begin{array}{c}n\\ k\end{array}\right]$，读作“$n$ 轮换 $k$”。可以把轮换想成一个环，写成 $[A,B,C,D]$ 把它理解为 $[A,B,C,D]=[B,C,D,A]=[C,D,A,B]=[D,A,B,C]$ 但是 $[A,B,C,D]\ne [A,B,D,C]\ne [D,C,B,A]$

将 $4$ 分成两个轮换：$[1,2,3][4],[1,2,4][3],[1,3,4][2],[2,3,4][1],[1,3,2][4],[1,4,2][3],[1,4,3][2],[2,4,3][1],[1,2][3,4],[1,3][2,4]$

$\therefore \left[\begin{array}{c}4\\ 2\end{array}\right]=11$

很容易看出来 $\left[\begin{array}{c}n\\ 1\end{array}\right]=\frac{n!}{n}=(n-1)!$，$\left[\begin{array}{c}n\\ n\end{array}\right]=1$，
$\left[\begin{array}{c}n\\ n-1\end{array}\right]=\left(\begin{array}{c}n\\ 2\end{array}\right)$

给个递归式：$\left[\begin{array}{c}n\\ k\end{array}\right]=(n-1)\left[\begin{array}{c}n-1\\ k\end{array}\right]+\left[\begin{array}{c}n-1\\ k-1\end{array}\right]$

$\ \ $

$\ \ $

$\ \ $

$\ \ $

P5408 第一类斯特林数·行

按顺序输出$\left[\begin{array}{c}n\\ 0\end{array}\right],\left[\begin{array}{c}n\\ 1\end{array}\right],\left[\begin{array}{c}n\\ 2\end{array}\right],\dots ,\left[\begin{array}{c}n\\ n\end{array}\right]$的值。

$1⩽n<262144$

解：

第 $n$ 行第一类斯特林数的生成函数为

$x^{\overline{n}}=\prod _{i=0}^{n-1}(x+i)=\sum _{i=0}^n\left[\begin{array}{c}n\\ i\end{array}\right]x^i$

所以我们只需要求出那个连续乘积就好了
考虑倍增。

$x^{\overline{2n}}=x^{\overline{n}}(x+n{)}^{\overline{n}}$
也就是

$\prod _{i=0}^{2n-1}(x+i)=\prod _{i=0}^{n-1}(x+i)\prod _{i=0}^{n-1}(x+n+i)$

那么只要能给定一个 $n$ 次多项式 $f(x)$，快速计算出 $f(x+k)$ 就行。

为了方便下面表述，我们设 $a_i=[x^i]f(x)$

$$\begin{gathered} f(x+k)=\sum _{i=0}^n{a}_i(x+k{)}^i \\ =\sum _{i=0}^n{a}_i\sum _{j=0}^i(\genfrac{}{}{0ex}{}{i}{j})x^j{k}^{i-j} \\ =\sum _{i=0}^n{x}^i\sum _{j=i}^n(\genfrac{}{}{0ex}{}{j}{i})k^{j-i}{a}_j \\ =\sum _{i=0}^n\frac{x^i}{i!}\sum _{j=i}^n\frac{k^{j-i}}{(j-i)!}j!a_j \end{gathered}$$

这个式子是卷积，下面演示一下为什么

设$g(x)=\sum _{i=0}^n\frac{k^i}{i!}{x}^{n-i}$

$h(x)=\sum _{i=0}^{n}i!a_i{x}^i$

那么只需要将 $g(x)$ 和 $h(x)$ 乘起来，然后左移n位(也就是将i次项系数变为 $n+i$ 次项系数)之后，第i次都乘上 $i!$ 就是我们想要的 $f(x+k)$ 了。

当然，倍增过程中还要有计算 $x^{\overline{n}}(x+n)$ 的情况，暴力线性算一下即可。

时间复杂度 $T(n)=T(n/2)+\Theta (n\log n)=\Theta (n\log n)$

P5409 第一类斯特林数·列

按顺序输出 $\left[\begin{array}{c}0\\ k\end{array}\right],\left[\begin{array}{c}1\\ k\end{array}\right],\left[\begin{array}{c}2\\ k\end{array}\right],\dots ,\left[\begin{array}{c}n\\ k\end{array}\right]$ 的值。

$1⩽k,n<131072$

解：

首先，我们可以对 $k=1$ 的情况构造指数级生成函数，即:

$S(x)={\sum }_{i=0}^n(i-1)!\frac{x^i}{i!}$

因为很显然 $\left[\begin{array}{c}n\\ 1\end{array}\right]=(n-1)!$。

那么，我们就可以得到，对于kk为任意数情况的指数级生成函数就是 $\frac{S(x{)}^k}{k!}$

除以 $k!$ 的主要原因是我们用指数级生成函数的环排列其实是有顺序。就比如 $[2,3,1][1,2]$ 和 $[1,2][2,3,1]$ 是等价的，但是我们算重了。

上面这个式子如果要美观一点就是:

$\frac{(\ln \frac{1}{1-x}{)}^k}{k!}$

这个可以通过泰勒展开得到。

时间复杂度：$O(n\log n)$

第二类

将一个有 $n$ 件物件的集合分成k个非空子集的方法数。记作 $\left\{\begin{array}{c}n\\ k\end{array}\right\}$，读作 $n子集k$

举个例子：将 $4$ 个元素的集合分为两个部分：
$\{1,2,3\}\cup \{4\},\{1,2,4\}\cup \{3\},\{1,3,4\}\cup \{2\},\{2,3,4\}\cup \{1\},\{1,2\}\cup \{3,4\},\{1,3\}\cup \{2,4\},\{1,4\}\cup \{2,3\}$

$\therefore \left\{\begin{array}{c}4\\ 2\end{array}\right\}=7$

用容斥原理可以推出 $\left\{\begin{array}{c}n\\ k\end{array}\right\}=\frac{1}{k!}\sum _{i=0}^{k-1}(-1{)}^i\left(\begin{array}{c}r\\ i\end{array}\right)(r-i{)}^n$

P5395 第二类斯特林数·行

按顺序输出 $\left\{\begin{array}{c}n\\ 0\end{array}\right\},\left\{\begin{array}{c}n\\ 1\end{array}\right\},\left\{\begin{array}{c}n\\ 2\end{array}\right\},\dots ,\left\{\begin{array}{c}n\\ n\end{array}\right\}$ 的值。

$1⩽n⩽2\times 10^5$

解：

通项就是一个卷积式，直接预处理阶乘逆元，打快速幂板子，NTT即可.

P5396 第二类斯特林数·列

按顺序输出 $\left\{\begin{array}{c}0\\ k\end{array}\right\},\left\{\begin{array}{c}1\\ k\end{array}\right\},\left\{\begin{array}{c}2\\ k\end{array}\right\},\dots ,\left\{\begin{array}{c}n\\ k\end{array}\right\}$ 的值。

$1⩽k,n<131072$

解：

考虑第 $k$ 列斯特林数的生成函数

$F_k(x)=\sum _i\left\{\begin{array}{c}i\\ k\end{array}\right\}{x}^i$

众所周知

$\left\{\begin{array}{c}i\\ k\end{array}\right\}=k\left\{\begin{array}{c}i-1\\ k\end{array}\right\}+\left\{\begin{array}{c}i-1\\ k-1\end{array}\right\}$

于是

$\begin{array}{rl}{F}_k(x)& =\sum _i\left(k\left\{\begin{array}{c}i-1\\ k\end{array}\right\}+\left\{\begin{array}{c}i-1\\ k-1\end{array}\right\}\right)x^i\\ & =\left(\sum _{i}k\left\{\begin{array}{c}i-1\\ k\end{array}\right\}{x}^i\right)+\left(\sum _i\left\{\begin{array}{c}i-1\\ k-1\end{array}\right\}{x}^i\right)\\ & =\left(kx\sum _i\left\{\begin{array}{c}i\\ k\end{array}\right\}{x}^i\right)+\left(x\sum _i\left\{\begin{array}{c}i\\ k-1\end{array}\right\}{x}^i\right)\\ & =kx{F}_k(x)+x{F}_{k-1}(x)\end{array}$

移项后可以得到

$F_k(x)=\frac{x{F}_{k-1}(x)}{1-kx}$

边界就是 $F_0(x)=1$

于是把上面那玩意儿一直展开下去，可以得到

$F_k(x)=\frac{x^k}{{\prod }_{i=1}^k(1-ix)}$

分治乘搞出分母，然后求逆在乘上 $x^k$ 就好了