BRDF详解（包括：irradiance，radiance，intensity，立体角）

 BRDF

        BRDF是双向反射分布函数（Bidirectional Reflectance Distribution Function，BRDF）用来定义给定入射方向上的辐射照度（irradiance），如何影响给定出射方向上的辐射率（radiance）。更笼统地说，它描述了入射光线经过某个表面反射后如何在各个出射方向上分布。也可理解为：光线从某个方向入射到表面后，能量被该表面吸收，然后再朝着各个方向发射出去。

 

 即 ：radiance/irradiance

---

 漫反射BRDF

 在光栅化的时候我们就已经了解到漫反射：光线在击中场景中的某点后会朝着四面八方均匀地散射出去。

 因此，漫反射的BRDF一定是一个常数。假设入射光是均匀且遍布整个半球方向，可以得到如下方程：

 （根据定义dw=sinθdθdϕ， 积分过程省略） 由于假设入射光是均匀且遍布整个半球方向，所以Li与方向无关，且等于Lo，最终约去两边L，得到结果：

但有一点要注意的是，这里并没有考虑能量被吸收，将反射率考虑进来之后，得到最终的漫反射BRDF：

 这里的ρ可以类比光栅化当中的漫反射系数去理解，本质就是一个3维向量，含有物体表面的颜色信息。

---

 镜面反射BRDF（微表面模型）

 漫反射项的形式简单且比较容易理解，但是对于镜面反射项，其形式则要更加高级一点：

 其中v为反射方向(观察方向)，l为入射方向，n为宏观表面法向，h为微平面法向

分子上的D,F,G为3个不同的函数：

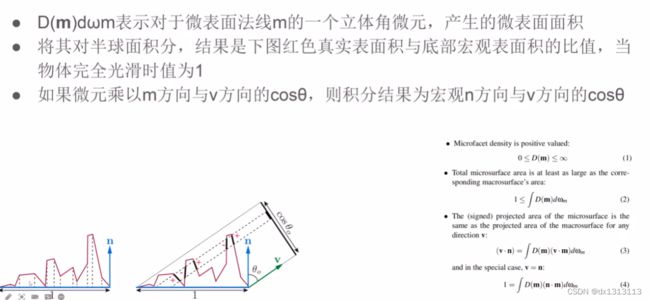
函数D：法线分布函数(Normal Distribution Function)，其代表了所有微观角度下微小镜面法线的分布情况，粗糙表面法线分布相对均匀，光滑表面法线分布相对集中 (这种解释可能会有些抽象，后面会给出更加直观的物理上的解释)

函数G：几何函数(Geometry Function)，描述了微平面自遮挡的属性。当一个平面相对比较粗糙的时候，平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。

函数F：菲涅尔方程(Fresnel Rquation)，描述了物体表面在不同入射光角度下反射光线所占的比率

 可以看出无论是几何函数G，还是菲涅尔方程F，都是由于观察方向，入射方向的不同所导致的只有部分光线能够被反射

分布概率密度D

 菲涅尔项F

反射irradiance/入射radiance(反射程度)

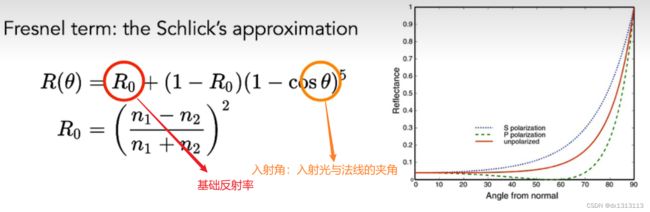
菲涅尔方程是为了描述物理世界当中，观察角度与法线夹角越大反射程度一般越大的一种情形，但是精确计算计算消耗较大，一般用Fresnel-Schlick近似法求得近似解

F0 表示平面的基础反射率，它是利用所谓折射系数(Indices of Refraction)计算得出的。越是朝球面掠角的方向上看（此时视线和表面法线的夹角接近90度）菲涅尔现象就越明显，反光就越强。但是根据折射系数只能算出电介质(非导体)的F0为了兼容导体，一般会将F0提前计算出来，再代入方程：

 几何函数G

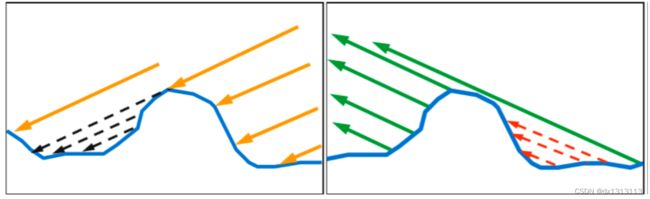
几何函数G是为了表示微平面的自遮挡从而引起的光线损失，一般会出现如下两种的遮挡情况

左边一幅图中是入射光线无法照射到一些微平面，这种情况称为Shadowing，右边图中是反射光线无法正常到达人眼，称为Masking，而几何函数G正是为了模拟出这两种情况所导致的光线所示，在UE4中采用了Schlick-GGX来进行建模：

---

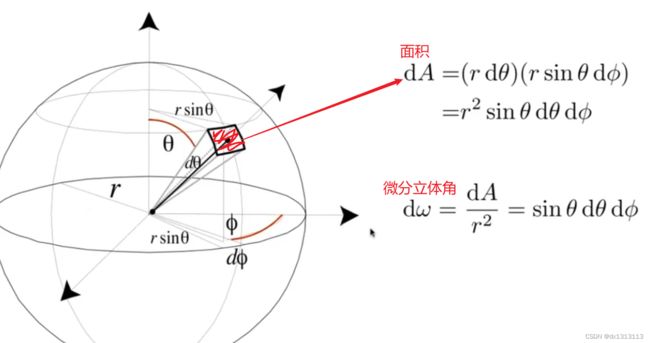
 微分立体角

        以观测点为球心，构造一个单位球面；任意物体投影到该单位球面上的投影面积，即为该物体相对于该观测点的立体角。因此，立体角是单位球面上的一块面积，这和“平面角是单位圆上的一段弧长”类似。

---

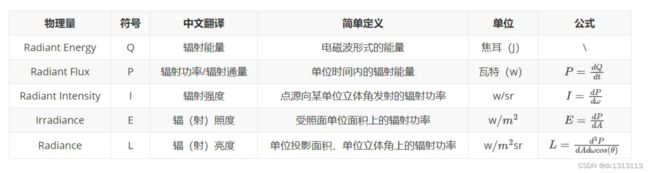
 辐射度量学相关概念

 强烈推荐的一个可视化网站

---

Irradiance

         辐射照度（irradiance）：单位面积接收到的辐射通量，称为该处的辐照度。符号为E，单位为W/m2。如果是单位光谱波长上的，单位为W/m2.μm。海洋光学中常用单位为W/cm2.nm或mW/cm2.μm。

注意： (这里的单位面积指的是和入射光线相垂直的面，若该面与入射光线不垂直则需要进行一个垂直的映射) eg:

        因此我们可以更深刻地解读出，某个单位面积接收到的能量与该位置距离点光源的距离的平方成反比，即irradiance随着距离增加而衰减。（这里认为点光源往空间中的各个方向均匀地辐射出能量）

---

Radiance

         辐亮度(radiance)：单位投影面积、单位立体角上的辐射通量。辐亮度的符号为L，单位为W/m2.sr，如果是单位光谱波长上的，单位为W/m2.um.sr。海洋光学中常用单位为W/cm2.nm.sr或mW/cm2.um.sr。

---

Irradiance:单位面积接收到的辐射能量

Intensity: 单位立体角接收到的辐射能量

Radiance：单位投影面积，单位立体角接收到文档辐射能量

所以：radiance可以看成 单位立体角的Irradiance、单位面积的Intensity：

---

Irradiance vs radiance

        Irradiance为某个单位面积上接收（发出）到的来自所有方向的辐射能量，radiance为该面积接收（发出）的朝某个单位立体角的辐射能量，因此Irradiance可看做对所有单位立体角的radiance的积分。

---

参考视频