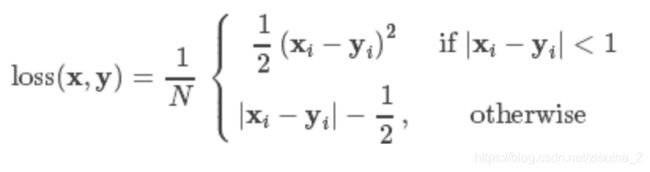深度学习基础loss和目标检测loss总结

深度学习Loss总结–目标检测：

• 一　基础loss
• 二　经典loss
• 三　旋转框的目标检测loss

检测的结构：主要看看loss的使用位置，以及它的意义；（ＯＫ，啥也没看出来）

一　基础loss

1. nn.L1Loss

loss_fn = torch.nn.L1Loss(reduce=False, size_average=False)

文章的最下方会解释什么是鲁棒，稳定解等

2 nn.smoothL1Loss

criterion = nn.SmoothL1Loss()
loss = criterion(sample, target)
print(loss)

3 nn.MSELoss

meanSquareError：就是平方差的loss; 在逻辑回归问题中，常常使用MSE（Mean Squared Error）作为loss函数

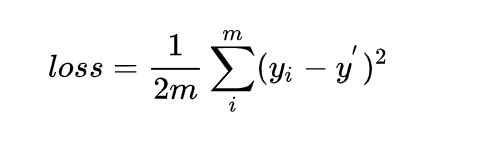
这里的y_i就表示期望输出，y_i’表示原始的实际输出（就是还没有加softmax)。这里的m表示有m个样本，loss为m个样本的loss均值。MSE在逻辑回归问题中比较好用，那么在分类问题中还是如此么？我们来看看Loss曲线。

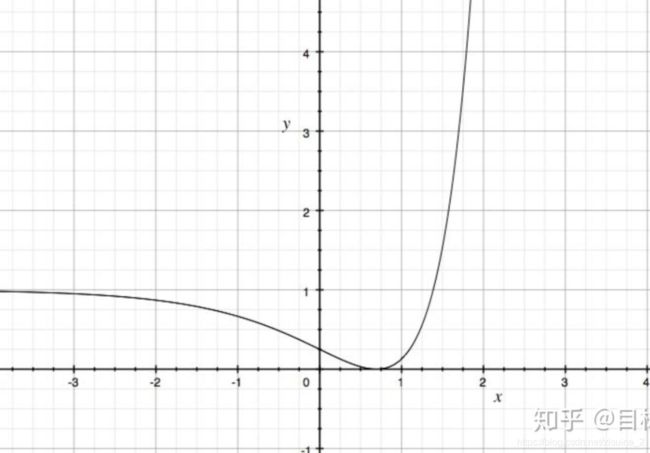
这是一个非凸函数,只有当损失函数为凸函数时，梯度下降算法才能保证达到全局最优解。所以MSE在分类问题中，并不是一个好的loss函数。

3 nn.BCELoss

二分类用的交叉熵，其计算公式较复杂，这里主要是有个概念即可，一般情况下不会用到。
离散版本：

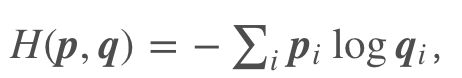
p是真实值；q为预测值；
这个以后在别的目标检测中，如focs就对其进行了修改；还是很有用的；

import torch.nn.functional as F
import torch
from torch.autograd import Variable
loss_fn = torch.nn.BCELoos(reduce = False, size_average= False)
input = Variable(torch.randn(3,4))
target = Variable(torch.FloatTensor(3,4).random_(2))
loss = loss_fn(F.sigmoid(input),target)
print(loss)

参数：

**

1. weight (Tensor,可选)– a manual rescaling weight given to the loss of each batch element. If given, has to be a Tensor of size “nbatch”.每批元素损失的手工重标权重。如果给定，则必须是一个大小为“nbatch”的张量。
2. size_average (bool, 可选) –
   弃用(见reduction参数)。默认情况下，设置为True，即对批处理中的每个损失元素进行平均。注意，对于某些损失，每个样本有多个元素。如果字段size_average设置为False，则对每个小批的损失求和。当reduce为False时，该参数被忽略。默认值:True
3. reduce (bool,可选) –
   弃用(见reduction参数)。默认情况下，设置为True，即根据size_average参数的值决定对每个小批的观察值是进行平均或求和。如果reduce为False，则返回每个批处理元素的损失，不进行平均和求和操作，即忽略size_average参数。默认值:True
4. reduction (string,可选) – 指定要应用于输出的reduction操作:’ none ’ | ‘mean’ | ’
   sum
   '。“none”:表示不进行任何reduction，“mean”:输出的和除以输出中的元素数，即求平均值，“sum”:输出求和。注意:size_average和reduce正在被弃用，与此同时，指定这两个arg中的任何一个都将覆盖reduction参数。默认值:“mean”

4 nn.CrossEntropyLoss

交叉熵损失函数，这个可以支持多分类

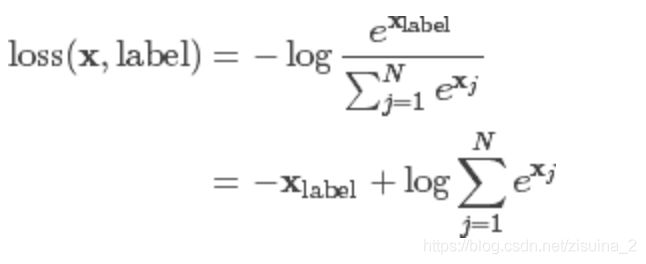
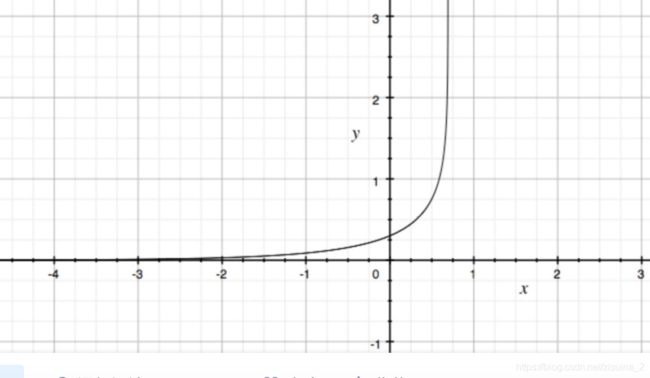
CrossEntropyLoss相对MSE而言，曲线整体呈单调性，loss越大，梯度越大。便于梯度下降反向传播，利于优化。所以一般针对分类问题采用交叉熵作为loss函数。

import torch
import torch.nn as nn
import math

criterion = nn.CrossEntropyLoss()
output = torch.randn(1, 5, requires_grad=True)
label = torch.empty(1, dtype=torch.long).random_(5)
loss = criterion(output, label)
print(loss)

5 nn.NLLLoss

用于多分类的负对数似然损失函数（Negative Log Likelihood）

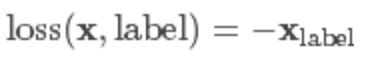
在前面接上一个 LogSoftMax 层就等价于交叉熵损失了。注意这里的 xlabel 和上个交叉熵损失里的不一样，这里是经过 log 运算后的数值。这个损失函数一般也是用在图像识别模型上。

import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(2019)
output = torch.randn(1, 3)  # 网络输出
target = torch.ones(1, dtype=torch.long).random_(3)  # 真实标签
criterion = nn.NLLLoss()
loss = criterion(output, target)
print(loss)
print(loss)

二　经典目标检测loss

上面讲了很多基础的loss,这些都会出现于各种问题中,loss这玩意还是需要针对不同问题进行解决的；我们主要来看看目标检测的loss总结；目标检测的LOSS很多都是不同的分支使用不同的loss，最后进行求和．主要是两部分：１．分类的分支，２．Iou分支：基于anchor结构（或者长宽分支和中心点分支：基于centerness结构）；

6 yolov1 损失函数

这个loss主要分为3部分（这里是yolo1）
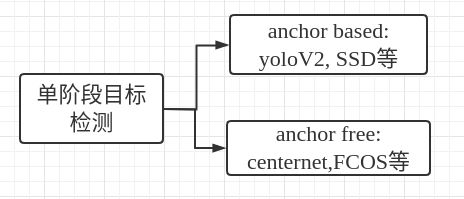
Yolo算法里的三个版本，YoloV1可以算作anchor-free类；YoloV2开始引入anchor，YoloV3也使用了anchor。
原文地址： https://arxiv.org/pdf/1506.02640.pdf

① 坐标误差
对不同大小的bbox预测中，相比于大bbox预测偏一点，小box预测偏一点更不能忍受。作者用了一个比较取巧的办法，就是将box的width和height取平方根代替原本的height和width

（主要为了平衡小目标检测预测的偏移）

② IOU误差（很多人不知道C_i代表什么）

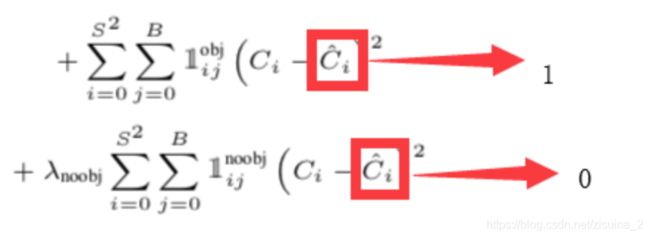
其实这里的分别表示 1 和 0

③ 分类误差

这个很容易理解（激活函数的输出）

可以发现，现在的loss已经不能只是简单一个原理组成的了；分了很多部分；

７ FCOS－－Facol loss

论文题目： FCOS: Fully Convolutional One-Stage Object Detection
原文地址： https://arxiv.org/abs/1904.01355

fcos整体的架构，主要看右边，三个分支：classification（ssnum_class）, centerness（ss1）, regression（ss4）分支;

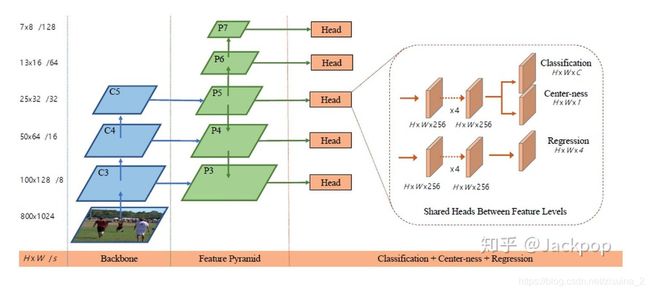
此处，centerness的分支计算方式为（这玩意训练中，想低低不下来…）：

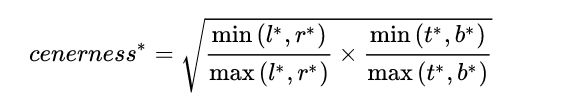
focal loss最初出自于retinanet,但也是centerness的loss形式；Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。

之前的交叉熵损失y’是经过激活函数的输出，就是预测值；所以在0-1之间。可见普通的交叉熵对于正样本而言，输出概率越大损失越小。对于负样本而言，输出概率越小则损失越小。此时的损失函数在大量简单样本的迭代过程中比较缓慢且可能无法优化至最优。
Focal loss是在交叉熵损失函数基础上进行的修改（注意y只有两个值：０，１）：

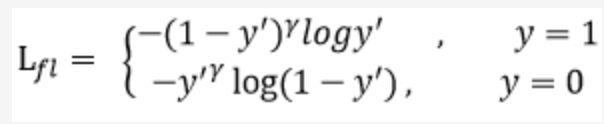
首先在原有的基础上加了一个因子，其中gamma>0使得减少易分类样本的损失。使得更关注于困难的、错分的样本。

例如gamma为2，对于正类样本而言，预测结果为0.95肯定是简单样本，所以（1-0.95）的gamma次方就会很小，这时损失函数值就变得更小。而预测概率为0.3的样本其损失相对很大。对于负类样本而言同样，预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时，损失只减少了0.25倍，所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。

８ CenterNet 的loss构成

CenterNet对于移动端设备非常友好，git上已经5000＋星星，牛逼．
原文：Objects as Points

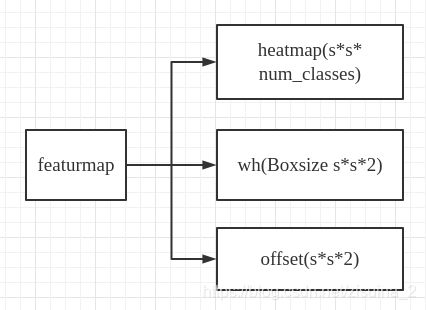
这里heatmap的Loss计算使用了focal loss来解决正负样本比例失衡的问题，因为以中心点提出的foreground和background是有失衡的．其余的wh和offset分支都是使用RegL1Loss进行的；

如下图Figure3, (a)是传统的基于anchor的正负样本选取，IOU>=0.7的为正样本，IOU<=0.3的为负样本；

b)是论文中提出的方法：此方法与基于锚点的onestage方法密切相关。一个中心点可以看作是一个单一的形状不可知的anchor。但是，有几个重要的区别。首先，这里的中心网分配“锚”完全基于位置，而不是框重叠（a）对于前景和背景分类，没有手动阈值（a）。其次，每个对象只有一个正“锚”，因此不需要非最大抑制(NMS)。这里只是提取关键点heatmap中的局部峰值。第三，CenterNet使用了较大的输出分辨率（输出stride为4）与传统的物体探测器（输出stride为16）相比。这就消除了对多个锚的需要。

以下降了对于对于heatmap的focal loss的使用，我觉的比较重要的部分；

我觉得这个讲的很好，引用［https://www.jianshu.com/p/0637a1ef46e1］

９ Generalized Focal Loss:

论文题目： Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
原文地址： https://arxiv.org/pdf/2006.04388.pdf

PCALab南京大学和微软2020发表的Generalized Focal Loss这篇就厉害了，它发现了，在inference和在train的时候,　inference的时候乘了iou LOSS，但是train的时候分类的分支和iou或者centerness的分支是相互独立训练的；所以导致了前后不一致；统一了训练和推理过程中的不一致问题；

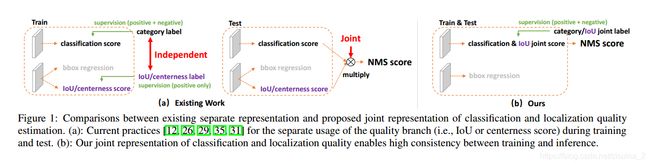
Generalized Focal Loss主要由：Quality Focal Loss (QFL)；Distribution Focal Loss (DFL)组成；
Quality Focal Loss (QFL):
之前的fl都是非０即１，这里，可以是０－１之间的概率；这里的y就是ＩＯＵ　LOSS的值；

Distribution Focal Loss (DFL)
这玩意还挺复杂的，就是将以前的bounding box的回归损失，使用分类的技巧，将回归问题变成分类问题；因为回归的东西很难收敛；

中心点到groundtruth四条边的距离使用了分段进行求分，每一层都是几段，最后使用softmax进行输出，来获得最终得分；具体的可以看论文，也有git: https://github.com/implus/GFocal

在我们的实验结果下，不同数据集的目标检测问题都提高了不错（　＾＿＾　）的点数，可以试一下哟．

10 IOU loss

论文题目： UnitBox: An Advanced Object Detection Network
原文地址： https://arxiv.org/pdf/1608.01471.pdf

IOU Loss是旷视在2016年提出的《UnitBox: An Advanced Object Detection Network》。该论文的主要观点之一是：
使用基于欧式距离的L-n损失函数，其前提是假设4个坐标变量都是独立的，但实际上，这些坐标变量是具有一定的关联性。
评价指标使用了IOU，而回归坐标框又使用4个坐标变量，这两者是不等价的。
具有相同的欧式距离的框，其IOU值却不是唯一的。
所以，提出了IOU loss，直接使用IOU作为损失函数：

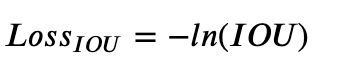
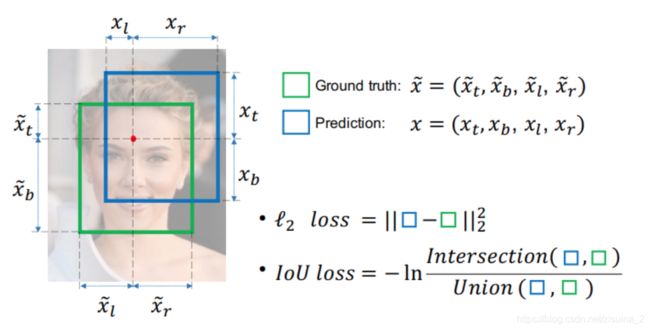
11 GIOU

论文题目： Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
原文地址： https://arxiv.org/pdf/1911.08287.pdf

该GIOU Loss损失函数是斯坦福于2019年提出的《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》。在上面的IOU Loss中，无法对两个不重叠的框进行优化，而且IOU Loss无法反映出两个框到底距离有多远。为了解决这个问题，作者提了GIOU来作为损失函数：

GIOU具有以下的性质：

• GIOU可以作为一种衡量距离的方式，=1−
• GIOU具有尺度不变性
• GIOU是IOU的下限，(,)≤(,)。当矩形框A、B类似时，lim→(,)=(,)
• 当矩形框A、B重叠时，(,)=(,)
• 当矩形框A、B不相交时，(,)=−1

总的来说，GIOU包含了IOU所有的优点，同时克服了IOU的不足。

def giou_loss(pred, target, eps=1e-7):
    """
    Generalized Intersection over Union: A Metric and A Loss for
    Bounding Box Regression
    https://arxiv.org/abs/1902.09630

    code refer to:
    https://github.com/sfzhang15/ATSS/blob/master/atss_core/modeling/rpn/atss/loss.py#L36

    Args:
        pred (Tensor): Predicted bboxes of format (x1, y1, x2, y2),
            shape (n, 4).
        target (Tensor): Corresponding gt bboxes, shape (n, 4).
        eps (float): Eps to avoid log(0).

    Return:
        Tensor: Loss tensor.
    """
    # overlap
    lt = torch.max(pred[:, :2], target[:, :2])
    rb = torch.min(pred[:, 2:], target[:, 2:])
    wh = (rb - lt + 1).clamp(min=0)
    overlap = wh[:, 0] * wh[:, 1]

    # union
    ap = (pred[:, 2] - pred[:, 0] + 1) * (pred[:, 3] - pred[:, 1] + 1)
    ag = (target[:, 2] - target[:, 0] + 1) * (target[:, 3] - target[:, 1] + 1)
    union = ap + ag - overlap + eps

    # IoU
    ious = overlap / union

    # enclose area
    enclose_x1y1 = torch.min(pred[:, :2], target[:, :2])
    enclose_x2y2 = torch.max(pred[:, 2:], target[:, 2:])
    enclose_wh = (enclose_x2y2 - enclose_x1y1 + 1).clamp(min=0)
    enclose_area = enclose_wh[:, 0] * enclose_wh[:, 1] + eps

    # GIoU
    gious = ious - (enclose_area - union) / enclose_area
    loss = 1 - gious
    return loss

12 DIOU和CIOU

论文题目： Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
原文地址：https://arxiv.org/pdf/2005.03572.pdf

DIOU和CIOU是天津大学于2019年提出的《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》。为了解决GIOU收敛慢和提高回归精度，提出DIOU来加速收敛。同时考虑到框回归的3个几何因素（重叠区域，中心点距离，宽高比），基于DIOU，再次提出CIOU，进一步提高收敛速度和回归精度。另外，可以将DIOU结合NMS组成DIOU-NMS，来对预测框进行后处理。

当出现下图的情况（GT框完全包含预测框）时，IOU与GIOU的值相同，此时GIOU会退化成IOU，无法区分其相对位置关系。同时由于严重依赖于IOU项，GIOU会致使收敛慢。

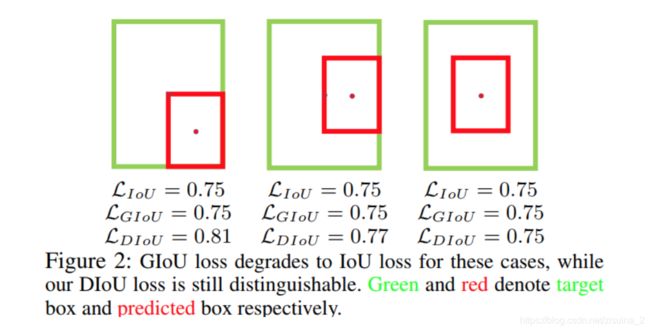
直接最小化预测框与目标框之间的归一化距离是否可行，以达到更快的收敛速度。
如何使回归在与目标框有重叠甚至包含时更准确、更快
好的目标框回归损失应该考虑三个重要的几何因素**：重叠面积，中心点距离，长宽比**。基于问题一，作者提出了DIoU Loss，相对于GIoU Loss收敛速度更快，该Loss考虑了重叠面积和中心点距离，但没有考虑到长宽比；针对问题二，作者提出了CIoU Loss，加入长宽比，其收敛的精度更高，以上三个因素都考虑到了。

所以，具有如下性质：

1. DIOU依然具有尺度不变性；
2. DIOU直接最小化两个框的距离，因此收敛会更快；
3. 对于目标框包裹预测框的这种情况，DIoU
   Loss可以收敛的很快，而GIoU Loss此时退化为IoU Loss收敛速度较慢

13 CIOU(Complete-IoU)

论文考虑到bbox回归三要素中的长宽比还没被考虑到计算中，因此，进一步在DIoU的基础上提出了CIoU：多考虑了长宽比。其惩罚项如下面公式：


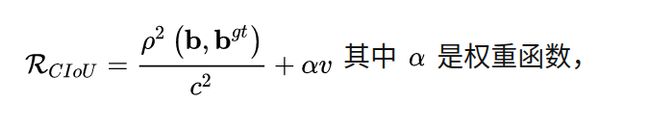
代码：

def bbox_overlaps_ciou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    cious = torch.zeros((rows, cols))
    if rows * cols == 0:
        return cious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        cious = torch.zeros((cols, rows))
        exchange = True

    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1]
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]

    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    u = (inter_diag) / outer_diag
    iou = inter_area / union
    with torch.no_grad():
        arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
        v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
        S = 1 - iou
        alpha = v / (S + v)
        w_temp = 2 * w1
    ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
    cious = iou - (u + alpha * ar)
    cious = torch.clamp(cious,min=-1.0,max = 1.0)
    if exchange:
        cious = cious.T
    return cious

测试用例

import torch
Cious2 = bbox_overlaps_ciou(torch.tensor([[ 300,  300,  400,  400]]),torch.tensor([[ 350,  350,  380,  380],
                                                                                        [ 400,  400, 500,  500],
                                                                                        [ 310,  310,  410,  410],
                                                                                        [280,  280,  330,  330]]) )

14 Focal and Efficient IOU Loss(EIOU)

论文：　Focal and Efficient IOU Loss for Accurate Bounding Box Regression
地址：　https://arxiv.org/abs/2101.08158

这论文就说啊，CIOU GIOU有问题，如下图，GIOU在迭代中，趋向于把预测框变成两个的∪集的框；CIOU在演变的过程中，不能保证长宽比；所以提出了ＥIOU，多考虑了长， 宽的单独项；


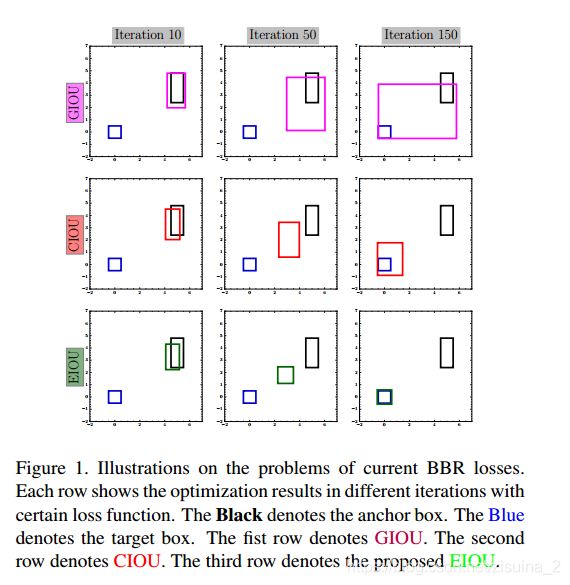
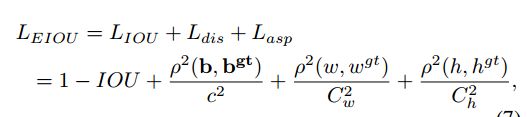
如上图所示：它比ＣＩＯＵ多出了两项：对长和宽的惩罚项，代码中是lasp；自己参悟吧，兄弟们；实验还在跑，也不知道是不是水文；毕竟在实验里，iou和giou的得分一样的，很奇怪啊！

def bbox_overlaps_focal_eiou(bboxes1, bboxes2, eps=1e-7):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    cious = torch.zeros((rows, cols))
    if rows * cols == 0:
        return cious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        cious = torch.zeros((cols, rows))
        exchange = True
    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1]
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]
    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
    inter_max_xy = torch.min(bboxes1[:, 2:], bboxes2[:, 2:])
    inter_min_xy = torch.max(bboxes1[:, :2], bboxes2[:, :2])
    out_max_xy = torch.max(bboxes1[:, 2:], bboxes2[:, 2:])
    out_min_xy = torch.min(bboxes1[:, :2], bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1) ** 2 + (center_y2 - center_y1) ** 2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2) + eps
    union = area1 + area2 - inter_area + eps
    u = (inter_diag) / outer_diag
    iou = inter_area / union

    cw_h = out_max_xy - out_min_xy

    lasp = (w1 - w2) ** 2 / (cw_h[:, 0] ** 2 + eps )+ (h1 - h2) ** 2 / (cw_h[:, 1] ** 2 + eps)

    cious = iou - (u + lasp)
    cious = torch.clamp(cious, min=-1.0, max=1.0)
    gious_loss = 1 - cious


    return gious_loss

15 Focal and Efficient IOU Loss(SIOU)

论文：https://arxiv.org/pdf/2205.12740.pdf
SIoU Loss: More Powerful Learning for Bounding Box Regression
Zhora Gevorgyan 2022
考虑了四方面的内容：

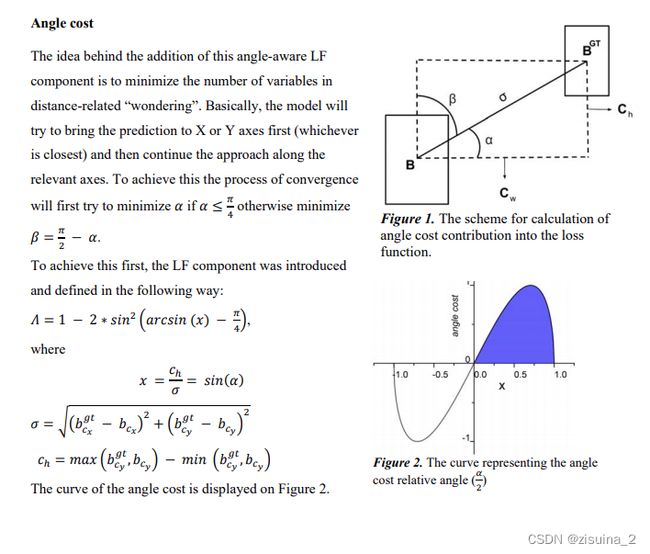
• 角度误差（如下图）
• 距离误差（CIOU 类似）具体论文
• 形状误差
• IOU误差

形状误差

def siou_loss(pred, target, eps=1e-7):
    b1_x1, b1_y1, b1_x2, b1_y2 = pred[:, 0], pred[:,1], pred[:,2], pred[:,3]
    b2_x1, b2_y1, b2_x2, b2_y2 = target[:,0], target[:,1], target[:,2], target[:,3]
    # Intersection area
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * (
            torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)
    ).clamp(0)

    # Union Area
    w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
    w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
    union = w1 * h1 + w2 * h2 - inter + eps
    iou = inter / union

    cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1)  # convex width
    ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1)  # convex height
    s_cw = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5
    s_ch = (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5
    sigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5)
    sin_alpha_1 = torch.abs(s_cw) / sigma
    sin_alpha_2 = torch.abs(s_ch) / sigma
    threshold = pow(2, 0.5) / 2
    sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)
    angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - math.pi / 2)
    rho_x = (s_cw / cw) ** 2
    rho_y = (s_ch / ch) ** 2
    gamma = angle_cost - 2
    distance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y)
    omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)
    omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)
    shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(
        1 - torch.exp(-1 * omiga_h), 4
    )
    iou = iou - 0.5 * (distance_cost + shape_cost)
    loss = 1.0 - iou
    return loss

Oriented bounding box 旋转bouding框的loss

旋转矩形的loss；有很多：＜Arbitrary-Oriented Object Detection with Circular Smooth Label＞ 很多，以后有空整理整理；

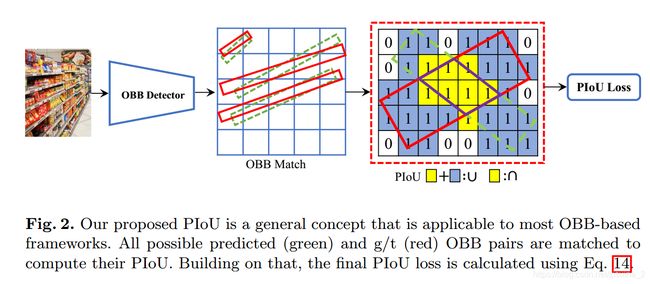
14 PIoU Loss

论文题目： PIoU Loss: Towards Accurate Oriented Object Detection in Complex Environments
原文地址：https://arxiv.org/pdf/2007.09584.pdf

以像素为单位，进行交并集的计算；
还有很多，不一一列举了，以后有空可以整理．