点云配准(四) Sparse Point Registration 算法浅析
Sparse Point Registration (SPR)是一篇2017年的点云配准算法,该算法的主要目的是对稀疏点云进行配准,并且取得了不错的成果和突破。本文一方面是对SPR配准算法模型进行了简单的原理解析以及附加代码实现,另一方面是对之前工作的总结,也算水篇博文,接下来的工作主要就是分割和光流预测方面的学习了。
一.算法模型概述
1.算法背景
所谓稀疏点云就是点数稀少的点云模型,有时我们需要用到一些物体上的关键点来和目标模型进行配准,计算一些关键指标。而传统的点云配准算法要求待配准的两片点云数量级相当,并且还包括粗配准和精配准两个阶段。经实验可得,传统点云配准算法在稀疏点云配准上表现较差,因此稀疏点云配准十分关键。
2.算法模型
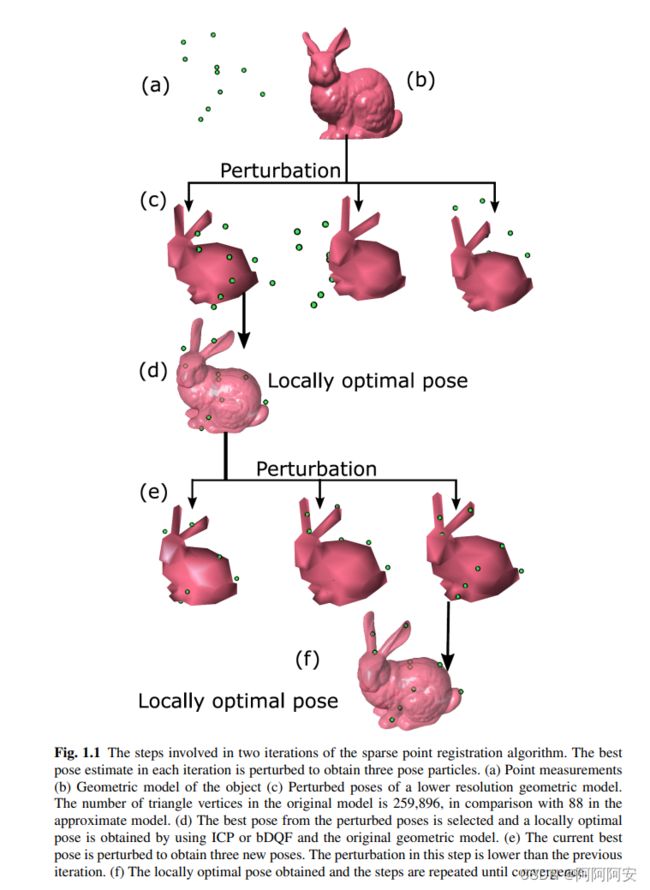
SPR算法不需要进行粗配准就可以实现效果较好的稀疏点云配准效果,该算法的核心思想主要包括扰动、迭代、细化三个部分。SPR算法模型包括以下步骤:
- 初始化目标模型点云数据A,稀疏点云数据B,最大迭代次数MaxIterations,配准误差阈值Threshold、扰动次数P
- 根据点云Size和高斯分布计算当前迭代的扰动量(扰动量随着迭代次数不断减小,最后减小到零)获取P个扰动扰动变换矩阵,然后对当前B点云进行扰动变换
- 分别计算P个扰动变换后的稀疏点云B和目标模型点云A的 Cost (这里可以使用K-D Tree 计算最近点偏差和作为Cost),选择Cost最小的作为局部最优扰动
- 基于当前的最优扰动变换后的稀疏点云B,进行 ICP or DQF 算法精配准细化(本文选择ICP),获得精配准矩阵Tk,并计算此时的误差
- 若计算的误差小于最小误差e,则更新全局最优边换矩阵T和最小误差e为当前迭代结果。
- 重复迭代以上过程,直到达到最大迭代次数MaxIterations或计算误差e<配准误差阈值Threshold
3.算法流程图
除此之外,论文中还阐释了一些比较细节的注意事项和参数设置,比如最大迭代次数MaxIterations、配准误差阈值Threshold、扰动次数P设置为多少,如何进行扰动计算,以及如何在试验中取点等等,当然稀疏点云中越具有特征性的关键点配准效果越好。
二.算法实现(ICP版本)
本文的SPR算法实现使用Matlab编程进行,采用ICP的精配准版本,在实现过程中对原算法进行了改进:在迭代过程中,对每一个出现的扰动变换都进行ICP精配准计算,然后基于这个误差进行比较,而不只是原算法所言的选出最优扰动后再计算ICP,这样可以最大程度的提高算法精确度,但是牺牲了时间复杂度。下面给出部分代码。
(1)SPR.m
% SPR Main logic function:transform A sparse point cloud into B model point cloud coordinate system for registration
% - Params:
% - A:sparse point cloud [n,3]
% - B:model point cloud [m,3]
% - Return:
% - R:optimal rotation matrix [3,3]
% - T:optimal translation matrix [1,3]
% - trans_res:transform point cloud [n,3]
function [ R,T,trans_res ] = SPR(A,B)
%1.kdtree model for B(euclidean distance) and size of the model
Mdl = KDTreeSearcher(B);
Size = max(range(B));
%2.Initialize R0,T0,e0
R = eye(3);
%Align the centroids of two point clouds A->B
cen_A = sum(A)/length(A);
cen_B = sum(B)/length(B);
T = cen_B - cen_A;
trans_res = transform(A,R,T);
e = calculateCost(trans_res,B,Mdl);
%3.Initialize the number of disturbed pose P, the maximum number of iterations I, and the minimum error threshold RMS
P = 10;
I = 30;
RMS = 1e-6;
%4.Initialize loop variable
k = 1;
%record data
x_loop = 1:I;
y_error = zeros(1,I);
%5.SPR Loop
while e > RMS && k <= I
cost_best = inf;
R_k = R;
T_k = T;
%(1). Perturbations for Sparse point cloud,and then the perturbation transformation matrix is obtained
% - R_p: [3,3,P+1]
% - T_p: [p+1,3]
[R_p, T_p] = perturb(Size,P,k,I);
%(2). Calculate the optimal pose
for j = 1:P+1
%Obtain the transformation matrix parameters rp_j(3,3), tp_j(1,3) of the current p-th disturbance pose
rp_j = R_p(:,:,j)*R;
tp_j = (R_p(:,:,j)*T')'+T_p(j,:);
%Calculate current optimal cost(from ICP)
[R_j,T_j,cost_j] = solveicp(A,B,Mdl,rp_j,tp_j);
%judge optimal cost
if cost_j < cost_best
cost_best = cost_j;
R_k = R_j;
T_k = T_j;
end
end
%(3). Error calculation and judge for update
trans_k = transform(A,R_k,T_k);
e_k = calculateCost(trans_k,B,Mdl);
if e_k < e
e = e_k;
R = R_k;
T = T_k;
end
y_error(k) = e;
k = k+1;
end
trans_res = transform(A,R,T);
figure
plot(x_loop,y_error,marker='o', MarkerFaceColor='r');
xlabel('loop');
ylabel('ems error');
end(2)Perturb.m
%Disturbance function: Generates random perturbations based on iteration within loop and specified
% - Params:
% - size:Size of the model
% - P:Number of disturbances
% - k:Number of iterations
% - I:Iteration upper bound
% - Return:
% - R_p:Perturbation rotation matrix [3,3,P+1]
% - T_p:Perturbation translation matrix [P+1,3]
function [ R_p, T_p ] = perturb( size,P,k,I )
%1.Initial translation disturbance:10% of the model size
T_p = normrnd(0,(0.1*size*((I+1-k)/I)),[P,3]); %[P,3]
%2.Initial perturbation number of rotation:10 ° normal distribution(Right hand coordinate system)
%Around x
a = normrnd(0,(10*((I+1-k)/I)),[1,P]); %[1,P]
%Around y
b = normrnd(0,(10*((I+1-k)/I)),[1,P]);
%Around z
c = normrnd(0,(10*((I+1-k)/I)),[1,P]);
%3.convert to radians
a = a.*(pi()/180);
b = b.*(pi()/180);
c = c.*(pi()/180);
%4.initialize R_p
R_p = zeros(3,3,P);
%5.Generate P disturbances respectively (matlab subscript starts from 1)
for j = 1:P
%rotation matrix about x
r1 = [1,0,0; 0, cos(a(j)), -sin(a(j)); 0, sin(a(j)), cos(a(j))];
%rotation matrix about y
r2 = [cos(b(j)), 0, sin(b(j)); 0,1,0; -sin(b(j)), 0, cos(b(j))];
%rotation matrix about z
r3 = [cos(c(j)), -sin(c(j)), 0; sin(c(j)), cos(c(j)), 0; 0,0,1];
%Perturbation Rotation
R_p(:,:,j) = r1*r2*r3;
end
%P+1:Transformation without disturbance
R_p(:,:,P+1) = eye(3);
T_p(P+1,:) = [0,0,0];
end
(3)solveicp.m
%Function takes in A and B clusters, registers A to B using ICP, returns resultant transformation matrix and error calculation
% - Params:
% - A:initial point cloud [n,3]
% - B:target point cloud [m,3]
% - Return:
% - TR:solve rotation matrix [1,3]
% - RO:solve translation matrix [3,3]
% - e:registers error
function [ R,T,e ] = solveicp( A,B,Mdl,R_0,T_0 )
%1.initialize variable parameters
k = 1;
error = 0.0001;
Iterator = 50;
R = R_0;
T = T_0;
%2.initial:kdtree algorithm to find the nearest point pair of two point clouds
trans = transform(A,R,T);
e = calculateCost(trans,B,Mdl);
%3.ICP loop
while e > error && k <= Iterator
%find the nearest point
idx = knnsearch(Mdl,trans);
NN = B(idx,:);
%svd solve: optimal matching matrix of two point clouds in current state
[T_k, R_k] = solvesvd(trans,NN);
%Cumulative transformation T=[1,3] R=[3,3]
T = (R_k*T')'+T_k;
R = R_k*R;
trans = transform(A,R,T);
%Update error E
e = sum(sqrt(sum((NN-trans).^2,2)))/length(trans);
k = k+1;
end
end
(4)solvesvd.m
%function: svd solve yo find T and R between point set B and it nearest neighbour set
% - Params:
% - B:initial point clouds [n,3]
% - NN: target nearest neighbour point clouds [n,3]
% - Return:
% - T:solve optimal translation matrix [1,3]
% - R:solve optimal rotation matrix [3,3]
function [ T, R ] = solvesvd( B, NN )
num = length(B);
%1.Seeking centroid
cen_B = sum(B)/num;
cen_NN = sum(NN)/num;
%2.Decentralization:Set centroids as reference origin for both clusters
B2 = B-repmat(cen_B,num,1);
NN2 = NN-repmat(cen_NN,num,1);
%3.svd decompose:[U,S,V] = svd(A) ==> A = U*S*V'
H = B2'*NN2;
[U,~,V] = svd(H);
R = V*diag([1 1 sign(det(V*U'))])*U';
T = cen_NN' - R*cen_B';
T = T';
end
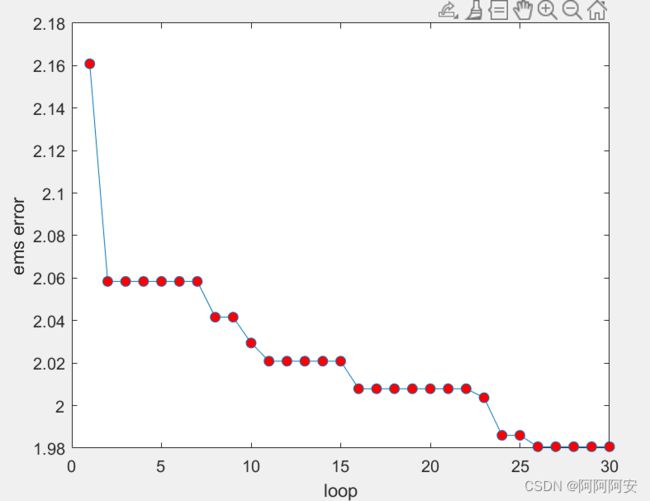
三.实现效果
注意:上图中蓝色为初始稀疏点云,黑色为配准后的稀疏点云结果