【RL】6.Actor-Critic

RL-Ch6-Actor-Critic

A2C：Advantage Actor-Critic

A3C：Asynchronous Actor-Critic

Advantage Function

我们在第四章Policy Gradient中从原始的梯度计算公式，引入baseline和时间步衰减的技巧后，得到Advantage Function，形式如下：
$$A^{\theta }(s_t,a_t)=\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n-b$$

令
$$G_t^n=\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n$$
则对$G_t^n$的估计可以用如下式子
$$G_t^n<--E[G_t^n]=Q^{\pi }(s_t,a_t)$$
而$b=V^{\pi }(s_t^n)$，所以Advantage Function的新形式为
$$A^{\theta }(s_t,a_t)=Q^{\pi }(s_t,a_t)-V^{\pi }(s_t^n)$$

需要估计两个Network，但我们可以采用只估计一个Network的方法。

由于
$$Q^{\pi }(s_t,a_t)=E[r_t^n+V^{\pi }(s_{t+1}^n)]$$

不考虑随机性，去掉期望号，则有
$$Q^{\pi }(s_t,a_t)=r_t^n+V^{\pi }(s_{t+1}^n)$$

最终Advantage Function的形式为
$$A^{\theta }(s_t,a_t)=r_t^n+V^{\pi }(s_{t+1}^n)-V^{\pi }(s_t^n)$$

估计$r_t^n$的方差比$G_t^n$的小，因为只需要估计一个状态s。

Advantage Actor-Critic

概念

A2C相比Q-Learning，把基于Q值变为基于V值为导向，而且策略更新的方法引入了Policy Gradient的方法。

技巧

1. actor$\pi (s)$与critic$V^{\pi }(s)$的一些参数可以共享。

2. 探索很重要，如果交叉熵更大，则$\pi (s)$的分布更均匀。

Asynchronous Advantage Actor-Critic

Asynchronous

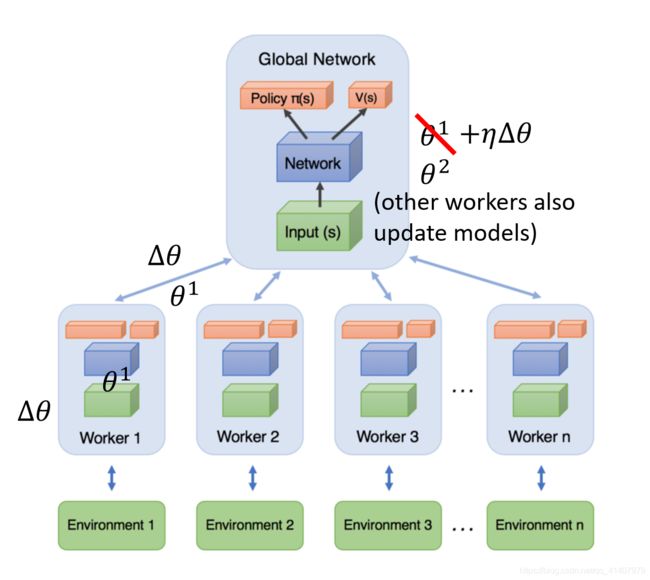
基本想法是开多个worker，进行经验的集成。具体实现步骤为：

1. 每个worker从云端下载全局参数到本地端
2. 每个worker分别在本地端采样
3. 每个worker在本地端计算梯度
4. 将梯度上传云端更新全局参数

不是同步更新，而是一个worker计算完就上传更新全局参数，像一个自助售卖机一样，谁有需求就去买饮料，交易一次云端就处理一次。

Pathwise Derivative Policy Gradient

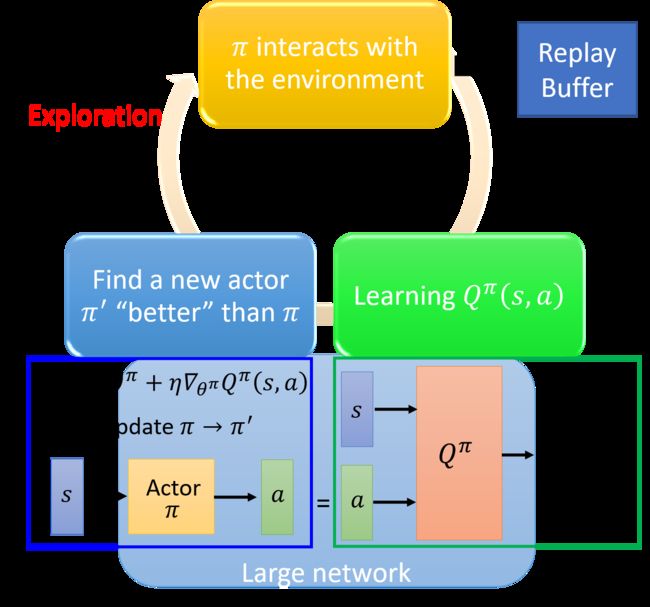
PDPG是解决Q-Learning无法解决连续动作空间问题的一个方法，同时也是一个特别的Actor-Critic方法：原始的AC是只告知什么是不好的，而改进后的AC会告知什么是不好的，还会指导下一步应该怎么做。

此时动作a是一个连续的数值，要解决$a=arg{\max }_{a}Q(s,a)$，这个问题的解决要看Actor$\pi$。问题的求解流程图如下：

我们在第五章提到过Q-Learning算法，而不同点就在于如下五点：

•Initialize Q-function Q, target Q-function $\hat{Q}=Q$, actor $\pi$, target actor $\hat{\pi }=\pi$

•In each episode

​ •For each time step t

​ •Given state $s_t$, take action $a_t$ based on Q $\pi$(epsilon greedy exploration)

​ •Obtain reward $r_t,$ and reach new state $s_{t+1}$

​ •Store $(s_t,a_t,r_t,s_{t+1})$ into buffer

​ •Sample $(s_i,a_i,r_i,s_{i+1})$ from buffer (usually a batch)

​ •Target $y=r_i+$\max_a⁡[\hat{Q}(s_{i+1},a)]​$Q(s_{t+1},\hat{\pi }(s_{t+1}))$

​ •Update the parameters of Q to make $Q(s_i,a_i)$ close to y (regression)

​ •Update the parameters of $\pi$ to maximize $Q(s_i,\pi (s_i))$

​ •Every C steps reset $\hat{Q}=Q$

​ •Every C steps reset $\hat{\pi }=\pi$

AC vs. GAN