模拟退火算法学习笔记
0 基本术语介绍
（1）组合优化（Combinatorial Optimization）
组合优化问题的目标是从组合问题的可行解集中求出最优解，通常可描述为：令Ω＝{S1，S2，…，Sn}为所有状态构成的解空间，C(Si)为状态Si对应的目标函数值，要求寻找最优解S*，使得对于所有的Si∈Ω，有C(S*)＝minC(Si)。
典型的组合优化问题有旅行商问题（Traveling Salesman Problem－TSP）、0-1背包问题（Knapsack Problem）等。
（2）蒙特卡罗方法(Monte Carlo Methods)
蒙特卡罗方法又叫统计模拟方法，它使用随机数（或伪随机数）来解决计算的问题，是一类重要的数值计算方法。该方法的名字来源于世界著名的赌城蒙特卡罗，而蒙特卡罗方法正是以概率为基础的方法。
一个使用蒙特卡罗方法的简单例子：假设需要计算一个不规则图形的面积，首先把图形放到一个已知面积的方框内，然后朝在方框内均匀地撒豆子，之后再数这个图形之中有多少颗豆子，再根据图形内外豆子的比例来计算面积。当豆子越小，撒得豆子数量越多的时候，结果就越精确。
（3）模拟退火之加热过程（熔解）
增强粒子运动，消除系统原先可能存在的非均匀态。
（4）模拟退火之等温过程
对于与环境换热而温度不变的封闭系统，系统状态的自发变化总是朝自由能减少的方向进行，当自由能达到最小时，系统达到平衡。
（5）模拟退火之冷却过程
使粒子热运动减弱并渐趋有序，系统能量逐渐下降，从而得到低能的晶体结构。
（6）Metropolis 采样之接受准则
固体在恒定温度下达到热平衡的过程可以用 Metropolis 方法加以模拟。温度恒定时：若在温度T时，对于当前状态i和新状态j，若Ej小于Ei，则接受j为当前状态；否则需要考察其接受概率若概率
大于[0,1)区间的随机数，则仍接受状态j为当前状态；若不成立则保留状态i为当前状态。在高温下，可接受与当前内能差较大的新状态；在低温下，只接受与当前状态能量差较小的新状态。
（7）Metropolis采样之稳定准则
判断固体在恒定温度下是否达到热平衡的准则可以采用Metropolis采样稳定准则，该准则主要可采取检验目标函数的均值是否稳定；连续若干步的目标值变化较小以及按一定的步数抽样等方式判断是否达到热平衡。此外，一般采用按照一定步数采样即可。
（8）鲁棒性
鲁棒是Robust的音译，也就是健壮和强壮的意思。所谓鲁棒性，是指控制系统在一定（结构，大小）的参数摄动下，维持其它某些性能的特性。
1 模拟退火简介
模拟退火算法 (Simulated Annealing Algorithm，SAA) 最早的思想是由 Metropolis 等人于1953年提出，但提出后似乎没有引起太大反响。直到1983年, Kirkpatrick 等人成功地将退火思想引入到组合优化领域之后，该算法便逐渐被广泛应用于各大领域。
SAA是一种通用的优化方法，是局部搜索方法的扩展。不同于局部搜索算法的地方是以SAA一定的概率选择邻域中目标值大的劣质解。SAA目前广泛应用于生产调度、控制工程、机器学习、神经网络、模式识别、图像处理、离散/连续变量的结构优化问题等领域。
SAA具有十分强大的全局搜索性能。SAA中基本不用搜索空间的知识或者其他的辅助信息，而只是定义邻域结构，在其邻域结构内选取相邻解，再结合目标函数与Metropolis采样接受准则以评估是否采纳新解；模拟退火算法不是采用确定性规则，而是采用概率的变迁来指导它的搜索方向（状态转移函数是依据概率分布设置的），它所采用的概率仅仅是作为一种工具来引导其搜索过程朝着更优化解的区域移动。因此，虽然它看起来是一种盲目的搜索方法，但实际上有着明确的搜索方向。
2 模拟退火理论
2.1 实际退火过程
退火过程：将物体加热到足够高的温度后逐渐熔解为液体；在高温下，液体的大量分子彼此之间进行着相对自由移动；如果该液体冷却速度足够慢，那么在每个温度下的液体粒子都可以达到一个平衡态，最后形成一个纯净的晶体。这中缓慢冷却的过程就是退火过程。对于这个物体来说，晶体状态是能量最低状态，而所有缓慢冷却的系统都可以自然达到这个最低能量状态。实际上，如果液态物体被迅速冷却，那么它不会达到这一能量最低的晶体状态，而是只能达到一种具有较高能量的多晶体状态或非结晶状态（此快速冷却过程被称为淬火）。简单而言，物理退火过程由以下几部分组成：加温过程、等温过程和冷却过程。
2.2 模拟退火过程
SSA的退火过程是基于Monte Carlo迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表控制，包括控制参数的初值T0及其衰减因子k、每个T值时的迭代次数L（此即为Metropolis采样稳定准则）和停止条件。
模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却。加温时，固体内部粒子随温升变为无序状，内能增大；而徐徐冷却时粒子渐趋有序，在每个温度上都达到平衡态，最后在常温时达到基态，内能减为最小。
模拟退火算法与金属退火过程的相似关系如表1所示。根据Metropolis准则，粒子在温度T时趋于平衡的概率为 ，其中E为温度T时的内能，
为其改变量。
用固体退火模拟组合优化问题，将内能E模拟为目标函数值，温度T演化成控制参数，即得到解组合优化问题的模拟退火算法：由初始解X1和控制参数T的初值T0开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，此迭代过程模拟的是在给定温度下物体达到热平衡的过程；在给定温度达到热平衡后，再逐步减小T值，重新进行热平衡迭代直到达到终止条件。算法终止时的当前解就是近似最优解。
表1物理退火与模拟退火的异同
| 物理退火 |
模拟退火 |
| 物体内部状态 |
解空间 |
| 状态对应的内能 |
目标函数值 |
| 温度 |
控制参数 |
| 熔解过程 |
设定初温 |
| 等温过程（状态转移） |
Metropolis采样过程 |
| 冷却过程 |
控制参数下降 |
| 能量最低态 |
最优解 |
2.3 模拟退火过程的算法思想
模拟退火的主要思想是：在搜索区间随机游走（即随机选择点），再利用Metropolis采样接受准则，使随机游走逐渐收敛于局部最优解。而温度是Metropolis算法中的一个重要控制参数，可以认为这个参数的大小控制了随机过程向局部或全局最优解移动的快慢。
Metropolis采样接受准则是一种有效的接受方法，其算法为：系统从一个能量状态变化到另一个状态时，相应的能量从E1变化到E2，其概率为：
(1)
如果E2<E1，系统接受此状态；否则以一个随机的概率接受或丢弃此状态。状态2被接受的概率为：
(2)
(3)
如果是求解最大值而不是最小值，需要将上式按照下面改写：
(4)
在使用Metropolis采样接受准则时，新状态下的能量如果减小，则直接接受其状态（局部最优）；否则则以一定概率接受。模拟退火算法从某个初始解出发，经过大量当前解的变换后，可以求得给定控制参数值时组合优化问题的相对最优解。然后减小控制参数T的值，重复执行Metropolis采样接受算法，就可以在控制参数T减小到一定数值时，最终求得组合优化问题的整体最优解。控制参数的值必须缓慢衰减，否则不能称之为退火过程，无法达到最低能量值。
2.4 模拟退火算法的特点
模拟退火算法求得的解与初始解状态（算法迭代的起点）无关，具有渐近收敛性，已在理论上被证明是一种以概率l收敛于全局最优解的优化算法。
模拟退火算法适用范围广，求得全局最优解的可靠性高；算法简单，便于实现；该算法的搜索策略有利于避免搜索过程因陷入局部最优解的缺陷，有利于提高求得全局最优解的可靠性；模拟退火算法还具有十分强的鲁棒性。具有这些特点的原因是比起普通的优化搜索方法而言，它采用了许多独特的方法和技术。其方法和技术主要有以下几个方面：
（1）以一定的概率接受恶化解
模拟退火算法在迭代过程中不仅接受使目标函数值变“好”的点，而且还能够以一定的概率接受使目标函数值变“差”的点。迭代过程中出现的状态是随机产生的，并且不强求后一状态一定优于前一状态，而且对于差解的接受概率随着温度的下降而逐渐减小。
很多传统的优化算法往往是确定性的，从一个搜索点到另一个搜索点的转移有确定的转移方法和转移关系，这种确定性往往可能使得搜索点远达不到最优点，从而陷入局部最优的困境。
（2）引进算法控制参数
引进退火温度作为算法控制参数，将优化过程分成熔解、等温和冷却三个阶段，并分别设定各个阶段下参数的取舍和变化规则。
模拟退火算法有三个重要的步骤：一是熔化过程，该过程需要设置控制参数的初始值；二是等温过程，该过程在每个控制参数下，由前迭代点出发，依据状态转移函数产生邻近的随机状态，由控制参数确定的Metropolis接受准则决定此新状态的取舍；三是冷却过程，该过程缓慢降低控制参数，提高接受准则，直至控制参数达到要求。控制参数的改变而造成的接受准则的提高是提高算法全局性能的关键。
（3）对目标函数要求少
传统搜索算法不仅需要利用目标函数值，而且往往需要目标函数的导数值等其他一些辅助信息才能确定搜索方向；当这些信息不存在时，算法就失效了。而模拟退火算法不需要其他的辅助信息，而只是定义邻域结构，在其邻域结构内选取相邻解，再用目标函数进行评估即可。
3 模拟退火算法改进
在确保一定要求的优化质量基础上，提高模拟退火算法的搜索效率，是对模拟退火算法改进的主要内容。
有如下可行的方案：
- 选择合适的初始状态；
- 设计合适的状态产生函数，使其根据搜索进程的需要表现出状态的全空间分散性或局部区域性；
- 设计高效的退火过程，改进对温度的控制方式；
- 采用并行搜索结构，设计合适的算法终止准则。
此外，对模拟退火算法的改进，也可通过增加某些环节来实现。主要的改进方式有：
- 增加记忆功能。为避免搜索过程中由于执行概率接受环节而遗失当前遇到的最优解，可通过增加存储环节，将到目前为止的最好状态存储下来；
- 增加升温或重升温过程。在算法进程的适当时机，将温度适当提高，从而可激活各状态的接受概率，以调整搜索进程中的当前状态，避免算法在局部极小解处停滞不前；
- 对每一当前状态，采用多次搜索策略，以概率接受区域内的最优状态，而不是标准模拟退火算法的单次比较方式；
- 与其他搜索机制的算法（如遗传算法、免疫算法等）相结合，可以综合其他算法的优点，提高运行效率和求解质量。
4 模拟退火算法流程
模拟退火算法可以分解为熔解过程、等温过程和冷却过程。熔解过程主要是初始化控制参数T0、获取初始解状态X1，每个T值的迭代次数L；等温过程主要是通过状态转移函数获取X2、使用Metropolis采样接受准则接受或者舍弃X2；冷却过程主要是使用温度冷却函数降低控制参数T。
该算法具体流程如下：
- 初始化：设置初始温度T0(充分大）、初始解状态X1(（是算法迭代的起点）、每个T值的迭代次数L（此为Metropolis采样稳定判断准则）；
- 对k=1，…，L做第(3)至第(6)步；
- 使用状态转移函数产生新解X2；
- 计算增量
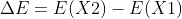，其中E(X)为评价函数; - 若
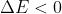，则接受X2作为新的当前解，否则以概率接受X2作为新的当前解（此为Metropolis采样稳定判断准则）； - 如果控制参数T满足终止条件，则输出当前解作为最优解，结束程序；
- 如果不满足终止条件，逐渐减小T转第(2)步。
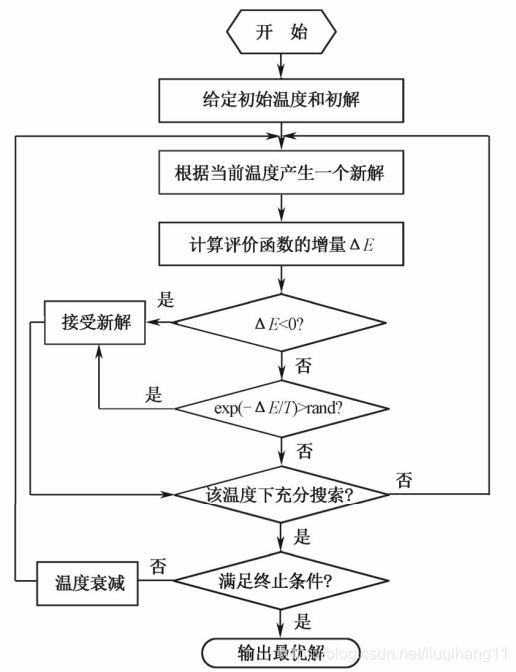
模拟退火的算法流程图如下：
|
|
| 图1模拟退火算法流程图 |
5 模拟退火算法基本要素说明
模拟退火算法的性能质量高，比较通用，而且容易实现。不过，为了得到最优解，该算法通常要求较高的初温以及足够多次的抽样，这使算法的优化时间往往过长。
从算法结构可知，新的状态产生函数、初温、状态转移函数、接受概率函数、退温函数、同温下的迭代次数和算法停止准则是直接影响算法优化结果的关键参数或关键函数。
5.1基本参数说明
5.1.1 初温
温度T在算法中具有决定性的作用，它直接控制着退火的走向。由随机移动的接受准则可知：初温越大，获得高质量解的几率就越大，且Metropolis的接收率越接近于1。然而，初温过高会使计算时间增加。因此，初温的确定应折中考虑优化质量和优化效率，确定初温的常用方法包括以下几种：
- 可以均匀抽样一组状态，以各状态目标值的方差为初温；
- 随机产生一组状态，确定两两状态间的最大目标值差
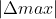，然后依据差值,利用一定的函数确定初温； - 利用经验公式给出初始温度。
一般而言，直接设定初温的值即可。
5.1.2 同温下的迭代次数
同温下的迭代次数L的选取原则是在衰减参数T的衰减函数已选定的前提下，L应选得在控制参数的每一取值上都能恢复准平衡，一般L取100～1000。
5.1.3 算法停止准则
算法停止准则用于决定算法何时结束。可以简单地设置温度终值Tend：当衰减温度T达到Tend时算法终止。然而，模拟火算法的收敛性理论中要求Tend趋向于零，这其实是不实际的。常用的停止准则包括：设置终止温度的阈值；设置迭代次数阈值；或者当搜索到的最优值连续保持不变时停止搜索。
5.2 基本函数说明
5.2.1 状态转移函数
设计状态转移函数应该考虑到尽可能地保证所产生的候选解遍布全部解空间。候选解一般采用按照某一概率密度函数对解空间进行随机采样来获得。概率分布可以是均匀分布、正态分布、指数分布等。
5.2.2 退温函数
退温函数即温度更新函数，用于在外循环中修改温度值。目前，最常用的温度更新函数为指数退温函数。假设时刻k的温度用Tk来表示，时刻k+1的温度用Tk+1来表示，降温方式可表示为：
(5)
k越接近1温度下降越慢，且其大小可以不断变化，一般取0.98-0.9的范围。
5.2.3 接受概率
接受概率指从一个状态X1(一个可行解)向另一个状态X2(另一个可行解)的转移概率，通俗的理解是接受一个新解为当前解的概率。它与当前的控制参数T有关，随温度下降而减小。一般采用Metropolis准则，如前面的公式(1-3)所示。
6 代码展示
6.1 一个Python实现的模拟退火算法(函数最值问题)
代码来自 '模拟退火算法(1) - Python实现 - LOGAN_XIONG - 博客园 (cnblogs.com)'
import numpy as np
import matplotlib.pyplot as plt
import random
class SA(object):
def __init__(self, interval, tab='min', T_max=10000, T_min=1, iterMax=1000, rate=0.95):
self.interval = interval # 给定状态空间 - 即待求解空间
self.T_max = T_max # 初始退火温度 - 温度上限
self.T_min = T_min # 截止退火温度 - 温度下限
self.iterMax = iterMax # 定温内部迭代次数
self.rate = rate # 退火降温速度
#############################################################
self.x_seed = random.uniform(interval[0], interval[1]) # 解空间内的种子
self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值；'max' - 最大值
#############################################################
self.solve() # 完成主体的求解过程
self.display() # 数据可视化展示
def solve(self):
temp = 'deal_' + self.tab # 采用反射方法提取对应的函数
if hasattr(self, temp):
deal = getattr(self, temp)
else:
exit('>>>tab标签传参有误："min"|"max"<<<')
x1 = self.x_seed
T = self.T_max
while T >= self.T_min:
for i in range(self.iterMax):
f1 = self.func(x1)
delta_x = random.random() * 2 - 1
if x1 + delta_x >= self.interval[0] and x1 + delta_x <= self.interval[1]: # 将随机解束缚在给定状态空间内
x2 = x1 + delta_x
else:
x2 = x1 - delta_x
f2 = self.func(x2)
delta_f = f2 - f1
x1 = deal(x1, x2, delta_f, T)
T *= self.rate
self.x_solu = x1 # 提取最终退火解
def func(self, x): # 状态产生函数 - 即待求解函数
value = np.sin(x**2) * (x**2 - 5*x)
return value
def p_min(self, delta, T): # 计算最小值时，容忍解的状态迁移概率
probability = np.exp(-delta/T)
return probability
def p_max(self, delta, T):
probability = np.exp(delta/T) # 计算最大值时，容忍解的状态迁移概率
return probability
def deal_min(self, x1, x2, delta, T):
if delta < 0: # 更优解
return x2
else: # 容忍解
P = self.p_min(delta, T)
if P > random.random(): return x2
else: return x1
def deal_max(self, x1, x2, delta, T):
if delta > 0: # 更优解
return x2
else: # 容忍解
P = self.p_max(delta, T)
if P > random.random(): return x2
else: return x1
def display(self):
print('seed: {}\nsolution: {}'.format(self.x_seed, self.x_solu))
plt.figure(figsize=(6, 4))
x = np.linspace(self.interval[0], self.interval[1], 300)
y = self.func(x)
plt.plot(x, y, 'g-', label='function')
plt.plot(self.x_seed, self.func(self.x_seed), 'bo', label='seed')
plt.plot(self.x_solu, self.func(self.x_solu), 'r*', label='solution')
plt.title('solution = {}'.format(self.x_solu))
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.savefig('SA.png', dpi=500)
plt.show()
plt.close()
if __name__ == '__main__':
SA([-5, 5], 'max')6.2 一个MATLAB实现的模拟退火算法(TSP问题)
代码来自《智能优化算法及其MATLAB实例（第2版）》第七章的实例7.3
%%%%%%%%%%%%%%%%%%%%%%模拟退火算法解决TSP问题%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
C=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
3238 1229;4196 1044;4312 790;4386 570;3007 1970;2562 1756;...
2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;...
3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
2370 2975]; %31个省会城市坐标
n=size(C,1); %TSP问题的规模,即城市数目
T=100*n; %初始温度
L=100; %马可夫链长度
K=0.99; %衰减参数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%城市坐标结构体%%%%%%%%%%%%%%%%%%%%%%%%%%
city=struct([]);
for i=1:n
city(i).x=C(i,1);
city(i).y=C(i,2);
end
l=1; %统计迭代次数
len(l)=func3(city,n); %每次迭代后的路线长度
figure(1);
while T>0.001 %停止迭代温度
%%%%%%%%%%%%%%%%多次迭代扰动，温度降低之前多次实验%%%%%%%%%%%%%%%
for i=1:L
%%%%%%%%%%%%%%%%%%%计算原路线总距离%%%%%%%%%%%%%%%%%%%%%%%%%
len1=func3(city,n);
%%%%%%%%%%%%%%%%%%%%%%%%%产生随机扰动%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%随机置换两个不同的城市的坐标%%%%%%%%%%%%%%%%%
p1=floor(1+n*rand());
p2=floor(1+n*rand());
while p1==p2
p1=floor(1+n*rand());
p2=floor(1+n*rand());
end
tmp_city=city;
tmp=tmp_city(p1);
tmp_city(p1)=tmp_city(p2);
tmp_city(p2)=tmp;
%%%%%%%%%%%%%%%%%%%%%%%%计算新路线总距离%%%%%%%%%%%%%%%%%%%%
len2=func3(tmp_city,n);
%%%%%%%%%%%%%%%%%%新老距离的差值，相当于能量%%%%%%%%%%%%%%%%%
delta_e=len2-len1;
%%%%%%%%%%%%新路线好于旧路线，用新路线代替旧路线%%%%%%%%%%%%%%
if delta_e<0
city=tmp_city;
else
%%%%%%%%%%%%%%%%%%以概率选择是否接受新解%%%%%%%%%%%%%%%%%
if exp(-delta_e/T)>rand()
city=tmp_city;
end
end
end
l=l+1;
%%%%%%%%%%%%%%%%%%%%%%%%%计算新路线距离%%%%%%%%%%%%%%%%%%%%%%%%%%
len(l)=func3(city,n);
%%%%%%%%%%%%%%%%%%%%%%%%%%%温度不断下降%%%%%%%%%%%%%%%%%%%%%%%%%%
T=T*K;
for i=1:n-1
plot([city(i).x,city(i+1).x],[city(i).y,city(i+1).y],'bo-');
hold on;
end
plot([city(n).x,city(1).x],[city(n).y,city(1).y],'ro-');
title(['优化最短距离:',num2str(len(l))]);
hold off;
pause(0.005);
end
figure(2);
plot(len)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')7 参考资料
[1] 智能优化算法及其MATLAB实例（第2版），包子阳等.
链接: https://pan.baidu.com/s/1hXGvsEJfP4nBFpkaQ-zxIA 提取码: j9qb
[2] 模拟退火算法(1) - Python实现 - LOGAN_XIONG - 博客园 (cnblogs.com).
[3] 模拟退火算法详解 - 百度文库 (baidu.com).
[4] 计算智能，张军等.
链接: https://pan.baidu.com/s/1ahstyLP-vP7Y_r0gbbQx0A 提取码: nf3t