Canny边缘检测方法中的非极大抑制

什么是非极大抑制

在目标检测中，通常会使用各种各样的方法来让计算机找到目标的所在位置，然而，计算机的输出往往并不是单一的，也就是说，一个目标可能会输出多个结果（如下图所示），这些结果有好有坏，因此就需要使用非极大抑制的方法来筛选出最优结果，说白了也就是一个剔除冗余的过程。

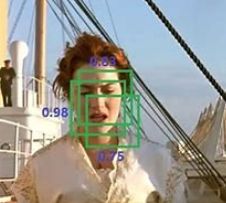
非极大值抑制（Non-Maximum Suppress，NMS）算法，其核心思想在于抑制非极大值的目标（去冗余），从而搜索出局部极大值的目标（找最优）。由于不同的目标框有不同的表示方式，因此NMS算法也具有不同的变体，本文通过目标检测的非极大抑制引入，简单讲述非极大抑制的思想以及其在边缘检测上的应用。

目标检测中的非极大抑制算法实现

（1）假设有n个候选预测框，将所有可能的预测框按类别划分n个集合，把整张图片也加入到集合当中，使得集合中存在n+1个元素
（2）用置信度最高的元素分别与其余元素之间计算IoU，如果IoU大于给定阈值，则将置信度较低的元素排除，保留置信度较高的元素。
IoU是两个区域重叠的部分除以两个区域的集合部分得出的结果，通过设定的阈值，与这个IoU计算结果比较。这里借用网络上的一张图片来帮助大家理解

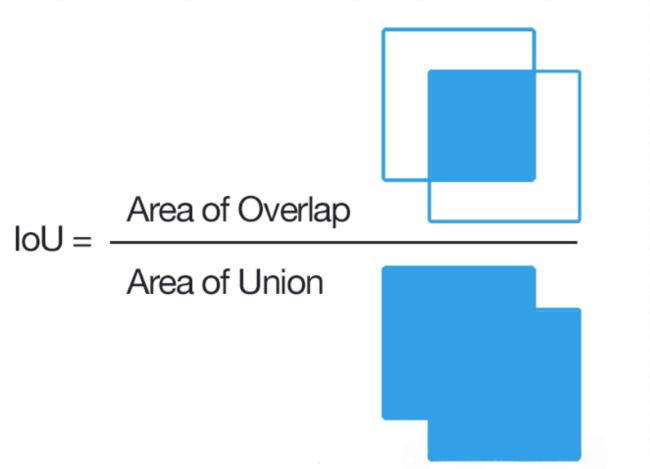
（3）重复上述步骤，直到找出最优解为止。

非极大抑制在边缘检测中有什么作用

利用sobel算子可以计算图像梯度的幅值和方向，Sobel算子分为X方向和Y方向，表达如下
S x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] S_x = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix} Sx​= ​−1−2−1​000​121​ ​
S y = [ − 1 − 2 − 1 0 0 0 1 2 1 ] S_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix} Sy​= ​−101​−202​−101​ ​
直接利用两个边缘检测卷积核，分别对图像进行边缘提取后再叠加，即可初步得到边缘图像。使用改算子进行卷积前，需要先将图像转化为单通道的灰度图。MATLAB代码如下：

conv1 = [1 0 -1 
         2 0 -2 
         1 0 -1]; 
  
conv2 = [1 2 1 
         0 0 0 
        -1 -2 -1]; 
         
% 也可以直接写成表达式 
% 其中I为目标图像对应的二值图像 
R=zeros(m,n); 
for xi=2:1:m-1 
    for yi = 2:1:n-1 
        R(xi,yi)=abs(I(xi+1,yi+1)+2*I(xi,yi+1)+I(xi-1,yi+1)-I(xi-1,yi-1)-2*I(xi,yi-1)-I(xi+1,yi-1))+abs(I(xi-1,yi-1)+2*I(xi-1,yi)+I(xi-1,yi+1)-I(xi+1,yi+1)-2*I(xi+1,yi)-I(xi+1,yi-1)); 
    end 
end 

做完这一步后，我们会发现，检测出来的边缘像素点有许多冗余，也就是同一个边缘可能检测了两条、三条甚至更多条。因此，我们就需要使用非极大抑制的方法来消除冗余，此处可参考J.Canny发表的论文

梯度方向上的非极大抑制

接下来进入本文的正题，
在John Canny提出的Canny算子的论文中，非最大值抑制就只是在0、90、45、135四个梯度方向上进行的，每个像素点梯度方向按照相近程度用这四个方向来代替。这四种情况也代表着四种不同的梯度，即
$G_y>G_x$，且两者同号
$G_y>G_x$，且两者异号
$G_y<G_x$，且两者同号
$G_y<G_x$，且两者异号

如上图所示，根据X方向和Y方向梯度的大小可以判断A点是靠近X轴还是Y轴，通过A1和A2的像素值则可计算A点的亚像素值，B点同理，不再赘述。上面两图为靠近Y轴的梯度大，下面两图为靠近X轴的像素大。
由于A、B两点的位置是通过梯度来确定的，那么A、B两点的梯度值也可以根据Q点的梯度计算，因此假设Q点在四个方向上的梯度分别为$G_1、G_2、G_3、G_4$。下面我们分情况来讨论

1. 首先讨论$G_y>G_x$的情况，此时

$$w=\frac{G_x}{G_y}$$
$$G_2=G(i-1,j)$$
$$G_4=G(i+1,j)$$
如果两者同号，则
$$G_1=G(i-1,i-1)$$
$$G_3=G(i+1,i+1)$$
否则
$$G_1=G(i-1,i+1)$$
$$G_3=G(i+1,i-1)$$

2. 然后是$G_y<G_x$的情况

$$w=\frac{G_y}{G_x}$$
$$G_2=G(i,j-1)$$
$$G_4=G(i,j+1)$$
如果两者同号
$$G_1=G(i+1,i-1)$$
$$G_3=G(i-1,i+1)$$
否则
$$G_1=G(i-1,i-1)$$
$$G_3=G(i+1,i+1)$$
如此便可以计算出两个相邻亚像素点的梯度值
$$g_A=w\ast G_1+(1-w)\ast G_2$$
$$g_B=w\ast G_3+(1-w)\ast G_4$$
比较三者的像素值，如果Q点像素值大于其余两者，则保留Q点作为边缘上的点，否则认为Q点为冗余点。

参考链接

(36条消息) 非极大值抑制算法详解_武乐乐~的博客-CSDN博客_非极大值抑制算法
(36条消息) Canny算子中的非极大值抑制（Non-Maximum Suppression）分析_Belial_2010的博客-CSDN博客_canny算子非极大值抑制
(36条消息) Canny边缘检测Step3——梯度幅值的非极大值抑制（NMS）详解_Polaris_T的博客-CSDN博客_canny 非极大值抑制