长短期记忆(LSTM)相关知识
文章目录
- LSTM结构
-
- 遗忘门
- 输入门
-
- 决定给细胞状态C添加哪些新的信息
- 更新旧的细胞信息
- 输出门
- LSTM小结
-
- 如何实现长期依赖?
- 如何避免梯度消失/爆炸?
- 双向LSTM(Bi-LSTM)
- GRU
上一篇文章中,提到RNN难以学习到长期依赖关系,后来有人提出了RNN的改进版本LSTM很大程度上改善了长期依赖问题。
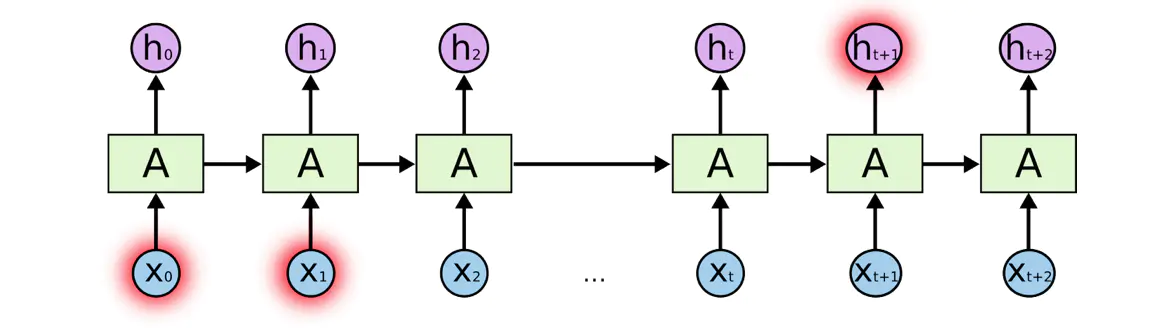
长期依赖在序列数据中是很常见的,考虑到下面这句话“I grew up in France… I speak fluent French.”,现在需要语言模型通过现有以前的文字信息预测该句话的最后一个词,模型结构的可能如下图所示:
需要通过以前文字语境来预测出最后一个词是French,则需要依赖于开头部分语境中的单词France。LSTM可以很容易的学习到这种长期依赖,这得益于其内部三个特殊的门结构。
LSTM结构
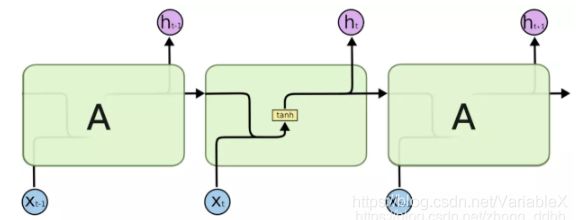
RNN结构如下图所示:
LSTM基于RNN,做出了些调整,修改后的结构如图所示:
很明显可以看到两个区别,一方面是细胞单元内部的结构变复杂了,另一方面相邻细胞单元之间的依赖关系从一个变为了两个。
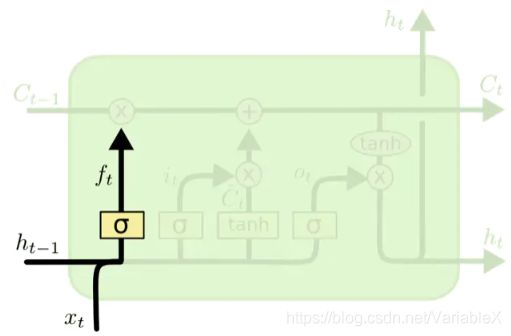
具体来说,LSTM使用上图中三个黄色σ方框(σ代表Sigmoid运算)代表的遗忘门、输入门和输出门来控制细胞状态。
遗忘门
遗忘门控制前一步记忆单元中的信息以多大程度被遗忘掉,主要决定决定细胞状态 C 需要丢弃哪些信息。遗忘门在细胞单元中的位置,如下图黄色方框所示:
其中遗忘门的输出结果 f f f的计算公式为:
f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_t=\sigma(W_f\cdot[h_{t-1},\;x_t]+b_f) ft=σ(Wf⋅[ht−1,xt]+bf)
式子中: W f W_f Wf是遗忘门的权重矩阵, [ h t − 1 , x t ] [h_{t-1},\;x_t] [ht−1,xt]表示把两个向量连接成一个更长的向量, b f b_f bf是遗忘门的偏置项, σ \sigma σ 表示Sigmoid函数,最终得到一个介于0与1之间的输出值。
其中 W f ⋅ [ h t − 1 , x t ] + b f W_f\cdot[h_{t-1},\;x_t]+b_f Wf⋅[ht−1,xt]+bf 可以理解为:
[ W f ] [ h t − 1 x t ] = [ W f h W f x ] [ h t − 1 x t ] = W f h h t − 1 + W f x x t \begin{aligned} \begin{bmatrix}W_f\end{bmatrix}\begin{bmatrix}\mathbf{}h_{t-1}\\ \mathbf{}x_t\end{bmatrix}&= \begin{bmatrix}W_{fh}&W_{fx}\end{bmatrix}\begin{bmatrix}\mathbf{}h_{t-1}\\ \mathbf{}x_t\end{bmatrix}\\ &=W_{fh}\mathbf{}h_{t-1}+W_{fx}\mathbf{}x_t \end{aligned} [Wf][ht−1xt]=[WfhWfx][ht−1xt]=Wfhht−1+Wfxxt
也就是遗忘门通过查看 h ( t − 1 ) h_{(t-1)} h(t−1)和 x t x_t xt的信息计算得到一个介于0与1之间的向量,该向量中的数值决定从上一个单元输入到此单元的状态 C t − 1 C_{t-1} Ct−1 中有多少信息需要保留或丢弃,0表示不保留,1表示都保留。至于这个细胞状态 C t − 1 C_{t-1} Ct−1代表什么,后面会有相关的解释说明。
输入门
决定给细胞状态C添加哪些新的信息
接下来是决定给细胞状态C添加哪些新的信息。这一步又分为两个步骤:
1,首先,利用 h t − 1 h_{t-1} ht−1和 x t x_t xt通过输入门的运算来决定更新哪些信息,输入门的位置如下图中的黄色σ方框所示:
输入门的运算如下:
i t = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) \mathbf{}i_t=\sigma(W_i\cdot[\mathbf{}h_{t-1},\mathbf{x}_t]+\mathbf{}b_i) it=σ(Wi⋅[ht−1,xt]+bi)
2,然后,利用 h t − 1 h_{t-1} ht−1和 x t x_t xt通过一个tanh层得到新的候选细胞信息 C ~ t \tilde{C}_t C~t,这些信息可能会被更新到细胞信息中,涉及的运算如下:
C ~ t = tanh ( W c ⋅ [ h t − 1 , x t ] + b c ) \tilde{C}_t=\tanh(W_c\cdot[\mathbf{}h_{t-1},\mathbf{}x_t]+\mathbf{}b_c) C~t=tanh(Wc⋅[ht−1,xt]+bc)
更新旧的细胞信息
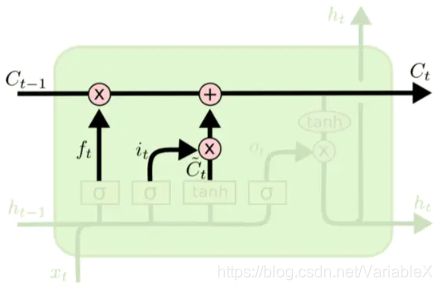
通过上面的两个步骤,得到了新的信息,接下来就是更新旧的细胞信息,变为新的细胞信息。更新的规则就是通过遗忘门的选择来忘记旧细胞信息的一部分,通过输入门的选择来添加候选细胞信息 C ~ t \tilde{C}_t C~t的一部分得到新的细胞信息。如下图所示:
相关的计算如下:
C t = f t ∗ C t − 1 + i t ∗ C ~ t \mathbf{}C_t=f_t*{\mathbf{}C_{t-1}}+i_t*{\mathbf{}\tilde{C}_t} Ct=ft∗Ct−1+it∗C~t
通过这样的方式,我们就把LSTM关于当前的记忆 C ~ t \tilde{C}_t C~t和长期的记忆 C t − 1 C_{t-1} Ct−1组合在一起,形成了新的单元状态。由于遗忘门的控制,它可以保存很久很久之前的信息,由于输入门的控制,它又可以避免当前无关紧要的内容加入记忆。
输出门
更新完细胞状态后需要根据输入的 h t − 1 h_{t-1} ht−1和 x t x_t xt来决定输出细胞状态C的哪些特征,这里需要将输入经过一个称为输出门的Sigmoid函数,其位置如下图黄色方框所示:
经过Sigmoid表示的门之后,还需要经过一个tanh函数来得到取值范围在 -1~1 之间的向量,该向量与输出门得到的输出结果相乘就得到了最终该RNN单元的输出 h t h_t ht。涉及的计算如下:
o t = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) h t = o t ∗ tanh ( c t ) \mathbf{}o_t=\sigma(W_o\cdot[\mathbf{}h_{t-1},\mathbf{}x_t]+\mathbf{}b_o) \\ \mathbf{}h_t=\mathbf{}o_t* \tanh(\mathbf{}c_t) ot=σ(Wo⋅[ht−1,xt]+bo)ht=ot∗tanh(ct)
LSTM小结
如何实现长期依赖?
当输入序列没有重要信息时,LSTM遗忘门的值接近为1,输入门接近0,此时过去的记忆会被保存,从而实现了长期记忆;
当输入的序列中出现了重要信息时,LSTM会将其存入记忆中,此时输入门的值会接近于1;
当输入序列出现重要信息,且该信息意味着之前的记忆不再重要的时候,输入门接近1,遗忘门接近0,这样旧的记忆被遗忘,新的重要信息被记忆。
经过这样的设计,整个网络更容易学习到序列之间的长期依赖。
如何避免梯度消失/爆炸?
在LSTM中,状态 C 是通过累加的方式来计算的,不像RNN中的累乘的形式,这样的话,它的的导数也不是乘积的形式,这样就不会发生梯度消失的情况了。
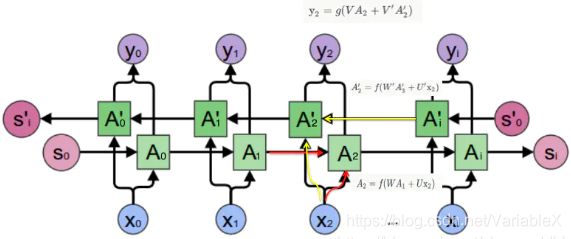
双向LSTM(Bi-LSTM)
上面介绍的是单向的LSTM,只能根据先前的序列推导未来的信息,但是有时候在给定时间 t 之后的未来的信息,可以帮助推断时刻 t 的信息。例如在语言识别中,当前识别到的字可能取决于未来的几个字的发音。因此,在某些任务中,双向的 LSTM 要比单向的 LSTM 的表现要好。
双向LSTM(Bi-LSTM)的隐藏层要保存两个值, A 参与正向计算, A’ 参与反向计算。最终的输出值 y 取决于 A 和 A’,网络结构如下图所示:
以 t = 2 t=2 t=2为例,输入 x 2 x_2 x2, A 2 A_2 A2是正向计算的结果, A ’ 2 A’_2 A’2是反向计算的结果,输出 y 2 y_2 y2同时取决于 A 2 , A ’ 2 A_2,A’_2 A2,A’2。
GRU
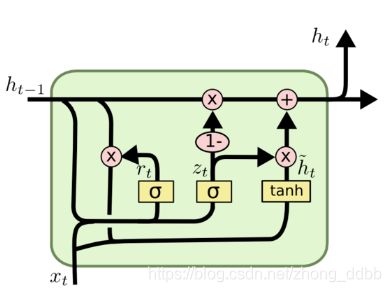
GRU(Gated Recurrent Unit)作为LSTM的一种变体,与LSTM有两个不同点:
(1)GRU将LSTM中的两个信息流简化成一个信息流,输入只有一个 h t \boldsymbol h_t ht。
(2)GRU将遗忘门和输入门合成了一个单一的更新门,还引入了一个重置门。
如下图所示:
主要运算过程如下:
r t = σ ( W r ⋅ [ h t − 1 , x t ] ) z t = σ ( W z ⋅ [ h t − 1 , x t ] ) h ~ t = tanh ( W ⋅ [ r t ∗ h t − 1 , x t ] ) h t = ( 1 − z t ) ∗ h t − 1 + z t ∗ h ~ t \begin{aligned} &r_t = \sigma(W_r\cdot[h_{t-1},x_t]) \\ &z_t = \sigma(W_z\cdot[h_{t-1},x_t]) \\ &\tilde h_t = \tanh(W \cdot[r_t * h_{t-1},x_t]) \\ & h_t = (1-z_t)*h_{t-1} + z_t*\tilde h_t \end{aligned} rt=σ(Wr⋅[ht−1,xt])zt=σ(Wz⋅[ht−1,xt])h~t=tanh(W⋅[rt∗ht−1,xt])ht=(1−zt)∗ht−1+zt∗h~t
相当于简化了LSTM,运算速度提高了很多,并且应用效果也没有差很多。
参考文章:
-
LSTM原理详解
-
理解LSTM(通俗易懂版)
-
NLP面试题目汇总1-5