天池工业蒸汽量预测-模型调参

本文改编自《阿里云天池大赛赛题解析-机器学习篇》工业蒸汽量预测的模型调参。进行了部分素材的替换和知识点的归纳总结。新增了Datawhale8月集成学习中的网格搜索、随机搜索的内容
上一篇工业蒸汽量预测-模型验证

5.2 模型调参

5.2.1 调参

1.调参的目标

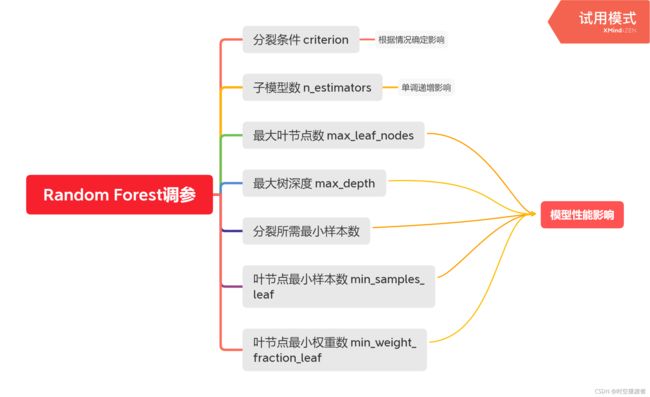
调参就是对模型的参数进行调整，以找到使模型性能最优的参数。调参的目标就是达到整体模型的偏差和方差的大和谐！参数可分为两类：过程影响类参数和子模型影响类参数。具体来说，过程影响类参数就是在子模型不变的前提下，调整“子模型数（n_estimators）”、“学习率（learning_rate）”等参数，改变训练过程，从而提高整体模型的性能。子模型影响类参数就是调整“最大树深度（max_depth）”、“分裂条件（criterion）”等参数，改变子模型的性能，从而提高整体模型的性能。bagging的训练过程旨在降低方差，而boosting的训练过程旨在降低偏差，过程影响类的参数能够引起整体模型性能的大幅度变化。

下面是Datawhale8月集成学习中关与参数分类的解释，分为参数和超参数两类。

2.参数对整体模型性能的影响

5.2.2 网格搜索

网格搜索（Grid Search）是一种穷举搜索的调参手段。在所有候选的参数选择中，通过循环遍历，尝试每一种可能性，表现最好的参数就是最终的结果。其原理就像是在数组中找最大值。以有两个参数的模型为例，参数a有三种可能，参数b有4种可能，把所有可能性列出来，可以表示成一个3*4的表格，其中每个单元就是一个网格，循环过程就像是在每个网格中遍历、搜索，因此得名网格搜索。

下面是一个简单的网格搜索示例，应用iris数据集，对SVC模型参数做一次网格搜索调参。

	C=0.001	C=0.01	…	C=10
grmma=0.001	SVC(C=0.001,grmma=0.001)	SVC(C=0.01,grmma=0.001)	…	SVC(C=10,grmma=0.001)
grmma=0.01	SVC(C=0.001,grmma=0.01)	SVC(C=0.01,grmma=0.01)	…	SVC(C=10,grmma=0.01)
…	…	…	…	…
grmma=100	SVC(C=0.001,grmma=100)	SVC(C=0.01,grmma=100)	…	SVC(C=10,grmma=100)

具体的代码和调参结果如下：

from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import numpy as np
iris = load_iris()
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=0)
print("Size if training set:{} size of testing size:{}".format(X_train.shape[0],X_test.shape[0]))  #total number 150

'''
C:正则化参数。正则化的强度与C成反比。必须严格为正。惩罚是平方的l2惩罚。
kernel:{'linear'，'poly'，'rbf'，'sigmoid'，'precomputed'}，默认='rbf'
degree:多项式和的阶数
gamma:“ rbf”，“ poly”和“ Sigmoid”的内核系数。
shrinking:是否软间隔分类，默认true
'''

# grid search start
best_score = 0 
for gamma in [0.001,0.01,0.1,1,10,100]:
    for C in [0.001,0.01,0.1,1,10,100]:
        svm = SVC(gamma=gamma,C=C) #对于每种参数的可能组合，都进行一次训练
        svm.fit(X_train,y_train)
        score = svm.score(X_test,y_test)
        if score > best_score:
            best_score = score
            best_parameters = {'gamma':gamma,'C':C}
# grid search end
print("Best score:{:.2f}".format(best_score))
print("Best parameters:{}".format(best_parameters))

网格搜索GridSearchCV()：
网格搜索结合管道：

5.2.3 随机搜索

网格搜索相当于暴力地从参数空间中每个都尝试一遍，然后选择最优的那组参数，这样的方法显然是不够高效的，因为随着参数类别个数的增加，需要尝试的次数呈指数级增长。有没有一种更加高效的调优方式呢？那就是使用随机搜索的方式，这种方式不仅仅高效，而且实验证明，随机搜索法结果比稀疏化网格法稍好(有时候也会极差，需要权衡)。参数的随机搜索中的每个参数都是从可能的参数值的分布中采样的。与网格搜索相比，这有两个主要优点：

• 可以独立于参数数量和可能的值来选择计算成本。
• 添加不影响性能的参数不会降低效率。

5.2.4 调参实例

# 我们先来对未调参的SVR进行评价： 
from sklearn.svm import SVR     # 引入SVR类
from sklearn.pipeline import make_pipeline   # 引入管道简化学习流程
from sklearn.preprocessing import StandardScaler # 由于SVR基于距离计算，引入对数据进行标准化的类
from sklearn.model_selection import GridSearchCV  # 引入网格搜索调优
from sklearn.model_selection import cross_val_score # 引入K折交叉验证
from sklearn import datasets

boston = datasets.load_boston()     # 返回一个类似于字典的类
X = boston.data
y = boston.target
features = boston.feature_names
pipe_SVR = make_pipeline(StandardScaler(),SVR())
score1 = cross_val_score(estimator=pipe_SVR,X = X,y = y,scoring = 'r2',cv = 10)       # 10折交叉验证
print("CV accuracy: %.3f +/- %.3f" % ((np.mean(score1)),np.std(score1)))

CV accuracy: 0.187 +/- 0.649

交叉验证经常与网格搜索进行结合，作为参数评价的一种方法，这种方法叫做grid search with cross validation。sklearn因此设计了一个这样的类GridSearchCV，这个类实现了fit，predict，score等方法，被当做了一个estimator，使用fit方法，该过程中：（1）搜索到最佳参数；（2）实例化了一个最佳参数的estimator；

# 下面我们使用网格搜索来对SVR调参：
from sklearn.pipeline import Pipeline
pipe_svr = Pipeline([("StandardScaler",StandardScaler()),
                                                         ("svr",SVR())])
param_range = [0.0001,0.001,0.01,0.1,1.0,10.0,100.0,1000.0]
param_grid = [{"svr__C":param_range,"svr__kernel":["linear"]},  # 注意__是指两个下划线，一个下划线会报错的
                            {"svr__C":param_range,"svr__gamma":param_range,"svr__kernel":["rbf"]}]
gs = GridSearchCV(estimator=pipe_svr,param_grid = param_grid,scoring = 'r2',cv = 10)       # 10折交叉验证
gs = gs.fit(X,y)
print("网格搜索最优得分：",gs.best_score_)
print("网格搜索最优参数组合：\n",gs.best_params_)

网格搜索最优得分： 0.6081303070817127
网格搜索最优参数组合：
{‘svr__C’: 1000.0, ‘svr__gamma’: 0.001, ‘svr__kernel’: ‘rbf’}

# 下面我们使用随机搜索来对SVR调参：
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import uniform  # 引入均匀分布设置参数
pipe_svr = Pipeline([("StandardScaler",StandardScaler()),
                                                         ("svr",SVR())])
distributions = dict(svr__C=uniform(loc=1.0, scale=4),    # 构建连续参数的分布
                     svr__kernel=["linear","rbf"],                                   # 离散参数的集合
                    svr__gamma=uniform(loc=0, scale=4))

rs = RandomizedSearchCV(estimator=pipe_svr,
                                                     param_distributions = distributions,
                                                     scoring = 'r2',
                                                      cv = 10)       # 10折交叉验证
rs = rs.fit(X,y)
print("随机搜索最优得分：",rs.best_score_)
print("随机搜索最优参数组合：\n",rs.best_params_)

随机搜索最优得分： 0.2994218818987872
随机搜索最优参数组合：
{‘svr__C’: 1.5375043685974368, ‘svr__gamma’: 0.9460163780038635, ‘svr__kernel’: ‘linear’}

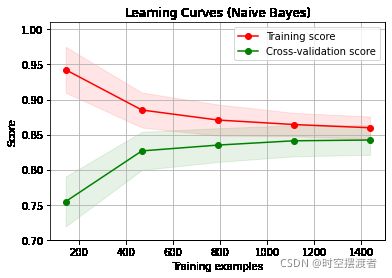
5.2.5 学习曲线

学习曲线是在训练集大小不同时，通过绘制模型训练集和交叉验证集上的准确率来观察模型在新数据上的表现，进而判断模型的方差或偏差是否过高，以及增大训练集是否可以减小过拟合。

5.2.6 验证曲线

和学习曲线不同，验证曲线的横轴为某一个超参数的一系列值，由此比较不同参数设置下（而非不同训练集大小）模型的准确率。

有关学习曲线和验证曲线的画法请参照参考资料中的链接。

参考资料

阿里云天池大赛赛题解析-机器学习篇