2022航电Navigable Proximity Graph-Driven Native Hybrid Queries with Structured and Unstructured

2022航电Navigable Proximity Graph-Driven Native Hybrid Queries with Structured and Unstructured Constraints

具有结构化和非结构化约束的可导航邻近图驱动原生混合查询

基本概念介绍

非结构化数据（如视频、文本、图像），通过特征向量准确地描述非结构化数据，通过向量相似度搜索来处理非结构化数据。

非结构化查询约束作为查询对象的特征向量（如论文）提供，

而结构化查询约束作为一组感兴趣的属性（如主题、地点和论文的发布年份）给出。（标签）（属性过滤）

hybrid query混合查询，它识别与查询对象具有相似特征向量的对象，并满足给定的属性查询约束。

动机

现存混合查询的解决方法

1. Vearch（京东）该策略很容易扩展到其他专用的向量相似度搜索库，如SPTAG，NGT，Faiss。
2. 阿里的ADBV，基于乘积量化（PQ）添加了多个查询计划。
3. Milvus：按照 访问频繁程度 划分子集，这样可以更快的搜索到符合查询的子集。然后对子集进行向量相似度搜索。

现存方法的局限

1. 必须同时维护两个索引。（属性索引、向量索引）（这不仅增加了内存开销，而且它还引入了额外的逻辑和一个后处理步骤 即合并，以确保两个索引的一致性和查询结果的正确性）
2. 由两种独立的修剪策略造成的不必要的计算开销。
3. 查询结果依赖于从两个子查询系统中获得的候选项的合并。（最后结果往往是少于K个的）
4. 现有的解决方案对PGs(邻近图)并不友好。first attribute filtering, then vector similarity search。由于许多研究表明，对于向量相似度搜索，PG比PQ快10倍，因此有必要利用一种方法将PG集成到混合查询方法中。

上述大多数限制是因为现有的解决方案致力于回答“分解-组装”decomposition-assembly模型中的混合查询，其中混合查询被分解为两个独立的子查询系统，这些系统分别处理，然后组装最终结果。

这促使我们提出了一个新的针对混合查询的通用框架，适合现有的pg，提供了设计良好的复合索引和联合修剪模块，以支持非结构化和结构化的查询约束，而不是同时维护两个独立的索引和分别执行修剪操作。

解决方案和贡献

解决方案

1. 框架首先将特征向量和属性嵌入到一个精心设计良好的复合索引中；
2. 然后通过考虑给定的非结构化和结构化查询约束来联合修剪复合索引上的搜索空间；
3. 它直接获得最终的top-k结果，而不是求助于合并操作。
4. NHQ是一个通用框架，其中复合索引是基于PG构建的，因此现有的PG很容易部署到NHQ，它还支持自定义优化的PG。

（对应局限的四点）

主要贡献

1. 我们提出了NHQ，一个通用的框架，用于以融合的方式回答具有非结构化和结构化约束的混合查询。我们的NHQ对现有的流行pg很友好，我们可以通过在NHQ中部署轻量级修改，为它们提供处理混合查询的强大能力。
2. 通过设计新的边缘选择和路由策略，我们提出了两种NPGs，与现有的PG相比，这两种策略在效率、准确性和内存使用方面具有更好的性能。
3. 我们在NHQ框架中部署了两个npg，从而获得了两种新的混合查询方法，它们在所有数据集上都显著优于最先进的竞争对手（在相同的召回下速度快10×）。
4. 我们在9个真实数据集上通过各种指标验证了该方法的有效性和效率的优势，并分别与6种流行的PGs和六种混合查询方法进行了比较。

Implementation Strategies实现策略

属性过滤比向量相似度搜索具有更高的单位效率

策略A：“首先是属性过滤，然后是向量相似度搜索。” 不同属性过滤后得到的向量集是动态的，不能实现构造向量索引。

策略B：“首先是向量相似度搜索，然后是属性过滤。”

1. 在完成向量相似度搜索后进行属性过滤。
2. 在向量相似度搜索的每一步之后进行属性过滤（检查所探索的每个对象的属性）。

如果最终我们需要返回k个最近邻，通常需要向量相似度搜索返回 超过k个 候选对象以进行后续的属性过滤。

策略C：“联合属性过滤和向量相似度搜索”。该策略对包含特征向量和属性信息的复合索引，同时进行向量相似度搜索和属性过滤。

给定一个查询对象和一个复合索引，我们在查询处理过程中联合修剪具有不同向量和不匹配属性的无希望对象，以便在没有中间候选对象的情况下 一步返回查询结果。

NATIVE HYBRID QUERY FRAMEWORK

现有的PG只包含特征向量的邻域关系，而排除了属性，因此不能直接用于构建复合索引。

基于特征向量和属性构建一个新的PG作为复合索引。

NHQ Framework

给定特征向量的距离和属性的距离，将它们融合成一个统一的距离是计算对象距离的基本前提

Fusion distance

属性向量之间的距离：

m是l(e)的维数

融合距离：

v(e)：特征向量

l(e)：属性向量

Optimal weight confifiguration最佳权重配置

m是属性向量的维数

不需要专门为不同的数据集配置它们。

基本思想：通过利用属性距离对特征向量的距离进行微调，得到了一个融合距离。（加权距离）

构建混合索引：

联合修剪

NPG

选边

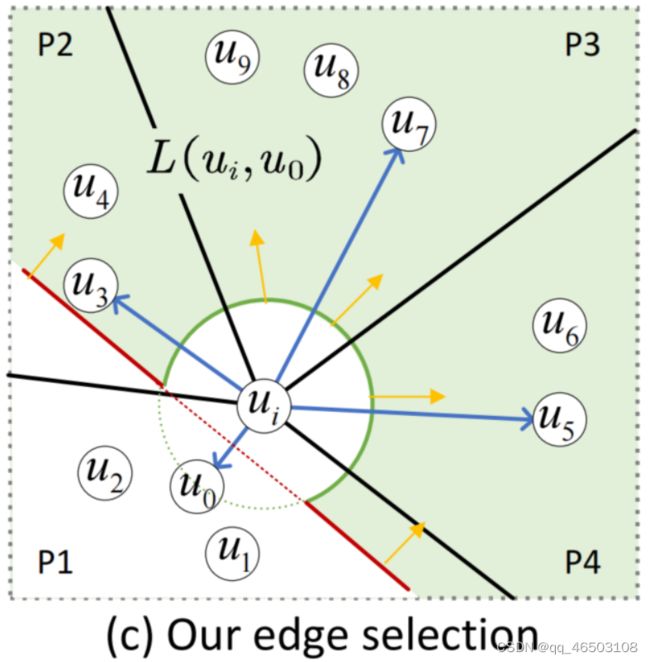
首先给出了由ui和ui的一个邻居uj∈N(ui)形成的 landing zone 的定义，它描述了只有其中的顶点可以添加到N(ui)中的区域。然后，我们给出了在landing zone外工作的边缘选择策略。

landing zone L(ui , uj ) =H(ui,uj ) \ B(ui, δ(ν(ui), ν(uj) ) )

连接ui和uj的直线的垂直平面U(ui,uj)（如图，红线） 将整个空间 分离成两个空间，H(ui,uj)为包含ui的半空间（如图的右上部分）。

B(ui, δ(ν(ui), ν(uj) ) ) 是以ui为球心，以 δ(ν(ui), ν(uj) ) 为半径的球体。

L(ui,uj)就是如图的绿色区域。

选边策略：

N(ui)中所有点和ui的landing zone的交集。这个交集中如果没有点，则选择该交集中距离ui最近的点添加到N(ui)中。

选边步骤：

1. 候选集初始化：C(ui)是V{ui}的子集，大小是l（l>=k，k是邻居集的上界）(随机选/通过额外的索引)
2. 邻居集初始化：根据到ui的距离升序排序C(ui)中的点，将最近的添加到N(ui)中，并且将该点在C(ui)中删除。
3. 邻居更新：我们从C(ui)中去除ui最近的顶点，加到N(ui)，iff up位于ui及其N(ui)中所有点形成的landing zone的新交叉区域

重复3直到候选集为空。

Routing

TOGG：

两个阶段

S1远离查询对象的阶段

S2更接近查询对象的阶段

在S1中，应该快速定位查询对象的邻域（用于效率要求），而在S2中，我们应该专注于全面访问离查询对象最近的顶点（用于准确性要求）。

TOGG使用树索引组织每个顶点的邻居。

我们的路由：

S1：设计了随机的TOGG，随机的选择ui的 k/h个邻居（1<=h<=k,k是顶点度的上界），计算距离。

S2：计算所有邻居和q的距离（贪婪）

NPG的结合

NPG_nsw,NPG_kgraph

NPG_nsw：

1. 候选集C(ui)的选择：NPG nsw是通过增量地插入一个对象来构造的。具体来说，一个新插入的对象ei∈S（对应于一个顶点ui）被视为查询对象，因此我们进行贪婪搜索，从插入的NPG nsw中获得l个最接近ui的顶点作为ui的候选邻居C（ui）
2. 邻居集N(ui)的选择：我们的选边。

NPG_kgraph：

1. 候选集C(ui)的选择：首先随机选择l个作为C(ui)，然后更新C(ui)，将更近的点更新进来。
2. 邻居集N(ui)的选择：我们的选边。

基于NPG的混合查询方法

NHQ_NPG_nsw,NHQ_NPG_kgraph

修改了npg的构建过程，将其原始的欧氏距离度量更改为我们的融合距离。

在S1中，我们的搜索只访问搜索路径中每个顶点的k/h个邻居，以提高效率（因此，我们修改了Alg.2的第5行（联合剪枝）随机访问每个顶点的 k/h邻居，并在第2-8行执行循环，直到它达到局部最优）

在S2中，我们设置了C = C∪R，并继续执行第2-8行（不修改第5行），全面访问搜索路径中顶点的所有邻居。最后，将R作为查询结果返回。