【读论文】1.0 TransE模型

Translating Embeddings for Modeling Multi-relational Data（2013/NIPS）

Abstract

•问题：把多关系数据的实体和关系嵌入到低维向量空间中

•多元关系数据：有向图中包括头实体h、尾实体t以及两者之间的关系r，表示为三元组(h,r,t)

•提出TransE：对向量空间中的三元组(h,r,t)进行操作，关系r视为翻译来进行建模的知识表示方法

 

简单来说，TransE就是讲知识图谱中的实体和关系看成两个Matrix。实体矩阵结构为 (ne* d)，其中ne表示实体数量，d表示每个实体向量的维度，矩阵中的每一行代表了一个实体的词向量；而关系矩阵结构为(nr*d)，其中nr代表关系数量，d表示每个关系向量的维度。TransE训练后模型的理想状态是，从实体矩阵和关系矩阵中各自抽取一个向量，进行L1或者L2运算，得到的结果近似于实体矩阵中的另一个实体的向量，从而达到通过词向量表示知识图谱中已存在的三元组的关系。

Translation-based model

在知识图谱的实体向量集中，随机取得头实体向量或尾实体向量并对初始三元组的对应向量进行替换，得到若干三元组d(h'+l,t')，构成训练集进行训练。

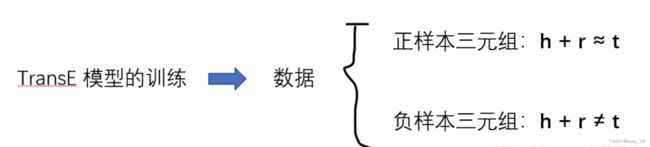 为了训练实体对嵌入和关系嵌入，需要引入负样本。 （正样本：翻译关系成立得到三元组，负样本：随机替换KG中现有的三元组中的头实体向量或尾实体向量构建的样本视为错误的样本， 这些错误的样本在这些三元组样本中，部分样本的翻译关系是不成立的）（负采样的过程也会无意构成正样本三元组，训练时影响最终的真实模型精度，因此在测试中也应该过滤掉，文中称为Filter）

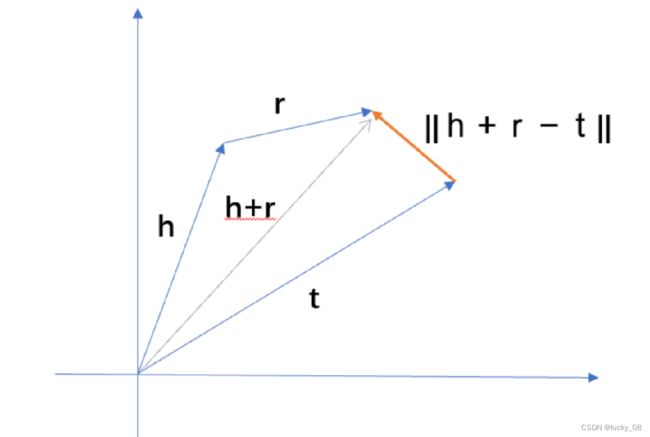
d ( h + r，t ) = || h + r - t ||，距离公式 d ( h + r，t ) 可以取 L1 或 L2 范数。我们可以看到正样本三元组距离函数值几乎为 0，负样本三元组的距离函数值较大，经过 L1 或 L2正则化确定最终的得分函数值，正则化后的值最终用于损失函数（这样可以避免训练出现过拟合），通过梯度下降朝着损失函数最小的方向更新参数，直至模型收敛，从而达到理想的精度。

 

  损失函数：

[]+=max{0,x} S'表示负样本的集合 margin γ 的作用相当于是一个正确triple与错误triple之前的间隔修正，margin越大，则两个triple之前被修正的间隔就越大，则对于词向量的修正就越严格。

d正三元组-d负三元组这个负数会越来越小，当这个负数的绝对值超过margin的时候，整个式子会变成负数，但是这个式子只取正数，当得到负数的时候就将整个式子置为0，所以正负三元组最大的距离就是margin,有了margin就不会让负样本的d是无限大的

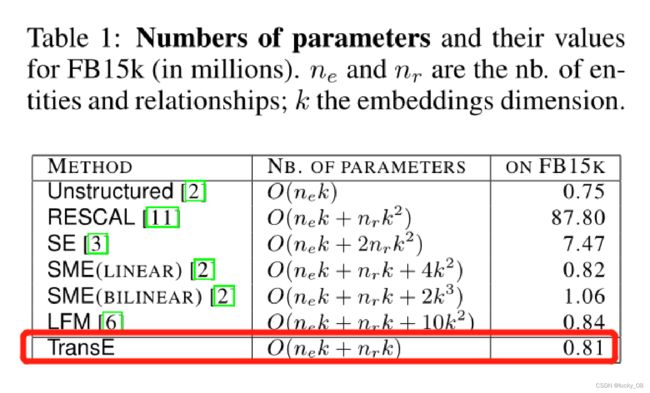
第3章表一提到了参数的总量为 O(nek+nrk) ，也就是说Loss更新的参数，是所有entities和relations的Embedding数据，设一共有 |E| 个实体和 |R| 个关系，每个实体/关系的向量长度为d维，因此，一共有（ |E| + |R| ） * d 个参数。

Loss function 希望达到的理想情况是，正确的triple的d(h + r , t) 尽可能的小，而错误triple的 d(h′+r,t′) 尽可能大，这样才能让总体的loss趋向于0。

算法流程如下：

 input: 输入模型的参数是训练集的三元组，实体集E，关系集L，margin，向量的维度k 1：对关系嵌入l进行·随机初始化 2：这里进行了L2范数归一化，也就是除以自身的L2范数 3：同理，也对实体进行了随机初始化， 4：训练的循环过程中： 5：首先对实体进行了L2范数归一化 6：取一个batch的样本，这里Sbatch代表的是正样本，也就是正确的三元组 7： 初始化三元组对，应该就是创造一个用于储存的列表 8，9，10：是根据Sbatch的正样本替换头实体或者尾实体构造负样本，然后把对应的正样本三元组和负样本三元组放到一起，组成Tbatch 11：完成正负样本的提取 12：根据梯度下降更新向量 13：结束循环

Experiments

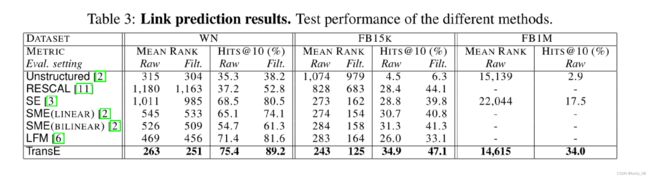
 在测试过程中，对于一个三元组，我们将头实体或尾实体替换成任意一种其他的实体，得到（n-1）个新的关系三元组，然后对这些三元组计算实体关系距离，将这n-1个三元组按照距离从小到大排列。看真实的三元组能排到多少。作者使用了两种评估方式：

meanrank：在测试集里，求真实的实体在n-1个元素中的排名，得出平均到第多少个才能匹配到正确的结果。

• Mean Rank: 正确结果排名之和/总查询次数；

• Hit@10: 排名在前10中正确的三元组所占的比例；

 作者又把所有关系分为一对一、一对多、多对一、多对多四大类，分别统计Hit@10。 结果显示： • 多对一的关系在预测尾实体时性能最好，一对多的关系在预测头实体时性能最好；

• Unstructured模型只在一对一的情况下表现良好；

• SME模型在某些情况下性能比TransE更好，这是因为训练数据更多。

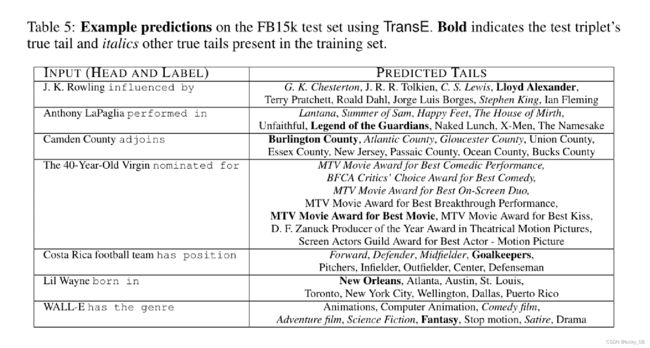
预测尾实体的例子：

 左边是输入头实体和关系向量【来自于知识图谱中对应的向量或矩阵表示】，右侧的尾实体向量是在训练集中按照排名规则，最有可能是真实的一些尾实体（Top 10）。加粗的尾实体是测试集中与头实体和关系向量真正对应或者真实的尾实体，由此可验证模型的质量如何。

 在少量样本中，给定头实体向量和关系，预测尾实体向量，左图表示测试集的平均排名情况（Loss），右图表示测试集Hits@top10中正确的比例(Accuracy)。可以发现当训练集越大，测试集中 TransE 的平均排名（或者说预测的平均损失值）下降的最快，右图表明，TransE模型的学习速度很快，在只有10个新关系的例子中，hits@10已经是达到约 18%，并且随着训练集中提供的样本数量的增加，效果改善明显。

Improvement

TransE优缺点：

优点：

① 解决多关系数据的处理问题，是一种简单高效的 KG 表示学习方法

② 能够完成多种关系的链接预测任务，能够自动且很好地捕捉推理特征

③ 适合在大规模复杂的 KG 上推广，是一种有效的 KG 推理手段

缺点：

• 表达能力不足，不能够有效充分的捕捉实体对间语义关系，无法有效处理一对多、多对一、多对多的关系以及自反关系。

• 处理图像信息效果差、负样本三元组的质量低、嵌入模型不能快速收敛、泛化能力差...

TransH：

 TransH解决上述TransE存在的问题 主要思路是因为实体在不同关系上有不同的embedding 主要操作方式是映射到超平面上

TransR：

 TransE和TransH算法存在的问题是: 实体和关系由于是不同类型的点，可能存在于不同的空间 TransR解决思路是将实体映射到关系的空间上，主要通过矩阵的转换映射

TransD：

 TransR存在的问题是：同一个关系对应的实体是同样的映射；映射只由关系决定；矩阵转换操作复杂度较大 TransD解决思路是: 将映射矩阵M用向量表示替代