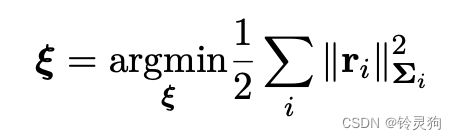【面试克星】【公式少代码少话多】Vins-Mono预积分相关知识点总结与概述

前言

Vins-Mono预积分相关的公式和代码可以在各个博客中找到。本文将充当一个帮助大家快速理解预积分、中值积分相关概述的角色，带大家理解代码，应对面试。

下面会分成三步，来帮助大家充分理解这个过程。步骤是按照顺序来写的。

中值积分和预积分

imu每进来一帧都会进行一步中值积分和预积分。

void push_back(double dt, const Eigen::Vector3d &acc, const Eigen::Vector3d &gyr)
{
    dt_buf.push_back(dt);
    acc_buf.push_back(acc);
    gyr_buf.push_back(gyr);
    propagate(dt, acc, gyr);
}

每进来一帧imu都会push_back一下，push_back内部调用了积分函数propagate
积分函数propagate中调用了midPointIntegration中值积分函数

midPointIntegration(_dt, acc_0, gyr_0, _acc_1, _gyr_1, delta_p, delta_q, delta_v,
                    linearized_ba, linearized_bg,
                    result_delta_p, result_delta_q, result_delta_v,
                    result_linearized_ba, result_linearized_bg, 1);

另外还有一个repropagate函数，作用：一个是初始化之后调用，重新积分。另一个是如果零偏更新幅度较大，则调用重新进行积分。这里不做过多讨论。

也就是传入了delta_t可以计算a、w的中值积分，将a、w的中值和之前的进行合并，就是预积分。

协方差和雅可比

在midPointIntegration函数中会对jacobian和convariance进行更新。

F.block<3, 3>(0, 0) = Matrix3d::Identity();
F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt + 
                     -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt * _dt;
F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt * _dt;
F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * -_dt;
F.block<3, 3>(3, 3) = Matrix3d::Identity() - R_w_x * _dt;
F.block<3, 3>(3, 12) = -1.0 * MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(6, 3) = -0.5 * delta_q.toRotationMatrix() * R_a_0_x * _dt + 
                     -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt;
F.block<3, 3>(6, 6) = Matrix3d::Identity();
F.block<3, 3>(6, 9) = -0.5 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt;
F.block<3, 3>(6, 12) = -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * -_dt;
F.block<3, 3>(9, 9) = Matrix3d::Identity();
F.block<3, 3>(12, 12) = Matrix3d::Identity();
//cout<<"A"<

MatrixXd V = MatrixXd::Zero(15,18);
V.block<3, 3>(0, 0) =  0.25 * delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 3) =  0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x  * _dt * _dt * 0.5 * _dt;
V.block<3, 3>(0, 6) =  0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 9) =  V.block<3, 3>(0, 3);
V.block<3, 3>(3, 3) =  0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(3, 9) =  0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(6, 0) =  0.5 * delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 3) =  0.5 * -result_delta_q.toRotationMatrix() * R_a_1_x  * _dt * 0.5 * _dt;
V.block<3, 3>(6, 6) =  0.5 * result_delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 9) =  V.block<3, 3>(6, 3);
V.block<3, 3>(9, 12) = MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(12, 15) = MatrixXd::Identity(3,3) * _dt;

//step_jacobian = F;
//step_V = V;
jacobian = F * jacobian;
covariance = F * covariance * F.transpose() + V * noise * V.transpose();

其中convariance的作用：

Jacobin的作用是在求残差之前使用这个jacobin对预积分值进行更新，更新后再求残差。

IMU残差

公式和细节代码在其他博客中都有介绍，这里只简要说明。

vins-mono中使用的是ceres::SizedCostFunction这个功能（是用ceres求残差的其中一种方法，不了解的话可以搜一搜）：

class IMUFactor : public ceres::SizedCostFunction<15, 7, 9, 7, 9>

自己的IMUFactor类继承ceres::SizedCostFunction这个类并重写其中的函数。
其中一个很重要的函数：Evaluate要被重写。
Evaluate中调用了：

residual = pre_integration->evaluate(Pi, Qi, Vi, Bai, Bgi,
                            Pj, Qj, Vj, Baj, Bgj);

对残差进行求解。