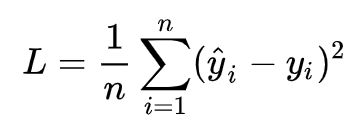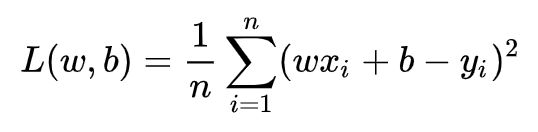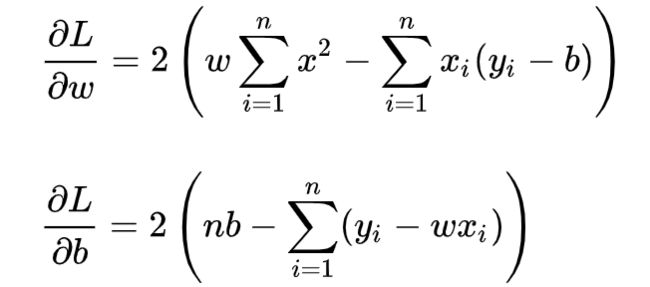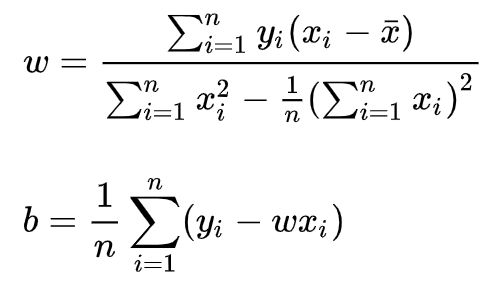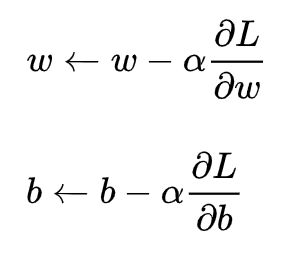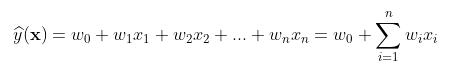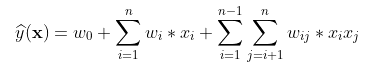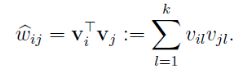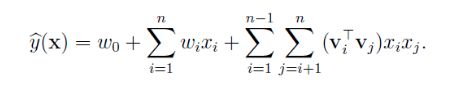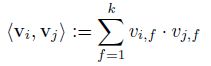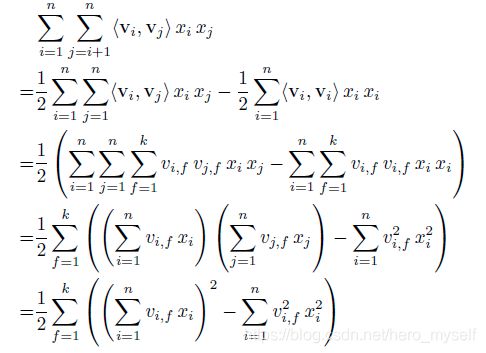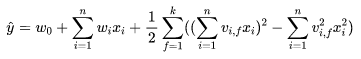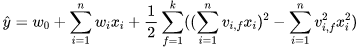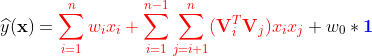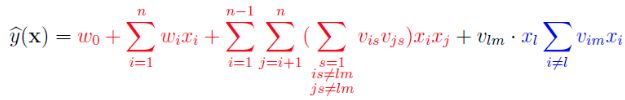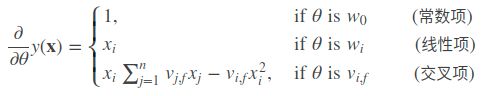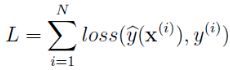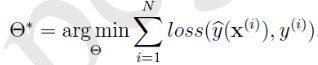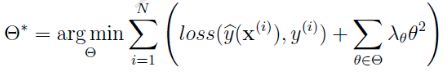【推荐算法】FM模型:Factorization Machines
1、线性回归
在介绍FM之前,我们先简单回顾以下线性回归。
回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析,时间序列模型以及发现变量之间的因果关系。通常使用曲线/直线来拟合数据点,目标是使曲线到数据点的距离差异最小。
线性回归是回归问题中的一种,线性回归假设目标值与特征之间线性相关,即满足一个多元一次方程。通过构建损失函数,来求解损失函数最小时的参数w和b。通常我们可以表达成如下公式:
![]() 为预测值,自变量x和因变量y是已知的,而我们想实现的是预测新增一个x,其对应的y是多少。因此,为了构建这个函数关系,目标是通过已知数据点,求解线性模型中w和b两个参数。
为预测值,自变量x和因变量y是已知的,而我们想实现的是预测新增一个x,其对应的y是多少。因此,为了构建这个函数关系,目标是通过已知数据点,求解线性模型中w和b两个参数。
求解最佳参数,需要一个标准来对结果进行衡量,为此我们需要定量化一个目标函数式,使得计算机可以在求解过程中不断地优化。针对任何模型求解问题,都是最终都是可以得到一组预测值![]() ,对比已有的真实值y,数据行数为n,可以将损失函数定义如下:
,对比已有的真实值y,数据行数为n,可以将损失函数定义如下:
即预测值与真实值之间的平均的平方距离,统计中一般称其为MAE(mean square error)均方误差。把之前的函数公式代入损失函数,并且将需要求解的参数w和b看做是函数L的自变量,可得:
现在的任务是求解最小化L时w和b的值,因此核心目标优化式转化为:
![]()
该问题的求解方式有两种:
- 最小二乘法(least square method)
求解w和b是使损失函数最小化的过程,在统计中,称为线性回归模型的最小二乘“参数估计”(parameter estimation)。我们可以将L(w,b)分别对w和b求导,得到:
令上述两式为0,可得到w和b最优解的闭式(closed-form)解:
- 梯度下降(gradient descent)
梯度下降核心内容是对自变量进行不断的更新(针对w和b求偏导),使得目标函数不断逼近最小值的过程:
这里多说一下线性回归与逻辑回归,逻辑回归是在线性回归的基础上多了一个sigmoid变换,具体的判别模型如下:
2、FM模型
FM算法是一种基于矩阵分解的机器学习算法,是为了解决大规模稀疏数据中的特征组合问题。
在传统的线性模型如LR中,每个特征都是独立的,如果需要考虑特征与特征之间的交互作用,可能需要人工对特征进行交叉组合;非线性SVM可以对特征进行kernel映射,但是在特征高度稀疏的情况下,并不能很好地进行学习;现在也有很多分解模型Factorization Model如矩阵分解MF、SVD++等,这些模型可以学习到特征之间的交互隐藏关系,但基本上每个模型都只适用于特定的输入和场景。
为此,在高度稀疏的数据场景下如推荐系统,FM(因子分解机)出现了。
FM考虑了特征之间的交互作用,并对特征进行了交叉组合。FM在线性模型的基础上添加了一个多项式,用于描述特征之间的二阶交叉(FM也支持多阶,本文以二阶FM为例)。
对于一个给定的特征向量![]() ,线性回归的模型函数为:
,线性回归的模型函数为:
其中,![]() 和
和![]() 为模型参数,特征分量
为模型参数,特征分量![]() 和
和![]() 之间是相互独立的,即
之间是相互独立的,即![]() 中仅考虑了单个的特征分量,而没有考虑特征分量之间的关系。为了表述特征之间的相互关系,在线性模型的基础上添加一个多项式,特征
中仅考虑了单个的特征分量,而没有考虑特征分量之间的关系。为了表述特征之间的相互关系,在线性模型的基础上添加一个多项式,特征![]() 和
和![]() 的组合用
的组合用![]() 表示,这里以二阶多项式模型为例,将
表示,这里以二阶多项式模型为例,将![]() 改写为:
改写为:
其中,n表示一个样本的特征的个数,两两交互可得到![]() 个交叉项,即
个交叉项,即![]() 种;
种;![]() 是特征组合对应的权重,用于表征这对特征组合的重要性,多项式要学习的参数即为n*(n-1)/2个w系数。
是特征组合对应的权重,用于表征这对特征组合的重要性,多项式要学习的参数即为n*(n-1)/2个w系数。
这种直接在![]() 前面配上一个系数
前面配上一个系数![]() 的方式在稀疏数据中有一个很大的缺陷,即参数
的方式在稀疏数据中有一个很大的缺陷,即参数![]() 学习困难,因为对
学习困难,因为对![]() 进行更新时,求得的梯度对应为
进行更新时,求得的梯度对应为![]() ,当且仅当
,当且仅当![]() 与
与![]() 都非0时参数才会得到更新。在高度稀疏的数据场景中,由于数据量不足,样本中出现未交互的特征分量是很普遍的,也就是说能够保证
都非0时参数才会得到更新。在高度稀疏的数据场景中,由于数据量不足,样本中出现未交互的特征分量是很普遍的,也就是说能够保证![]() 和
和![]() 都非0的组合较少,导致大部分参数
都非0的组合较少,导致大部分参数![]() 难以得到充分训练。
难以得到充分训练。
为了解决这个问题,FM算法对每个特征分量xi引入了一个k维(k<
![]() ,
, ![]() 。
。
FM对每个特征学习一个大小为k的一维向量,两个特征![]() 和
和![]() 的特征组合的权重值,可以通过特征对应的向量
的特征组合的权重值,可以通过特征对应的向量![]() 和
和![]() 的内积来表示。这样就可以利用向量内积
的内积来表示。这样就可以利用向量内积![]() 对
对![]() 求解:
求解:
于是,函数![]() 可以改写为(本文将下面的公式称为FM的计算公式):
可以改写为(本文将下面的公式称为FM的计算公式):
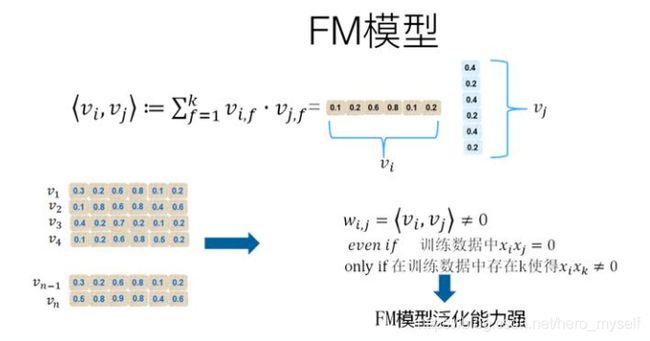
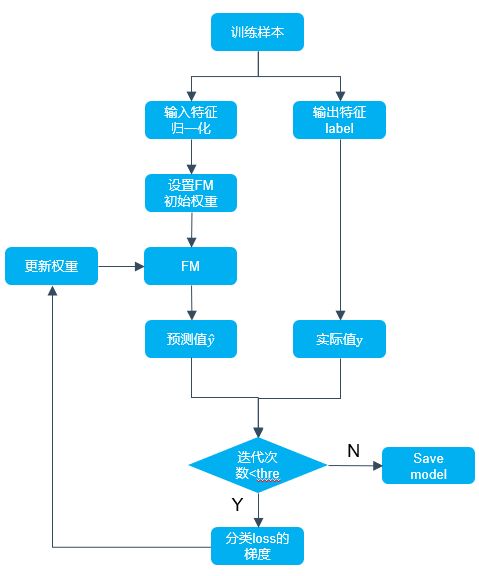
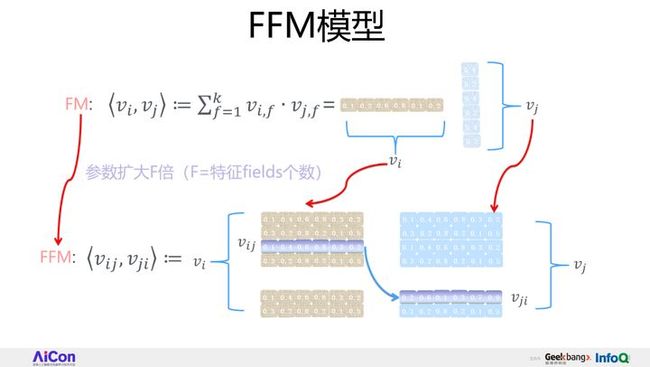
这样要学习的参数从 将vi按行拼成一个矩阵: 那么 这里简单解释下为什么FM的泛化能相比于SVM更强?参考下图进行说明:即使在训练数据里两个特征并未同时在训练实例里见到过,意味着 FM模型在做二阶特征组合的时候,对于每个二阶组合特征的权重,是根据对应两个特征的embedding向量内积,来作为这个组合特征重要性的指示。当训练好FM模型后,每个特征都可以学会一个特征embedding向量。 FM算法流程图(网上转载的一个Python版本的流程图): FM模型需要估计的参数包括: 直观上看FM的计算公式的计算复杂度为O(k*n^2): 通过数学公式的巧妙转化一下,就可以变成O(k*n)了。转化公式如下所示,其实就是利用了2xy = (x+y)^2 – x^2 – y^2的思路。 转换之后的FM计算公式可表示为: 转换之后的计算复杂度变为: 在高度稀疏的数据场景中,特征向量 这样,优化之后的FM模型为: 目前,FM的学习算法主要包括以下三种,本文只对随机梯度下降法进行简要介绍: 假设 对于任意的 在实际推导中,通常只计算 计算 由上式可知, FM的优化目标是整体损失函数: 对应不同的问题,比如分类、回归、排序等,这个loss函数通常有不同的选择方式,但这并不影响FM的最优化问题: 引入L2正则项,最优化问题变成,其中 SGD训练FM模型的算法流程: FM算法的优点: FM算法的缺点: FM与SVM的区别: FM和SVM的主要区别在于,SVM的二元特征交叉参数是独立的,如 为什么线性SVM在和多项式SVM在稀疏条件下效果会比较差呢?线性svm只有一维特征,不能挖掘深层次的组合特征在实际预测中并没有很好的表现;而多项式svn正如前面提到的,交叉的多个特征需要在训练集上共现才能被学习到,否则该对应的参数就为0,这样对于测试集上的case而言这样的特征就失去了意义,因此在稀疏条件下,SVM表现并不能让人满意。而FM不一样,通过向量化的交叉,可以学习到不同特征之间的交互,进行提取到更深层次的抽象意义。 此外,FM和SVM的区别还体现在: FFM的全称是Field-aware FM,直观翻译过来,就是能够意识到特征域(Field)的存在的FM模型。 FFM是FM的一个特例,它更细致地刻画了这个特征。首先它做了任意两个特征组合,但是区别在于,怎么刻划这个特征?FM只有一个向量,但FFM现在有两个向量,也就意味着同一个特征,要和不同的fields进行组合的时候,会用不同的embedding去组合,它的参数量更多。对于一个特征来说,原先是一个vector,现在会拓成F个vector,F是特征fields的个数,只要有跟其它特征的任意组合,就有一个vector来代表,这就是FFM的基本思想。 对于FFM的某个特征来说,会构造F个vector,来和任意其他的fields组合的时候,各自用各自的。假设模型具有n个特征,那么FM模型的参数量是n*k(暂时忽略掉一阶特征的参数),其中k是特征向量大小。而FFM模型的参数量呢?因为每个特征具有(F-1)个k维特征向量,所以它的模型参数量是(F-1)*n*k,也就是说参数量比FM模型扩充了(F-1)倍。FFM相对FM来说,参数量扩大了(F-1)倍,效果比FM好,但是要真的想把它用到现实场景中,存在着参数量太大这个问题。FFM中每个特征由FM模型的一个k维特征embedding,拓展成了(F-1)个k维特征embedding。之所以是F-1,而不是F,是因为特征不和自己组合。FM每个特征只有一个共享的embedding向量,而对于FFM的一个特征,则有(F-1)个特征embedding向量,用于和不同的特征域特征组合时使用。![]() 个
个![]() 系数变成了元素个数为n*k的V矩阵,因为k<
系数变成了元素个数为n*k的V矩阵,因为k<![]() 组成的交互矩阵可表示为
组成的交互矩阵可表示为![]() ,这个表达式对应了一种矩阵分解:
,这个表达式对应了一种矩阵分解:![]() 和
和![]() 一起出现的次数为0,如果换做SVM的模式,是无法学会这个特征组合的权重的。但是因为FM是学习单个特征的embedding,并不依赖某个特定的特征组合是否出现过,所以只要特征
一起出现的次数为0,如果换做SVM的模式,是无法学会这个特征组合的权重的。但是因为FM是学习单个特征的embedding,并不依赖某个特定的特征组合是否出现过,所以只要特征![]() 和其它任意特征组合出现过,那么就可以学习自己对应的embedding向量。于是,尽管
和其它任意特征组合出现过,那么就可以学习自己对应的embedding向量。于是,尽管![]() 和
和![]() 这个特征组合没有看到过,但是在预测的时候,如果看到这个新的特征组合,因为
这个特征组合没有看到过,但是在预测的时候,如果看到这个新的特征组合,因为![]() 和
和![]() 都能学到自己对应的embedding,所以可以通过内积计算出这个新特征组合的权重。这也是FM模型泛化能力强的根本原因。
都能学到自己对应的embedding,所以可以通过内积计算出这个新特征组合的权重。这也是FM模型泛化能力强的根本原因。
3、FM模型复杂度分析
![]() ,
,![]() ,
,![]() ,共有1+n+nk个模型参数,其中
,共有1+n+nk个模型参数,其中![]() 为整体的偏置量,
为整体的偏置量,![]() 为特征分量的各个分量的强度进行建模,
为特征分量的各个分量的强度进行建模,![]() 对特征向量中任意两个分量之间的关系进行建模。
对特征向量中任意两个分量之间的关系进行建模。![]() ,其中第一个花括号对应
,其中第一个花括号对应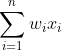 的加法和乘法操作数,第二个花括号对应
的加法和乘法操作数,第二个花括号对应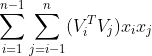 的加法和乘法操作数。
的加法和乘法操作数。![]() 。
。![]() 中绝大部分分量都为零,而转化后的计算公式关于i的求和只需在非0元素上进行,这样FM计算公式的复杂度就有O(k*n^2)变成了O(k*n),其中n是特征数量,k是特征的embedding size,这样就将FM模型改成了和LR类似和特征数量n成线性规模的时间复杂度了。
中绝大部分分量都为零,而转化后的计算公式关于i的求和只需在非0元素上进行,这样FM计算公式的复杂度就有O(k*n^2)变成了O(k*n),其中n是特征数量,k是特征的embedding size,这样就将FM模型改成了和LR类似和特征数量n成线性规模的时间复杂度了。
4、FM学习算法
![]() 表示FM的所有模型参数:
表示FM的所有模型参数:![]()
![]() ,存在两个与
,存在两个与![]() 的取值无关的函数
的取值无关的函数![]() 和
和![]() ,使得下面的等式成立:
,使得下面的等式成立:
![]() 时,
时,
![]() 时,
时,,
![]() 时,
时,![]() ,而
,而![]() 则利用
则利用![]() 来计算。
来计算。![]() 关于
关于![]() 的偏导数:
的偏导数:![]() 的训练只需要样本的
的训练只需要样本的![]() 特征非0即可,适合于稀疏数据。在使用SGD训练模型时,在每次迭代中,只需计算一次所有
特征非0即可,适合于稀疏数据。在使用SGD训练模型时,在每次迭代中,只需计算一次所有![]() 的
的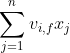 。
。![]() 表示参数
表示参数![]() 的正则化系数:
的正则化系数:
5、FM总结
![]() ,而FM的二元特征交叉参数是两个k维的向量vi、vj,这样子的话,
,而FM的二元特征交叉参数是两个k维的向量vi、vj,这样子的话,
6、FFM模型简介
![]()
7、参考博文