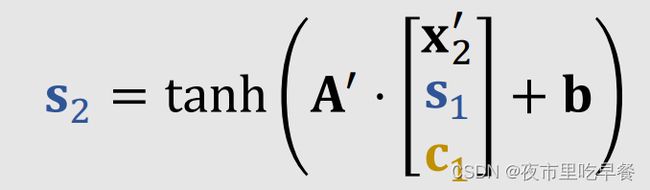RNN模型与NLP应用：Attention-8/9

目录

一、前言

二、attention改进seq2seq模型

三、总结

四、参考连接

---

一、前言

Seq2seq模型个别词语被忘记了，那么decode就无从得知完整的句子，也就不可能产生正确的翻译，如果你拿seq2seq做机器翻译，便会得到这样的结果。

横轴是句子的长度，纵轴机器翻译评估指标bleu，纵轴越高，说明机器翻译越准确，如果不用attention，输入句子超过20单词的时候，bleu便会下降，这是因为LSTM会遗忘，造成翻译出错，用attention得到红色曲线，这说明即使句子输入的很长，机器翻译的性能照样很好。

二、attention改进seq2seq模型

Attention是2015年论文提出的，用了attention，decoder每次更新状态的时候，都会再看一遍encoder所有状态，这样就不会遗忘，attention还可以告诉decoder应该关注encoder的哪个状态，这就是attention名字的由来，attention可以大幅提高准确率，但是attention缺点是计算量很大。

下面我们看attention的原理，在encoder已经结束工作之后，attention和decoder同时开始工作，回顾一下，decoder的初始状态s0是encoder最后一个状态hm，encoder的所有状态h1、h2、、、、hm都要保留下来，这里需要计算s0与每一个h的相关性，

下面我们具体来看一下，如何计算α

有很多种方法计算hi与s0的相关性，

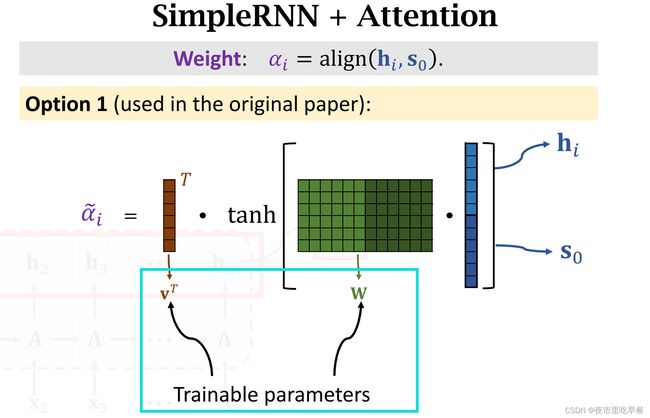
第一种：把hi与s0做concat，得到更高的向量，然后求矩阵w与这个向量的乘积，得到一个向量，再把双曲正切激活函数应用向量的每一个元素上，把每一个元素都压到-1——1之间，双曲正切函数的输出还是一个向量，最后计算向量v与刚算出来的向量的内积，两个向量的内积是个实数，记为，这里的

V和w都是参数，需要从训练数据中进行学习，算出这m个实数之后，对他们进行softmax变换，把输出结果记为α1到αm，由于α是softmax的输出，α1到αm都大于0，且相加等于1，这种计算权重α权重的方法，是attention第一篇论文提出的，在这之后，有很多论文提出其他计算权重的方法

以下这个计算权重α 的方法更加常用一些。

输入还是hi和s0这两个向量，第一步是分别用两个参数矩阵w和矩阵k，对这两个输入向量做线性变换，得到ki和q0，这两个参数矩阵需要从训练参数中进行学习，第二步是计算ki和 q0这两个向量的内积，把结果记为，由于m个k向量，所以得到m个，第三步是对从1到m进行softmax变换，把输出记作α1到αm，α1到αm都是整数，且相加等于1，这种计算权重的方法被transformer模型采用，

刚才讲的两种方法来计算hi和s0的相关性，随便用哪种方法都会得到m个α值，

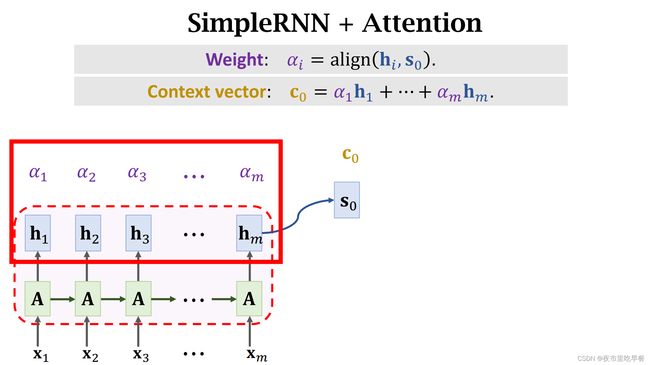
这些α被称为权重，每一个αi对应一个encoder状态hi，利用这些权重α，我们可以对这m个状态向量h求加权平均，计算α1*h1一直加到αm*hm，结果是个向量，记作c0，把c0称为Context vector，每一个Context vector c都会对应一个decoder s，Context vector c0对应decoder状态s0，decoder读入x1’，然后需要把状态更新为s1，具体该怎么样计算状态s1呢？

回归一下，假如不用attention，那么simpleRNN

是这样更新状态的，新的状态s1是新的输入x1’与旧的状态s0的函数，把x1’与s0做concat，然后乘到参数矩阵A’，加上向量b，再做双曲正切变换，得到新的状态s1，simpleRNN在更新状态只需要知道新的输入x1’，与旧的状态s0，simpleRNN并不去看encoder的状态，

用attention的话

更新decoder状态的时候，需要用到Context vector c0，把x1’,s0,c0一起做concat，用他们来计算新的状态s1，更新decoder状态s1，

回忆一下，c0是encoder所有状态h1到hm的加权平均，所以c0知道encoder的输入x1到xm的完整信息，decoder新的状态s1依赖context vector c0，这样一来，decoder也同样知道encoder完整的输入，于是RNN遗忘的问题便解决了

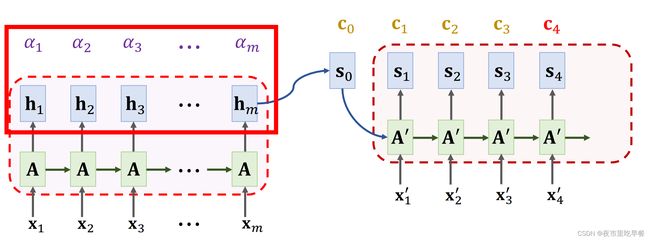
下一步要计算c1，跟之前一样，先计算权重，αi是encoder第i个状态hi与decoder当前状态s1的相关性，把decoder状态s1与encoder所有m个状态进行对比，计算出m个权重，记作α1到αm，注意一下，虽然上一轮计算c0的时候，算出了m个权重α，但是我们不能用那些α，必须要重新计算α，上一轮计算的是h和s0的相关性，这一轮算的是h与s1的相关性，我们使用相同的符号α，然而这个m个权重α跟上一轮算出来的α不是一样的，现在不能重复使用上一轮计算出来的α，有了权重α，就可以计算新的c1，c1是新的。

Decoder接受新的输入x2’，然后要把状态从s1更新到s2，s2是

下一步是计算新的c2，我们要把decoder当前状态s2与encoder所有状态h1到hm做对比，计算出权重α1到αm，有了这些权重，我们计算

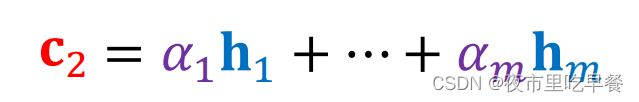现在我们更新s，新的s3，然后计算c3。然后不断重复这个过程，依次更新状态s，计算c，再更新状态s，在计算c，一直到结束。

假设decoder运行了t步，那么一共就m*t个权重α，所以attention的复杂度是m*t，也就是encoder和decoder状态数量的乘积，这个复杂度很高。

Attention为了避免遗忘，大幅提高准确率，代价是巨大的计算。

以上图我们来展示了attention α权重的实际意义，这种下边是encoder，输入是英语，上边是decoder，把英语翻译成法语，attention会把decoder的每个状态与encoder的每个状态做对比，得到两者的相关性，也就是权重α，在这图中，用线连接每个decoder和encoder状态，每条线对应一个权重α，线的粗细表示α的大小，这两个状态之间的线很粗，说明这个权重α很大，两个状态有很高的相关性，这条粗线有很直观的解释，法语里的zone就是英语里的area，所以这两个状态的相似度很高，每当decoder想要生成一个状态的时候，都会看一遍encoder的所有状态，这些权重α告诉decoder应该关注什么地方，这就是attention名字的由来。

三、总结

Seq2seq基于当前状态来生成下一个状态，这样生成的新状态可能已经忘记了encoder的部分输入，如果使用attention，decoder在产生下一个状态之前，会先看一遍encoder的所有状态

因此，decoder就知道encoder的完整信息，并不会遗忘，除了解决遗忘问题，attention还能告诉decoder应该关注encoder的哪一个状态，这就是attention名字的由来

attention可以大幅提高seq2seq的表现，但是attention的缺点就是计算量太大，假设输入encoder的序列长度是m，decoder输出的序列长度是t，标准的seq2seq模型只需要读入一遍输入序列，然后就不会看encoder的输入或者状态，然后decoder依次生成输出序列，所以时间复杂度是m+t，attention的时间复杂度m*t，decoder每一次更新状态都要把encoder的m个状态全都看一遍，所以每一次的时间复杂度是m，decoder自己半身有t个状态，所以总时间复杂度是m*t，使用attention可以提高准确率，但是要付出很大的计算。

四、参考连接

ShusenWang的个人空间_哔哩哔哩_bilibili