LESSON 10.4&10.5&10.6 贝叶斯优化的基本流程&BayesOpt vs HyperOpt vs Optuna batch&基于BayesOpt实现高斯过程gp优化

超参数优化 - 贝叶斯优化方法

import numpy as np
import pandas as pd
import sklearn
import matplotlib as mlp
import matplotlib.pyplot as plt
import seaborn as sns
import time
import re, pip, conda

目录

一 贝叶斯优化基础方法
  1 贝叶斯优化的基本流程
  2 贝叶斯优化用于HPO
二 贝叶斯优化的实现
  1 基于Bayes_opt实现GP优化
  2 基于HyperOpt实现TPE优化
  3 基于Optuna实现多种贝叶斯优化

一 贝叶斯优化基础方法

在之前的课程中我们讲解了网格搜索、随机网格搜索与Halving网格搜索，无论具体每种网格搜索的思想如何变化，网格优化都是在一个大参数空间中、尽量对所有点进行验证后再返回最优损失函数值的方法，这一类方法在计算量与计算时间上有着不可避免的缺陷，因此才会有随机、Halving等试图缩短训练时间、让整体网格搜索更加适合于大型数据和大型空间的手段。然而，尽管sklearn在提高网格搜索效率方面做出了种种优化，但上述方法仍然无法在效率和精度上做到双赢，若希望更快速的进行参数搜索、并且搜索出一组泛化能力尽可能强的参数，目前的常见做法还是选用一些带有先验过程(提前做一些假设)的调参工具，即一些基于贝叶斯过程调参工具。

贝叶斯优化方法是当前超参数优化领域的SOTA手段（State of the Art），可以被认为是当前最为先进的优化框架，它可以被应用于AutoML的各大领域，不止限于超参数搜索HPO的领域，更是可以被用于神经网络架构搜索NAS以及元学习等先进的领域。现代几乎所有在效率和效果上取得优异成果的超参数优化方法都是基于贝叶斯优化的基本理念而形成的，因此贝叶斯优化是整个AutoML中学习的重点。

然而，虽然贝叶斯优化非常强大，但整体的学习难度却非常高。在学习贝叶斯优化之前，学习者不仅需要充分理解机器学习的主要概念和算法、熟悉典型的超参数优化流程，还需要对部分超出微积分、概率论和线性代数的数学知识有所掌握。特别的是，贝叶斯优化算法本身，与贝叶斯优化用于HPO的过程还有区别。在我们课程有限的时间内，我将重点带大家来看贝叶斯优化用于HPO的核心过程。

1 贝叶斯优化的基本流程

首先，我们不理会HPO的问题，先来看待下面的例子。假设现在我们知道一个函数()的表达式以及其自变量的定义域，现在，我们希望求解出的取值范围上()的最小值，你打算如何求解这个最小值呢？面对这个问题，无论是从单纯的数学理论角度，还是从机器学习的角度，我们都已经见过好几个通俗的思路：

• 1 我们可以对()求导、令其一阶导数为0来求解其最小值

函数()f(x)可微，且微分方程可以直接被求解

• 2 我们可以通过梯度下降等优化方法迭代出()的最小值

函数()f(x)可微，且函数本身为凸函数

• 3 我们将全域的带入()计算出所有可能的结果，再找出最小值

函数()f(x)相对不复杂、自变量维度相对低、计算量可以承受

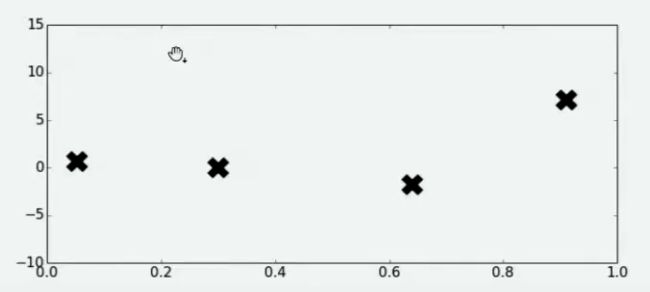
当我们知道函数()的表达式时，以上方法常常能够有效，但每个方法都有自己的前提条件。假设现在函数()是一个平滑均匀的函数，但它异常复杂、且不可微，我们无法使用上述三种方法中的任意一种方法求解，但我们还是想求解其最小值，可以怎么办呢？由于函数异常复杂，带入任意计算的所需的时间很长，所以我们不太可能将全域都带入进行计算，但我们还是可以从中随机抽样部分观测点来观察整个函数可能存在的趋势。于是我们选择在的定义域上随机选择了4个点，并将4个点带入()进行计算，得到了如下结果：

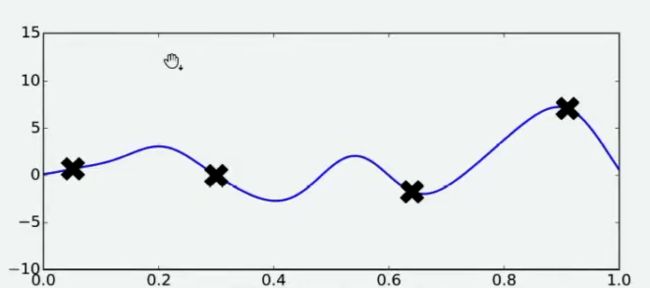
 好了，现在有了这4个观测值，你能告诉我()的最小值在哪里吗？你认为最小值点可能在哪里呢？大部分人会倾向于认为，最小值点可能非常接近于已观测出4个()值中最小的那个值，但也有许多人不这么认为。当我们有了4个观测值，并且知道我们的函数时相对均匀、平滑的函数，那我们可能对函数的整体分布有如下猜测：

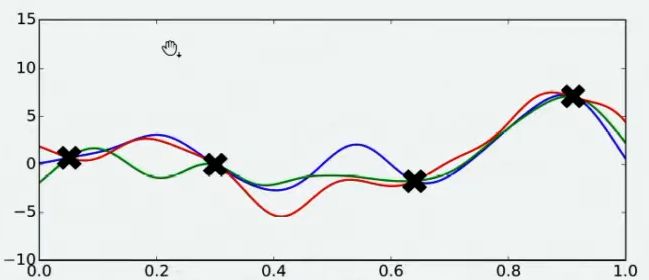
当我们对函数整体分布有一个猜测时，这个分布上一定会存在该函数的最小值。同时，不同的人可能对函数的整体分布有不同的猜测，不同猜测下对应的最小值也是不同的。

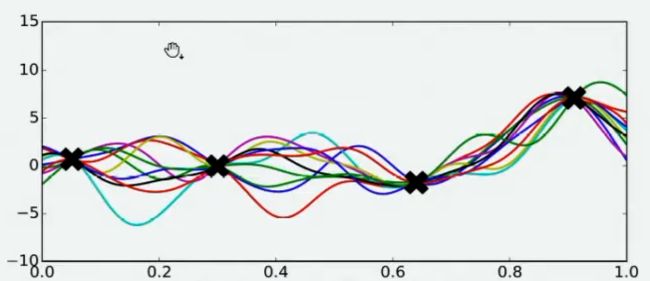
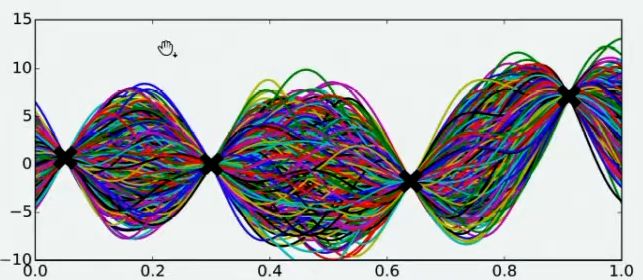
现在，假设我们邀请了数万个人对该问题做出猜测，每个人所猜测的曲线如下图所示。不难发现，在观测点的附近，每个人猜测的函数值差距不大，但是在远离远侧点的地方，每个人猜测的函数值就高度不一致了。这也是当然的，因为观测点之间函数的分布如何完全是未知的，并且该分布离观测点越远时，我们越不确定真正的函数值在哪里，因此人们猜测的函数值的范围非常巨大。

[0,1] - 100个小区间

[0,0.01] n1
[0.01,0.02] n2
[0.02,0.03] n3
...
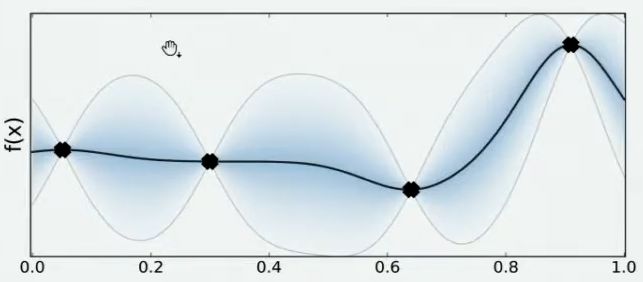
[0.99,1] n100

现在，我们将所有猜测求均值，并将任意均值周围的潜在函数值所在的区域用色块表示，可以得到一条所有人猜测的平均曲线。不难发现，色块所覆盖的范围其实就是大家猜测的函数值的上界和下界，而任意所对应的上下界差异越大，表示人们对函数上该位置的猜测值的越不确定。因此上下界差异可以衡量人们对该观测点的置信度（自信度），色块范围越大，置信度越低。

在观测点周围，置信度总是很高的，远离观测点的地方，置信度总是很低，所以如果我们能够在置信度很低的地方补充一个实际的观测点，我们就可以很快将众人的猜测统一起来。以下图为例，当我们在置信度很低的区间内取一个实际观测值时，围绕该区间的“猜测”会立刻变得集中，该区间内的置信度会大幅升高。

当整个函数上的置信度都非常高时，我们可以说我们得出了一条与真实的()曲线高度相似的曲线∗，次数我们就可以将∗的最小值当作真实()的最小值来看待。自然，如果估计越准确，∗越接近()，则∗的最小值也会越接近于()的真实最小值。那如何才能够让∗更接近()呢？根据我们刚才提升置信度的过程，很明显——观测点越多，我们估计出的曲线会越接近真实的()。然而，由于计算量有限，我们每次进行观测时都要非常谨慎地选择观测点。那现在，如何选择观测点才能够最大程度地帮助我们估计出()的最小值呢？

有非常多的方法，其中最简单的手段是使用最小值出现的频数进行判断。由于不同的人对函数的整体分布有不同的猜测，不同猜测下对应的最小值也是不同的，根据每个人猜测的函数结果，我们在轴上将定义域区间均匀划分为100个小区间，如果有某个猜测的最小值落在其中一个区间中，我们就对该区间进行计数（这个过程跟对离散型变量绘制直方图的过程完全一致）。当有数万个人进行猜测之后，我们同时也绘制了基于轴上不同区间的频数图，频数越高，说明猜测最小值在该区间内的人越多，反之则说明该猜测最小值在该区间内的人越少。该频数一定程度上反馈出最小值出现的概率，频数越高的区间，函数真正的最小值出现的概率越高。

当我们将轴上的区间划分得足够细后，绘制出的频数图可以变成概率密度曲线，曲线的最大值所对应的点是()的最小值的概率最高，因此很明显，我们应该将曲线最大值所对应的点确认为下一个观测点。根据图像，我们知道最小值最有可能在的区间就在x=0.7左右的位置。当我们不取新的观测点时，现在()上可以获得的可靠的最小值就是x=0.6时的点，但我们如果在x=0.7处取新的观测值，我们就很有可能找到比当前x=0.6的点还要小的。因此，我们可以就此决定，在x=0.7处进行观测。

当我们在x=0.7处取出观测值之后，我们就有了5个已知的观测点。现在，我们再让数万人根据5个已知的观测点对整体函数分布进行猜测，猜测完毕之后再计算当前最小值频数最高的区间，然后再取新的观测点对()进行计算。当允许的计算次数被用完之后（比如，500次），整个估计也就停止了。

你发现了吗？在这个过程当中，我们其实在不断地优化我们对目标函数()的估计，虽然没有对()进行全部定义域上的计算，也没有找到最终确定一定是()分布的曲线，但是随着我们观测的点越来越多，我们对函数的估计是越来越准确的，因此也有越来越大的可能性可以估计出()真正的最小值。这个优化的过程，就是贝叶斯优化。

2 贝叶斯优化用于HPO

在贝叶斯优化的数学过程当中，我们主要执行以下几个步骤：

• 1 定义需要估计的()以及的定义域

• 2 取出有限的n个上的值，求解出这些对应的()（求解观测值）

• 3 根据有限的观测值，对函数进行估计（该假设被称为贝叶斯优化中的先验知识），得出该估计∗上的目标值（最大值或最小值）

• 4 定义某种规则，以确定下一个需要计算的观测点

并持续在2-4步骤中进行循环，直到假设分布上的目标值达到我们的标准，或者所有计算资源被用完为止（例如，最多观测m次(最多观测m个点)，或最多允许运行t分钟）。

---

以上流程又被称为序贯模型优化（SMBO），是最为经典的贝叶斯优化方法。在实际的运算过程当中，尤其是超参数优化的过程当中，有以下具体细节需要注意：

• 当贝叶斯优化不被用于HPO时，一般()可以是完全的黑盒函数（black box function，也译作黑箱函数，即只知道与()的对应关系，却丝毫不知道函数内部规律、同时也不能写出具体表达式的一类函数），因此贝叶斯优化也被认为是可以作用于黑盒函数估计的一类经典方法。但在HPO过程当中，需要定义的()一般是交叉验证的结果/损失函数的结果，而我们往往非常清楚损失函数的表达式，只是我们不了解损失函数内部的具体规律，因此HPO中的()不能算是严格意义上的黑盒函数。

• 在HPO中，自变量就是超参数空间。在上述二维图像表示中，为一维的，但在实际进行优化时，超参数空间往往是高维且极度复杂的空间。

• 最初的观测值数量n、以及最终可以取到的最大观测数量m都是贝叶斯优化的超参数，最大观测数量m也决定了整个贝叶斯优化的迭代次数。

• 在第3步中，根据有限的观测值、对函数分布进行估计的工具被称为概率代理模型（Probability Surrogate model），毕竟在数学计算中我们并不能真的邀请数万人对我们的观测点进行连线。这些概率代理模型自带某些假设，他们可以根据廖廖数个观测点估计出目标函数的分布∗（包括∗上每个点的取值以及该点对应的置信度）。在实际使用时，概率代理模型往往是一些强大的算法，最常见的比如高斯过程、高斯混合模型等等。传统数学推导中往往使用高斯过程，但现在最普及的优化库中基本都默认使用基于高斯混合模型的TPE过程。（高斯过程估计均值方差来得到∗上每个点的取值以及该点对应的置信度）

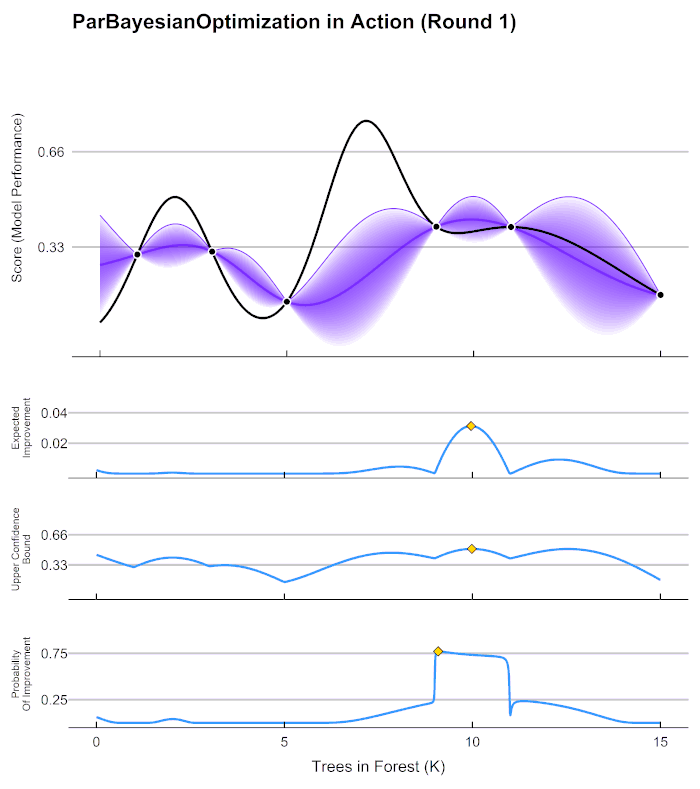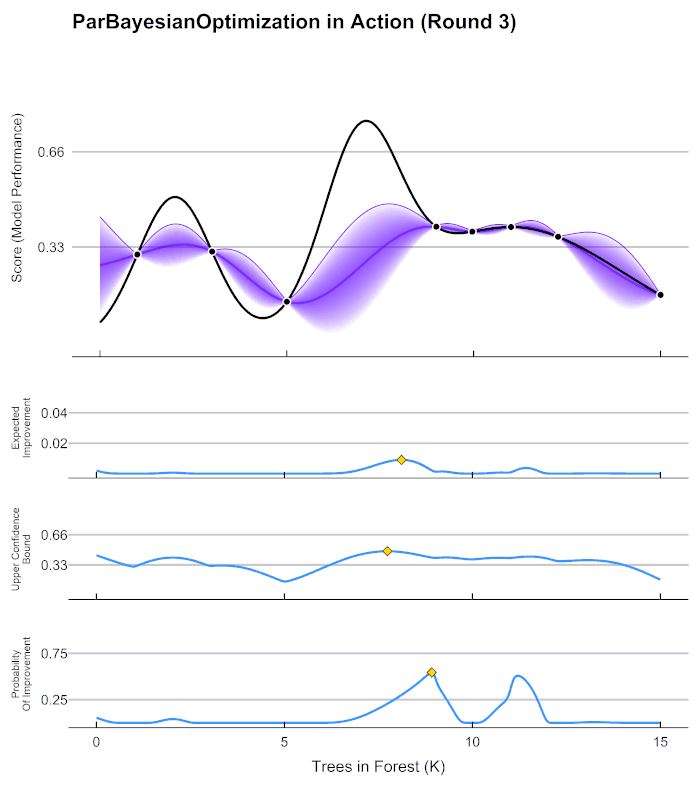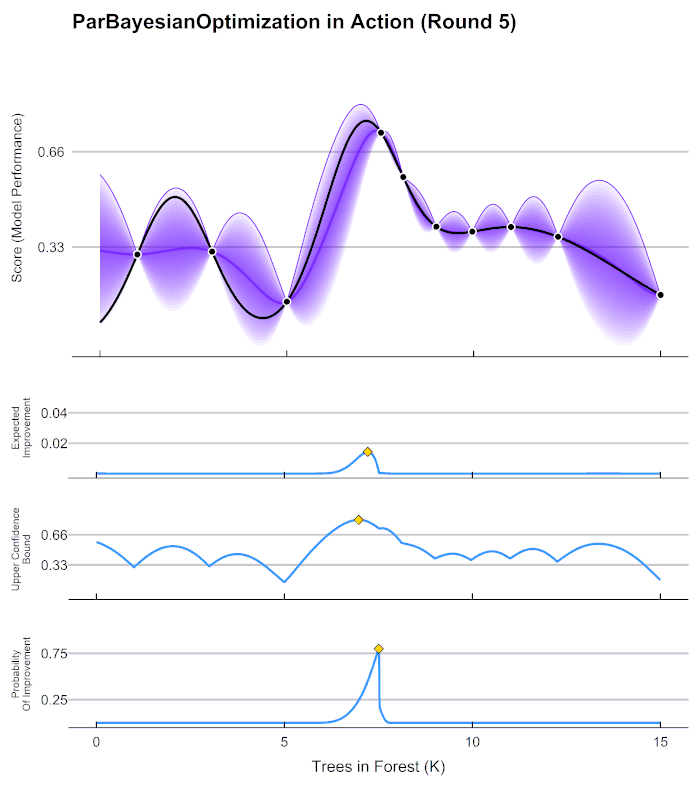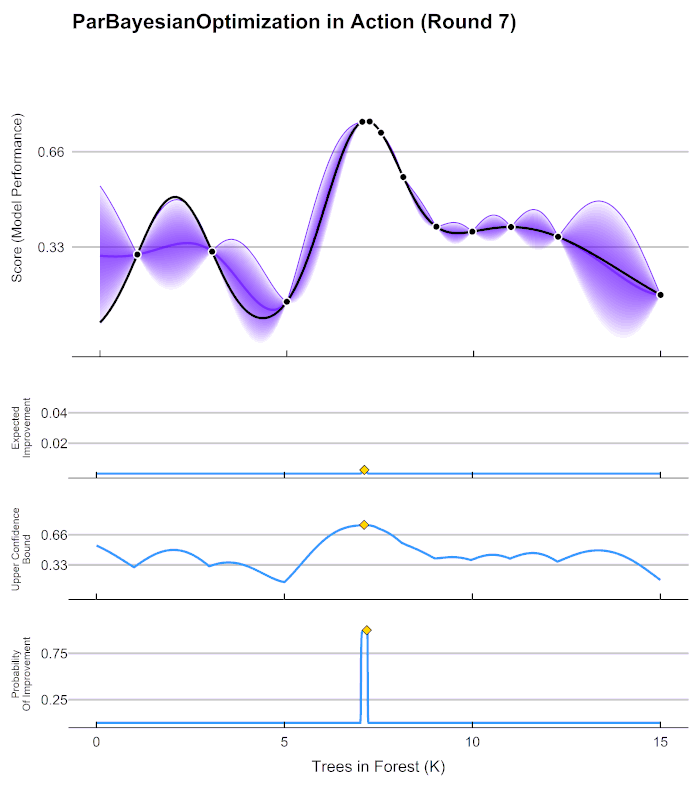
• 在第4步中用来确定下一个观测点的规则被称为采集函数（Aquisition Function），采集函数衡量观测点对拟合∗所产生的影响，并选取影响最大的点执行下一步观测，因此我们往往关注采集函数值最大的点。最常见的采集函数主要是概率增量PI（Probability of improvement，比如我们计算的频数）、期望增量（Expectation Improvement）、置信度上界（Upper Confidence Bound）、信息熵（Entropy）等等。上方gif图像当中展示了PI、UCB以及EI。其中大部分优化库中默认使用期望增量。

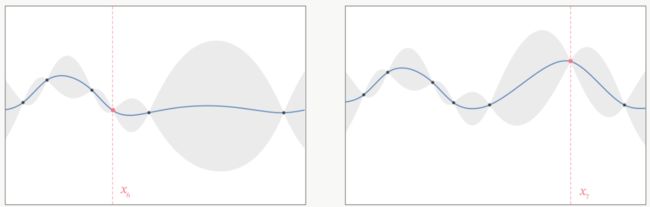
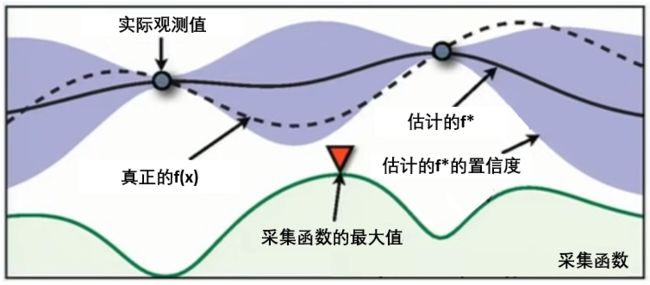
在HPO中使用贝叶斯优化时，我们常常会看见下面的图像，这张图像表现了贝叶斯优化的全部基本元素，我们的目标就是在采集函数指导下，让∗尽量接近()。

真正的f(x)（虚线）上取两个观测值，利用概率代理模型来推测出估计的f*（实线）和置信度。根据概率代理模型所输出的结果（f*）计算出采集函数，采集函数最大值所对应的x点就是下一个观测点。

现在我们已经了解贝叶斯优化的基本流程。与许多算法一样，基础流程足以支撑我们使用已经搭建好的优化库进行超参数优化了，即便我们没有对优化原理的每个细节都了如指掌，我们也可以通过实验反馈出的结果来直接判断是否应该调整我们的代码。接下来，我们会先学习如何应用贝叶斯优化的各类库实现不同的贝叶斯优化算法。

二 贝叶斯优化的实现

贝叶斯优化是当今黑盒函数估计领域最为先进和经典的方法，在同一套序贯模型下使用不同的代理模型以及采集函数、还可以发展出更多更先进的贝叶斯优化改进版算法，因此，贝叶斯优化的其算法本身就多如繁星，实现各种不同种类的贝叶斯优化的库也是琳琅满目，几乎任意一个专业用于超参数优化的工具库都会包含贝叶斯优化的内容。我们可以在以下页面找到大量可以实现贝叶斯优化方法的HPO库：AutoML | Overview of HPO Packages ，其中大部分库都是由独立团队开发和维护，因此不同的库之间之间的优劣、性格、功能都有很大的差异。在课程中，我们将介绍如下三个可以实现贝叶斯优化的库：bayesian-optimization，hyperopt，optuna。

注意，以上三个库都不支持基于Python环境的并行或加速，大多数优化算法库只能够支持基于数据库（如MangoDB，mySQL）的并行或加速，但以上库都可以被部署在分布式计算平台。

三个库极其辅助包的安装方法分别如下，使用pip或conda安装时注意关闭梯子。

• Bayes_opt

#!pip install bayesian-optimization
#!conda install -c conda-forge bayesian-optimization

• Hyperopt

#!pip install hyperopt

• Optuna

#!pip install optuna
#!conda install -c conda-forge optuna

• Skopt（作为Optuna辅助包安装，也可单独使用）

#!pip install scikit-optimize

接下来我们会分别使用三个库来实现贝叶斯优化。在课程中，我们依然使用集成算法中的房价数据作为验证数据，并且呈现出我们之前在不同优化方法上得出的结果作为对比。同时，我们将使用与集成算法中完全一致的随机数种子、以及随机森林算法作为被优化的评估器。

• 导入库，确认使用数据

#基本工具
import numpy as np
import pandas as pd
import time
import os #修改环境设置

#算法/损失/评估指标等
import sklearn
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import KFold, cross_validate

#优化器
from bayes_opt import BayesianOptimization

import hyperopt
from hyperopt import hp, fmin, tpe, Trials, partial
from hyperopt.early_stop import no_progress_loss

import optuna

Bayes_opt版本：1.2.0

print(optuna.__version__)
#2.10.0

print(hyperopt.__version__)
#0.2.7

data = pd.read_csv(r"D:\Pythonwork\2021ML\PART 2 Ensembles\datasets\House Price\train_encode.csv",index_col=0)

X = data.iloc[:,:-1]
y = data.iloc[:,-1]
X.head()

X.shape
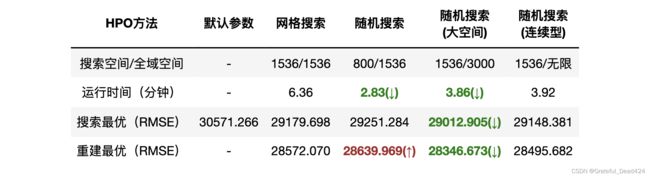
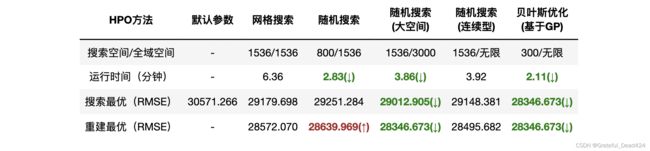
#(1460, 80)

• 确认该数据集上的历史成果

1 基于Bayes_opt实现GP优化

bayes-optimization是最早开源的贝叶斯优化库之一，也是为数不多至今依然保留着高斯过程优化的优化库。由于开源较早、代码简单，bayes-opt常常出现在论文、竞赛kernels或网络学习材料当中，因此理解Bayes_opt的代码是极其重要的课题。不过，bayes-opt对参数空间的处理方式较为原始，也缺乏相应的提效/监控功能，对算力的要求较高，因此它往往不是我们进行优化时的第一首选库。通常来说，当且仅当我们必须要实现基于高斯过程的贝叶斯优化，且算法的参数空间中带有大量连续型参数时，我们才会优先考虑Bayes_opt库。我们可以在github上找到bayes-optmization的官方文档（https://github.com/fmfn/BayesianOptimization） ，想要进一步了解其基本功能与原理的小伙伴可以进行阅读。

from bayes_opt import BayesianOptimization

• 1 定义目标函数

目标函数的值即()的值。贝叶斯优化会计算()在不同上的观测值，因此()的计算方式需要被明确。在HPO过程中，我们希望能够筛选出令模型泛化能力最大的参数组合，因此()应该是损失函数的交叉验证值或者某种评估指标的交叉验证值。需要注意的是，bayes_opt库存在三个影响目标函数定义的规则：

1 目标函数的输入必须是具体的超参数，而不能是整个超参数空间，更不能是数据、算法等超参数以外的元素，因此在定义目标函数时，我们需要让超参数作为目标函数的输入。

2 超参数的输入值只能是浮点数，不支持整数与字符串。因此当算法的实际参数需要输入字符串时，该参数不能使用bayes_opt进行调整，当算法的实际参数需要输入整数时，则需要在目标函数中规定参数的类型。

3 bayes_opt只支持寻找()的最大值，不支持寻找最小值。因此当我们定义的目标函数是某种损失时，目标函数的输出需要取负（即，如果使用RMSE，则应该让目标函数输出负RMSE，这样最大化负RMSE后，才是最小化真正的RMSE。）当我们定义的目标函数是准确率，或者auc等指标，则可以让目标函数的输出保持原样。

def bayesopt_objective(n_estimators,max_depth,max_features,min_impurity_decrease):
    
    #定义评估器
    #需要调整的超参数等于目标函数的输入，不需要调整的超参数则直接等于固定值
    #默认参数输入一定是浮点数，因此需要套上int函数处理成整数
    reg = RFR(n_estimators = int(n_estimators)
              ,max_depth = int(max_depth)
              ,max_features = int(max_features)
              ,min_impurity_decrease = min_impurity_decrease
              ,random_state=1412
              ,verbose=False #可自行决定是否开启森林建树的verbose
              ,n_jobs=-1)
    
    #定义损失的输出，5折交叉验证下的结果，输出负根均方误差（-RMSE）
    #注意，交叉验证需要使用数据，但我们不能让数据X,y成为目标函数的输入
    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    validation_loss = cross_validate(reg,X,y
                                     ,scoring="neg_root_mean_squared_error"
                                     ,cv=cv
                                     ,verbose=False
                                     ,n_jobs=-1
                                     ,error_score='raise'
                                     #如果交叉验证中的算法执行报错，则告诉我们错误的理由
                                    )
    
    #交叉验证输出的评估指标是负根均方误差，因此本来就是负的损失
    #目标函数可直接输出该损失的均值
    return np.mean(validation_loss["test_score"])

• 2 定义参数空间

在任意超参数优化器中，优化器会将参数空格中的超参数组合作为备选组合，一组一组输入到算法中进行训练。在贝叶斯优化中，超参数组合会被输入我们定义好的目标函数()中。

在bayes_opt中，我们使用字典方式来定义参数空间，其中参数的名称为键，参数的取值范围为值。且任意参数的取值范围为双向闭区间，以下方的空间为例，在n_estimators的取值中，80与100都可以被取到。

以下参数空间与我们在随机森林中获得最高分的随机搜索的范围高度相似。

param_grid_simple = {'n_estimators': (80,100)
                     , 'max_depth':(10,25)
                     , "max_features": (10,20)
                     , "min_impurity_decrease":(0,1)
                    }

需要注意的是，bayes_opt只支持填写参数空间的上界与下界，不支持填写步长等参数，且bayes_opt会将所有参数都当作连续型超参进行处理，因此bayes_opt会直接取出闭区间中任意浮点数作为备选参数。例如，取92.28作为n_estimators的值。

这也是为什么在目标函数中，我们需要对整数型超参的取值都套上int函数。假设优化器取出92.28作为n_estimators的值，实际传入随机森林算法的会是int(92.28) = 92，如此我们可以保证算法运行过程中不会因参数类型不符而报错。也因为bayes_opt的这个性质，输入bayes_opt的参数空间天生会比其他贝叶斯优化库更大/更密，因此需要的迭代次数也更多。

• 3 定义优化目标函数的具体流程

在有了目标函数与参数空间之后，我们就可以按bayes_opt的规则进行优化了。在任意贝叶斯优化算法的实践过程中，一定都有涉及到随机性的过程——例如，随机抽取点作为观测点，随机抽样部分观测点进行采集函数的计算等等。在大部分优化库当中，这种随机性是无法控制的，即便允许我们填写随机数种子，优化算法也不能固定下来。因此我们可以尝试填写随机数种子，但需要记住优化算法每次运行时一定都会不一样。

虽然，优化算法无法被复现，但是优化算法得出的最佳超参数的结果却是可以被复现的。只要优化完毕之后，可以从优化算法的实例化对象中取出最佳参数组合以及最佳分数，该最佳参数组合被输入到交叉验证中后，是一定可以复现其最佳分数的。如果没能复现最佳分数，则是交叉验证过程的随机数种子设置存在问题，或者优化算法的迭代流程存在问题。（GridSearchCV--自己帮我们分割数据集、自己帮我们进行交叉验证，自己求解出结果，通常会获取最佳参数自己（分割数据集、进行交叉验证，求解出结果）再验证一次，所以搜索最优和重建最优是不同的。然而对于bayes优化而言没有GridSearchCV搜索最优和重建最优是相同的）

def param_bayes_opt(init_points,n_iter):
    
    #定义优化器，先实例化优化器
    opt = BayesianOptimization(bayesopt_objective #需要优化的目标函数
                               ,param_grid_simple #备选参数空间
                               ,random_state=1412 #随机数种子，虽然无法控制住
                              )
    
    #使用优化器，记住bayes_opt只支持最大化
    opt.maximize(init_points = init_points #抽取多少个初始观测值
                 , n_iter=n_iter #一共观测/迭代多少次
                )
    
    #优化完成，取出最佳参数与最佳分数
    params_best = opt.max["params"]
    score_best = opt.max["target"]
    
    #打印最佳参数与最佳分数
    print("\n","\n","best params: ", params_best,
          "\n","\n","best cvscore: ", score_best)
    
    #返回最佳参数与最佳分数
    return params_best, score_best

• 4 定义验证函数（非必须）

优化后的结果是可以复现的，即我们可以对优化算法给出的最优参数进行再验证，其中验证函数与目标函数高度相似，输入参数或超参数空间、输出最终的损失函数结果。在使用sklearn中自带的优化算法时，由于优化算法自己会执行分割数据、交叉验证的步骤，因此优化算法得出的最优分数往往与我们自身验证的分数不同（因为交叉验证时的数据分割不同）。然而在贝叶斯优化过程中，目标函数中的交叉验证即数据分割都是我们自己规定的，因此原则上来说，只要在目标函数中设置了随机数种子，贝叶斯优化给出的最佳分数一定与我们验证后的分数相同，所以当你对优化过程的代码比较熟悉时，可以不用进行二次验证。

def bayes_opt_validation(params_best):
    
    reg = RFR(n_estimators = int(params_best["n_estimators"]) 
              ,max_depth = int(params_best["max_depth"])
              ,max_features = int(params_best["max_features"])
              ,min_impurity_decrease = params_best["min_impurity_decrease"]
              ,random_state=1412
              ,verbose=False
              ,n_jobs=-1)

    cv = KFold(n_splits=5,shuffle=True,random_state=1412)
    validation_loss = cross_validate(reg,X,y
                                     ,scoring="neg_root_mean_squared_error"
                                     ,cv=cv
                                     ,verbose=False
                                     ,n_jobs=-1
                                    )
    return np.mean(validation_loss["test_score"])

• 5 执行实际优化流程

start = time.time()
params_best, score_best = param_bayes_opt(20,280) #初始看20个观测值，后面迭代280次
print('It takes %s minutes' % ((time.time() - start)/60))
validation_score = bayes_opt_validation(params_best)
print("\n","\n","validation_score: ",validation_score)
# |   iter    |  target   | max_depth | max_fe... | min_im... | n_esti... |
# -------------------------------------------------------------------------
# |  1        | -2.948e+0 |  23.2     |  17.52    |  0.06379  |  88.79    |
# |  2        | -2.909e+0 |  14.8     |  17.61    |  0.9214   |  97.58    |
# |  3        | -2.9e+04  |  15.86    |  15.56    |  0.2661   |  87.98    |
# |  4        | -2.887e+0 |  14.05    |  16.84    |  0.06744  |  89.72    |
#  ......
# |  297      | -2.895e+0 |  22.89    |  19.95    |  0.6566   |  91.44    |
# |  298      | -2.975e+0 |  10.13    |  13.87    |  0.9502   |  81.74    |
# |  299      | -2.946e+0 |  16.58    |  15.55    |  0.01365  |  99.89    |
# |  300      | -2.888e+0 |  24.79    |  19.88    |  0.8136   |  88.76    |
# =========================================================================

 
#  best params:  {'max_depth': 22.76987255830374, 'max_features': 14.139404019924546, 'min_impurity_decrease': 0.0, 'n_estimators': 89.82134842869006} 
#  best cvscore:  -28346.672687223065
# It takes 2.107581957181295 minutes
#  validation_score:  -28346.672687223065

• 原理上有优越性

可以看到，基于高斯过程的贝叶斯优化在2.11分钟内锁定了最佳分数28346.673，这是之前使用随机搜索时获得的最佳分数，很可能也是我们当前超参数空间上可以获得的最佳分数。贝叶斯优化作为从原理上高于网格优化的HPO方法，能够以更短的时间获得与随机网格搜索相同的结果，可见其原理上的优越性。

• 优化过程无法复现，但优化结果可以复现

但同时要注意，由于贝叶斯优化每次都是随机的，因此我们并不能在多次运行代码时复现出28346.673这个结果，事实上如果我们重复运行，也只有很小的概率可以再次找到这个最低值（这一点对于随机搜索来说也是类似的，如果不规定随机数种子，我们也无法复现最低值）。因此我们在执行贝叶斯优化时，往往会多运行几次观察模型找出的结果。同时，验证分数与目标函数最后输出的分数一模一样，可见最终输出的超参数组合的效力是可以复现的。

• 效率不足

不难发现，bayes_opt的速度虽然快，效率却不高。实际上在迭代到170次时，贝叶斯优化就已经找到了最小损失，但由于没有提前停止机制，模型还持续地迭代了130次才停下，如果bayes_opt支持提前停止机制，贝叶斯优化所需的实际迭代时间可能会更少。同时，由于Bayes_opt只能够在参数空间提取浮点数，bayes_opt在随机森林上的搜索效率是较低的，即便在10次不同的迭代中分别取到了[88.89, 88.23, 88.16, 88.59……]等值，在取整之后也只能够获得一个备选值88，但bayes_opt无法辨别这种区别，因此可能取出了众多无效的观测点。如果使用其他贝叶斯优化器，贝叶斯优化的效率将会更高。

• 支持灵活修改

虽然在我们的代码中没有体现，但bayes_opt是支持灵活修改采集函数与高斯过程中的种种参数的，具体可以参考这里：BayesianOptimization/advanced-tour.ipynb at master · fmfn/BayesianOptimization · GitHub