NOTE(二): Deep Learning

《详解深度学习》笔记（二）：多层感知机解决异或问题

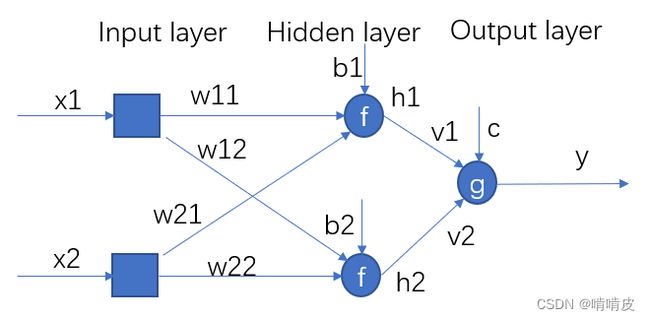
结构

更新方法

1.定义每层激活前的值
$$\begin{gathered} p=wx+b \\ q=vh+c \\ h=f(p) \end{gathered}$$
2. 权值更新
$$\begin{gathered} E(v,c)=-\sum _{n=1}^N(t_{n}log{y}_n+(1-t_n)log(1-y_n)) \\ {y}_n=f(q)=f(vh+c) \end{gathered}$$
计算误差函数和逻辑回归方法一样，同样是构造似然函数，取其相反数，将最大化问题转换为最小化问题。
$$\{\begin{array}{l}\frac{\partial E}{\partial v}=\frac{\partial E}{\partial q}\frac{\partial q}{\partial v}=-({\sum }_{n=1}^N(t_n-y_n))\ast h\\ \frac{\partial E}{\partial c}=\frac{\partial E}{\partial q}\frac{\partial q}{\partial c}=-{\sum }_{n=1}^N(t_n-y_n)\end{array}$$
然后根据反向传播法，求w,b的梯度。

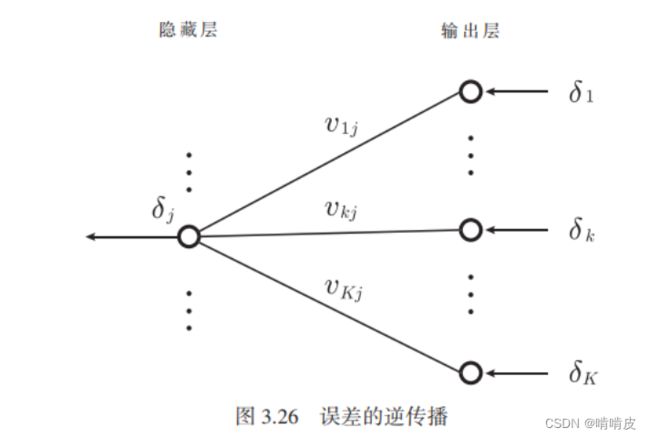
$$\{\begin{array}{l}\frac{\partial E}{\partial w}=\frac{\partial E}{\partial p}\frac{\partial p}{\partial w}=\frac{\partial E}{\partial q}\frac{\partial q}{\partial p}x=\frac{\partial E}{\partial q}(v\ast f\prime (p))x=-({\sum }_{n=1}^N(t_n-y_n))(v\ast f\prime (p))x\\ \frac{\partial E}{\partial b}=\frac{\partial E}{\partial p}\frac{\partial p}{\partial b}=\frac{\partial E}{\partial q}\frac{\partial q}{\partial p}=\frac{\partial E}{\partial q}(v\ast f\prime (p))=-({\sum }_{n=1}^N(t_n-y_n))(v\ast f\prime (p))\end{array}，值得注意的是，f\prime (p)是矩阵对矩阵求导$$

代码

1.初始化

X=[0 0;
   1 0;
   0 1;
   1 1];
T=[0 1 1 0];

N=300;
w=[0.1 0.1;
   0.1 0.1];
v=[0.1;-0.1];
b=[0;0];
c=0;
eta=0.1;
sum_w=zeros(2,2);
sum_v=zeros(2,1);
sum_b=zeros(2,1);
sum_c=0;

2.训练

for i=1:N
    for j=1:4
        p=w*(X(j,:))'+b;
        p1=p(1,1);
        p2=p(2,1);
        fp(1,1)=sigmoid(p1);
        fp(1,2)=sigmoid(p2);
        q=v(1,1)*fp(1,1)+v(2,1)*fp(1,2)+c;
        y=sigmoid(q);
        delta_v=(T(j)-y)*fp';
        delta_c=(T(j)-y);
        dq_dp11=v(1,1)*sigmoid(p1)*(1-sigmoid(p1));
        dq_dp22=v(2,1)*sigmoid(p2)*(1-sigmoid(p2));
        dq_dp=[dq_dp11;dq_dp22];
        delta_w=delta_c*dq_dp*X(j,:);
        delta_b=delta_c*dq_dp;
        sum_w=sum_w+delta_w;
        sum_b=sum_b+delta_b;
        sum_v=sum_v+delta_v;
        sum_c=sum_c+delta_c;
    end
    w=w+sum_w*eta;
    v=v+sum_v*eta;
    b=b+sum_b*eta;
    c=c+sum_c*eta;
end

3.测试

for k=1:4
        p=w*(X(k,:))'+b;                                                
        p1=p(1,1);
        p2=p(2,1);
        fp(1,1)=sigmoid(p1);
        fp(1,2)=sigmoid(p2);
        q=v(1,1)*fp(1,1)+v(2,1)*fp(1,2)+c;
        Y(k)=sigmoid(q);
        P(:,k)=p;
        FP(k,:)=fp;
        Q(k)=q;
end
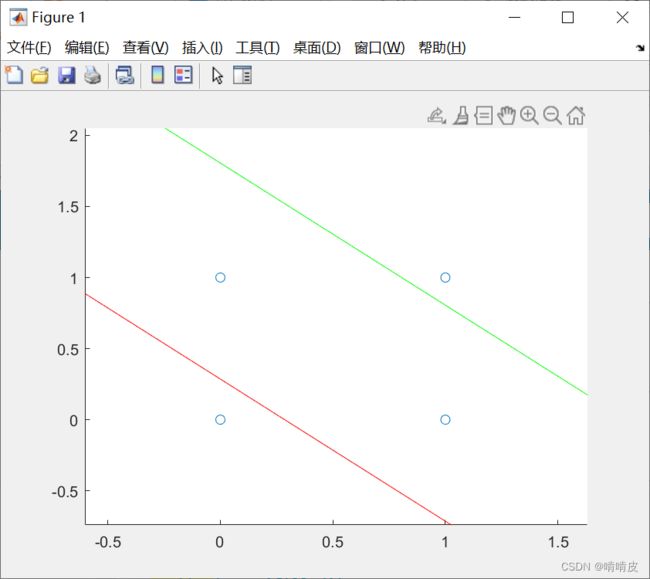
scatter(X(:,1),X(:,2));
hold on 
XX=-10:1:10;
Y1=-1*w(1,1)/w(1,2)*XX-b(1,1)/w(1,2);
Y2=-1*w(2,1)/w(2,2)*XX-b(2,1)/w(2,2);
plot(XX,Y1,'r',XX,Y2,'g');
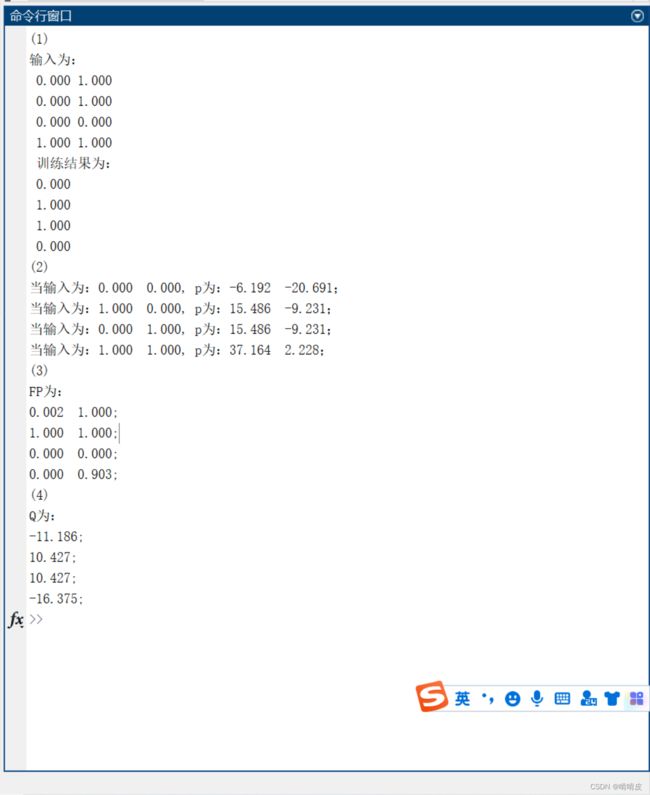
fprintf('(1)\n输入为：\n %4.3f %4.3f \n %4.3f %4.3f \n %4.3f %4.3f \n %4.3f %4.3f \n 训练结果为： \n %4.3f \n %4.3f \n %4.3f \n %4.3f \n',X,Y);
fprintf('(2)\n当输入为：%4.3f  %4.3f, p为：%4.3f  %4.3f；\n当输入为：%4.3f  %4.3f, p为：%4.3f  %4.3f；\n当输入为：%4.3f  %4.3f, p为：%4.3f  %4.3f；\n当输入为：%4.3f  %4.3f, p为：%4.3f  %4.3f；\n',X(1,:),P(:,1),X(2,:),P(:,2),X(3,:),P(:,3),X(4,:),P(:,4));
fprintf('(3)\nFP为：\n%4.3f  %4.3f;\n%4.3f  %4.3f;\n%4.3f  %4.3f;\n%4.3f  %4.3f;\n',FP);
fprintf('(4)\nQ为：\n%4.3f;\n%4.3f;\n%4.3f;\n%4.3f;\n',Q);

结果

分析

从以上结果可以看出第一个权值w将输入的数据通过两条线进行了划分，分了三类。而第二个权值则进一步将其分为两类。