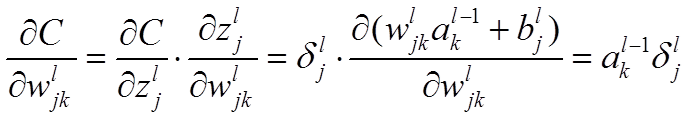机器学习前向传播,反向传播
吴恩达机器学习<三>
- 一、神经网络
- 二、前向传播算法
- 2.反向传播算法
-
- 代价函数
- 推导过程
- 代码实现
一、神经网络
神经网络是模仿大脑神经元,建立的模型。模型中的每个神经元都是一个单独的【学习模型】,这些神经元也叫做激活单元(activation unit)

Sigmoid函数在之前的逻辑回归中有写到,这里就不多写了,在上述图中,它将左边输入的和参数θ相乘后作为输入,经过自身的计算得到结果 h 0 ( x ) h_0(x) h0(x),在神经网络中,参数又可被成为权重(weight)。
二、前向传播算法
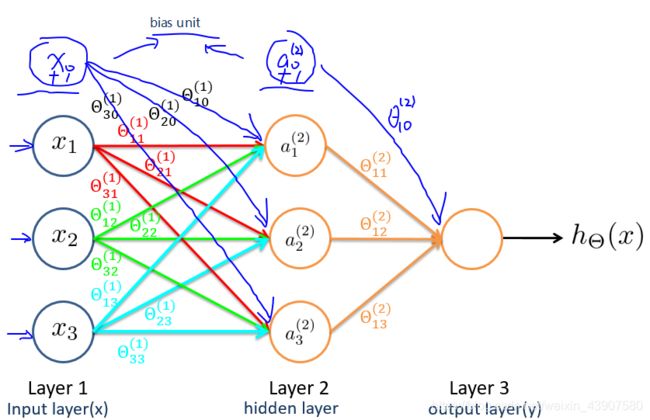
x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3成为输入层, a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3成为隐藏层,最后一层成为输出层。
每次通过权重计算之后,需要用激活函数计算
θ m n i \theta_{mn}^i θmni表示第i层参数矩阵,m对应第i+1层激活,n对应第i层激活单元
a i ( j ) a_i^{(j)} ai(j)表示的是第i层第j个激活单元
g ( z ) g(z) g(z)表示激活函数
输出层表达式:
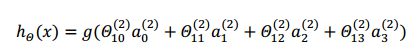
从上面的图和公式可以看出,从输入层开始,不断的通过参数矩阵的运算,最后到输出层,这样的一个过程就叫前向传播算法。
神经网络和逻辑回归/线性回归的比较:
我们可以把神经网络中的隐藏层的激活单元看成是输入特征的更加高级的特征值,这些特征值可以通过之后的反向传播不断优化,调整,而逻辑回归中我们只能限制的使用原始特征(相当于神经网络的输入层)
2.反向传播算法
反向传播算法思想:
- 将训练集数据输入到神经网络的输入层,经过隐藏层,最后达到输出层并输出结果,这是ANN的前向传播过程;
- 由于ANN的输出结果与实际结果有误差,则计算估计值与实际值之间的误差,并将该误差从输出层向隐藏层反向传播,直至传播到输入层;
- 在反向传播的过程中,根据误差调整各种参数的值;不断迭代上述过程,直至收敛

ω j k l \omega_{jk}^l ωjkl表示 l − 1 l-1 l−1层的第k个神经元连接到第 l l l层的第 j j j个神经元的额权重。
b j l b_j^l bjl表示第 l l l层的第 j j j个神经元的偏置
z j l z_j^l zjl表示第 l l l层的第 j j j个神经元的输入
z = α ω z = \alpha\omega z=αω(向量运算)
α j l \alpha_j^l αjl表示第 l l l层的第 j j j个神经元的输出
α = σ ( z ) \alpha=\sigma(z) α=σ(z)( σ ′ ( z ) \sigma^{'}(z) σ′(z)表示激活函数)
代价函数
代价函数被用来计算神经网络输出值与实际值之间的误差。根据这个误差来调整参数。
C = 1 2 n ∑ ∥ y ( x ) − α L ( x ) ∥ 2 C = \frac{1}{2n}\sum\lVert \ y(x)-\alpha^L(x)\rVert ^2 C=2n1∑∥ y(x)−αL(x)∥2
推导过程
- 最后一层神经网络产生的误差
δ L = ∂ C ∂ z L = ∂ C ∂ α L ∂ α L ∂ z L = ∂ C ∂ α L σ ′ ( z L ) \delta^L=\frac{\partial C}{\partial z^L}=\frac{\partial C}{\partial \alpha ^L}\frac{\partial \alpha ^L}{\partial z ^L}=\frac{\partial C}{\partial \alpha ^L}\sigma^{'}(z^L) δL=∂zL∂C=∂αL∂C∂zL∂αL=∂αL∂Cσ′(zL)
代码实现
前向传播
def forward_propagate(X, theta1, theta2):
m = X.shape[0]
a1 = np.insert(X, 0, values=np.ones(m), axis=1)
z2 = a1 * theta1.T
a2 = np.insert(sigmoid(z2), 0, values=np.ones(m), axis=1)
z3 = a2 * theta2.T
h = sigmoid(z3)
return a1, z2, a2, z3, h
反向传播
def backprop(params, input_size, hidden_size, num_labels, X, y, learning_rate):
m = X.shape[0]
X = np.matrix(X)
y = np.matrix(y)
# reshape the parameter array into parameter matrices for each layer
theta1 = np.matrix(np.reshape(params[:hidden_size * (input_size + 1)], (hidden_size, (input_size + 1))))
theta2 = np.matrix(np.reshape(params[hidden_size * (input_size + 1):], (num_labels, (hidden_size + 1))))
# run the feed-forward pass
a1, z2, a2, z3, h = forward_propagate(X, theta1, theta2)
# initializations
J = 0
delta1 = np.zeros(theta1.shape) # (25, 401)
delta2 = np.zeros(theta2.shape) # (10, 26)
# compute the cost
for i in range(m):
first_term = np.multiply(-y[i,:], np.log(h[i,:]))
second_term = np.multiply((1 - y[i,:]), np.log(1 - h[i,:]))
J += np.sum(first_term - second_term)
J = J / m
# add the cost regularization term
J += (float(learning_rate) / (2 * m)) * (np.sum(np.power(theta1[:,1:], 2)) + np.sum(np.power(theta2[:,1:], 2)))
# perform backpropagation
for t in range(m):
a1t = a1[t,:] # (1, 401)
z2t = z2[t,:] # (1, 25)
a2t = a2[t,:] # (1, 26)
ht = h[t,:] # (1, 10)
yt = y[t,:] # (1, 10)
d3t = ht - yt # (1, 10)
z2t = np.insert(z2t, 0, values=np.ones(1)) # (1, 26)
d2t = np.multiply((theta2.T * d3t.T).T, sigmoid_gradient(z2t)) # (1, 26)
delta1 = delta1 + (d2t[:,1:]).T * a1t
delta2 = delta2 + d3t.T * a2t
delta1 = delta1 / m
delta2 = delta2 / m
# add the gradient regularization term
delta1[:,1:] = delta1[:,1:] + (theta1[:,1:] * learning_rate) / m
delta2[:,1:] = delta2[:,1:] + (theta2[:,1:] * learning_rate) / m
# unravel the gradient matrices into a single array
grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
return J, grad