机器学习实战——朴素贝叶斯
机器学习实战——朴素贝叶斯
思想如下:
有一个物体,具有属性1,2,那么它属于类别A的概率是多少呢?属于类别B的概率又是多少呢?如果属于A的概率大于输入B的概率,那么我们就认为这个物体很可能属于A。这就是朴素贝叶斯概率理论的思想。
思想很简单,目标就是求出一个未知物体的所有属性值对应的各分类的概率。用一个简单的例子表示这个方法:
假设有两个篮子A和B,其中一个篮子A有4000个红色的球和4000个白色的球,另一个篮子B里有1600个红色的球和400个白色的球。现在我们从其中一个篮子里拿出一个球,是红色,那么这个球是从A里拿出来的概率有多少?是从B里拿出来的概率又是多少?
这里涉及到概率论的简单知识:
如果用P(X|Y)表示在条件Y下发生X的概率,那么P(X|Y)=P(XY)/P(Y),上面的例子下,令条件Y为从A篮子取一个球,X条件为拿出一个红色球,那么P(Y)=8000/10000=4/5,P(XY)指同时发生X和Y,很容易计算出来4000/10000=2/5
而P(X|Y)=(2/5)/(4/5)=1/2。
接下来,我们的目标是计算出在发生条件X(拿出一个红球)下条件Y发生的概率,即P(Y|X),从上面的公式可以看出P(Y|X)=P(YX)/P(X)=P(X|Y)P(Y)/P(X),这就是整个算法的核心了,在上面的例子中为(1/2)(4/5)/(5600/10000)。
这里的球色就对应了属性值,而A、B篮子对应的就是类别。
如何计算P(X|Y)、P(Y)、P(X)?
从上面的例子可以看出,P(拿出红球|从A篮子里拿出)=A篮子里红球数/A篮子里的总数(也可以表示为所有球中属于A篮子的数量)。
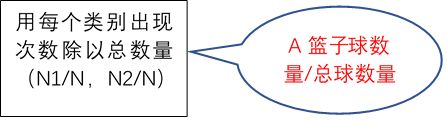
P(Y)=P(A篮子取球)=A篮子里的球数量/总数量
P(X)=P(取红球)=红球的数量/总球数
所以P(Y|X)就可以按上述公式计算出来了。
之所以用如此费劲的描述这么一个简单的例子,是因为接下来会将这个球的例子转换为类别和属性。弄清楚这每部分的计算方式,才能理解属性值概率的计算方法。
用图表表示算法:
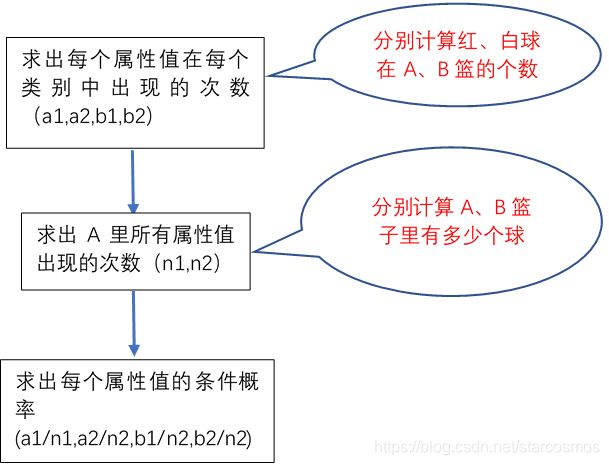
第一步(计算每个属性值对于每个类别的条件概率):
第三步(计算P(X)):
需要注意,这一步在概率比较的时候是不需要计算的,因为样本不变的话,无论拿出来的球是白球还是红球,P(X)都是不会变的,所以比较大小的时候就不用计算这个了。
对训练的样本,把每个属性经过上述方法处理后,就变成了几个概率矩阵,每个矩阵对应了属性值对类别的条件概率。
那么对于遇到的未知类别的物体,其属性x1,x2,x3……,那么求它属于类别A的概率即计算 p(x1)*p(x2)*p(x3)……*p(A),注意,这里之所以可以直接相乘,是假设了所有属性是独立的,这个假设条件也是朴素贝叶斯概率这个“朴素”的来源。如果属性之间有相关性,那么p(x1x2)!=p(x1)*p(x2),就必须计算p(X1X2……Xn),这不在这章的算法中。
在计算中会遇到两个问题,一个是p(Xi)可能是0,那么算出来p(A|X)=0,书中的方法是把Xi出现的次数至少置为1,另外一个问题就是连续的概率(<1)相乘会下溢出从而输出0,这个处理也很简单,取ln之后相加就行了(概率论中的常用处理方法)。
心得总结:
1、 从上面的算法描述就可以看到,属性值必须是有限的,否则无法用次数来计算概率,所以这个算法只适合标称型数据;
2、 书中用words来举例子,用一个words出现与否来作为属性值的0,1计算,如果是一个属性有多个值,此时的计算方法需要稍微处理一下,将每个值出现与否看作是0,1来处理,也就是说,这个算法里其实没有属性,只有值。
3、 这一节中涉及到向RSS提取句子,因为总所周知的原因,书里的网站无法访问,结果我用了个中文网站,才发现中文的词语和英文的word完全不是一个概念,用非字符号分割只能分割成句子,这个问题以后再想想怎么处理。
4、 这个算法一旦建立了样本,每次只需要对输入的物体属性,依次遍历类别数*属性个数次,计算log和乘法,再比较大小,所以耗时很短,比kNN的时间要短很多,而决策树有一个问题就是,对于样本里属性完全一样的情况,决策树没有很好的反应出类别概率的影响(即p(Y)),而是采用叶子结点里的局部高概率,所以有时候决策树结果不如贝叶斯概率。
5、因为之前网络上很多关于酒鬼问题,三门问题之类的争论,其中很多都是因为例子问题导致的,比如这里我用两个篮子来举例,估计会有人说从A篮子和从B篮子取东西概率不是1/2吗?这是例子不当造成的,如果换个说法,这些球放在布上,球上有标记属于A还是B,然后蒙着眼随便抓一个,发现是红球,那么这个红球属于A篮子的概率是多少。这样就可以知道,肯定不是1/2了,因为有A篮子标记的有8000个球,B篮子标记只有2000个。